传动柔性提升机神经网络鲁棒控制及振动抑制

王志刚，朱　畅，郭宇飞

(1.武汉科技大学冶金装备及其控制教育部重点实验室,湖北 武汉,430081；2.武汉科技大学机械传动与制造工程湖北省重点实验室,湖北 武汉,430081)

作为一种常见的垂直运输设备，传统物料提升机质量大、负载/自重比低，一般被视为刚性结构，但实际工作时，其关节铰接和传动链(带)等结构具有一定的柔顺性。这种特性可以对物料装卸时产生的冲击起到缓冲效果，但也会引起关节柔性部位的高频振动。因此，可以将机械臂关节的柔顺特性按Spong模型[1]简化为线性扭(弹)簧，主动引入到物料提升机运动控制研究中，并对柔性关节在运动中产生的高频振动加以抑制，使系统具有更高的控制精度[2-3]。

引入柔性关节特性后的物料提升机刚-柔系统表现出非线性、强耦合等特点[4-5]，采用传统刚性系统的控制方法无法对柔性振动加以抑制，且不能保证系统的稳定性。郭闯强等[6]针对机械臂柔性关节振动问题，设计了基于振动力矩负反馈的PD控制器，可快速抑制振动。Liu等[7]将输入成型理论与反馈线性化结合，采用对基准输入预成型的方法抑制柔性振动。不过，上述控制器虽对机械臂运动中产生的振动加以抑制，却未考虑复杂的外界干扰。Alam等[8]则针对有扰动的单杆柔性臂，基于遗传算法对模糊控制中的比例因子进行调节，设计了混合控制器，削弱了柔性杆运动时末端的振动，但该控制器设计较为复杂，增加了实时控制的难度。

通过奇异摄动法可将适合任意刚性系统的控制器用于柔性系统中，不需要针对柔性系统设计专用控制器，其原理是将刚-柔耦合系统中的刚性轨迹运动与柔性振动通过降阶的方法分解为慢、快两个时变子系统，独立设计控制器，慢变子系统可设计成刚性运动鲁棒控制器，快变子系统则设计成可快速抑制振动的反馈控制器[9]。Aoustin等[10]基于奇异摄动理论设计控制器，实现了两自由度柔性杆机械臂的鲁棒位置控制及振动抑制。陈志勇等[11]采用奇异摄动法，针对柔性关节空间机械臂设计了能对系统参数不确定因素进行补偿的滑模神经网络混合控制器，保证了机械臂控制的精确性。

在上述滑模神经网络控制器中，神经网络起到了对系统误差进行逼近的作用，在不能建立系统准确模型的情况下，RBF神经网络可实时辨识系统的模型误差并进行调整[12]，而且这种基于神经网络设计的修正控制器是整个控制系统的附加部分，可以应用到很多非线性控制系统中[13]。Wang等[14]为克服机器人系统的不确定性和外界干扰，基于RBF神经网络以及Hamilton-Jacobi-Issacs (HJI)不等式设计了一种混合自适应鲁棒跟踪控制器，其中，RBF神经网络即为一种附加控制，其作用是将系统及建模误差视为外界干扰进行在线辨识及逼近，然后通过HJI鲁棒控制器将其衰减到规定范围内，以实现机械臂位置的鲁棒控制。

本文为提高物料提升机位置控制精度与抗冲击能力，将传动链和谐波驱动装置的柔顺特性引入其模型中，并建立整个系统的拉格朗日动力学方程。基于奇异摄动法将系统降阶为快、慢两个时变子系统。慢变子系统采用基于HJI理论和RBF神经网络的鲁棒控制，以实现系统刚性部分轨迹的精确控制；快变子系统则通过速度差值反馈控制器抑制柔性关节的振动。最后通过仿真来验证该混合控制器的有效性。

1　传动柔性物料提升机模型

1.1　结构原理与三维模型

物料提升机结构如图1所示[15]，主要由支架、升降安装板和带料斗的翻转支臂三个部分组成。电机通过链轮带动安装板沿支架上下移动，承载物料的料斗安装在支臂末端，支臂可绕安装板上的旋转轴翻转，其三维模型如图2所示。

图1　物料提升机的结构

图2　物料提升机三维模型

1.2　动力学模型

建立传动柔性物料提升机动力学模型时主要考虑升降和翻转两个部分，其简化模型见图3，其中柔性关节的简化模型见图4。升降部分传动柔性是将传动链简化为具有质心的线性弹簧,等效刚度为k1；翻转部分传动柔性是将谐波驱动装置简化为线性扭簧，转动惯量等效到电机转轴上,等效扭转刚度为k2。建立如图3所示的OXY惯性坐标系,A1为链条等效质量质心，A2和A3分别为升降部分和旋转支臂，支臂长为L。y和yL分别为升降部分位移和链条位移；θ和θL分别为支臂转角和电机轴转角。

图3　传动柔性物料提升机简化模型

Fig.3Simplifiedmodeloftheelevatorwithtransmissionflexibility

图4　柔性关节简化模型

采用拉格朗日方法建模，其动力学方程如下：

(1)

式中:M1为系统正定惯性矩阵；M2=diag(mL,I)为柔性关节惯性矩阵；N为哥氏力、离心力矩阵；G为重力矩阵；K=diag(k1,k2)为柔性关节刚度系数矩阵；q=(y,θ)为系统广义位移；qL=(yL,θL)为传动部分的柔性位移；u=τ1,τ2为驱动力矩向量。

1.3　奇异摄动模型

传动链和谐波驱动装置的关节柔性会引起系统的弹性振动，影响整个系统的稳定性和控制精度，所设计的控制器必须同时满足物料提升机位置控制和柔性关节振动抑制两方面要求。采用奇异摄动法将系统分解为快、慢两个时变子系统：慢变子系统表征系统刚性运动，控制律为us；快变子系统表征系统柔性振动，控制律为uf。因此系统混合控制律如下：

u=us+uf

(2)

(3)

(4)

令ε=0,电机转子与关节之间近似为刚性联接，并将其代入式(4)，可得慢变子变量：

(5)

将上式中的zs代入式(3)中，经化简可得慢变子系统的动力学方程：

(6)

其中H(q)=M1+M2。

(7)

(8)

(9)

式(6)和式(9)即为降阶后的慢、快变子系统的奇异摄动模型。

2　控制器设计

由式(2)可知，完整的系统控制器由快变子系统控制器uf和慢变子系统控制器us组成。前者实现对柔性关节振动的主动抑制，后者实现物料提升机的位置控制。

2.1　快变子系统控制器

将系统传动关节运动速度与柔性关节运动速度的差作为反馈，基于该反馈值设计快变子系统控制器：

(10)

式中：Kf=Kα/ε，其中Kα为正定对角矩阵。系统通过反馈的速度差值调节uf以实现振动抑制和保持系统的稳定性。

2.2　慢变子系统控制器

由于物料提升机工作环境复杂，运输时有不确定的外界干扰，并且装载的物料质量具有可变性，所以精确的物料提升机数学模型难以建立。针对这种情况，本文采用基于HJI理论和RBF神经网络设计的鲁棒控制器[12]，通过神经网络对系统参数误差进行逼近和自适应调整，再通过鲁棒控制器将该误差进行约束，使其降低到规定范围以内，以保证系统能在参数不确定的情况下快速到达期望轨迹。

2.2.1HJI定理

针对如下模型：

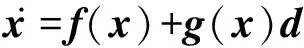
(11)

其中d为外界干扰，设η为系统参数，为了评判系统抗干扰能力，可定义性能指标J：

(12)

2.2.2控制器设计和稳定性证明

在物料提升机动力学方程式(6)中加入系统建模误差，得到方程如下：

(13)

定义期望轨迹为qd，轨迹误差为e=q-qd，设计前馈控制律为：

(14)

式中：T为反馈控制律。

将式(14)代入式(13)，可得闭环系统为：

(15)

Δf=W*Φ+δ

(16)

式中：W*为RBF理想权值；Φ为RBF高斯基函数；δ为逼近误差。

定义

(17)

式中：α>0，为一常数。

将式(13)改写为：

(18)

(19)

针对式(18)所表示的系统，设计自适应调整律为：

(20)

设计系统控制律为：

(21)

式(14)所表示的慢变子系统控制器结构如图5所示：

图5　慢变子系统控制器结构

闭环系统式(15)满足HJI定理，即J≤λ，下面证明系统的稳定性。

定义Lyapunov 函数为:

(22)

由式(18)和式(21)可得:

(23)

定义函数H为

(24)

鉴于:

可得H≤0，再根据式(24)中H的定义，可知：

(25)

式(25)即表明系统稳定。

3　仿真及结果分析

为检验所设计的控制器对传动柔性物料提升机模型的控制有效性，进行两组仿真实验：①通过开、关快变子系统控制器(式(10))，检验柔性关节振动抑制效果以及其对整个系统稳定性的影响；②通过在模型中加入参数不确定性和外界干扰，检验慢变子系统控制器(式(14))的控制精度和鲁棒性。系统模型参数及控制器参数如表1～表2所示。

表1　系统模型参数

表2　控制器参数

选取机械臂初始状态为：

(26)

不失一般性，可选零状态为期望状态，仿真结果如图6～图11所示。

(a) 振动未抑制

(b) 振动抑制

(a) 振动未抑制

(b) 振动抑制

(a) 振动未抑制

(b) 振动抑制

(a) 振动未抑制

(b) 振动抑制

(a) 振动未抑制

(b) 振动抑制

(a) 振动未抑制

(b) 振动抑制

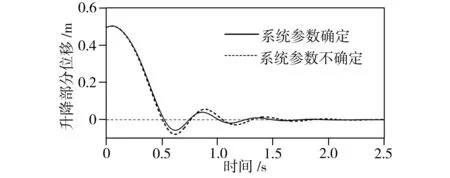
首先，不考虑外界扰动，即采用标称模型。关闭系统的快变子控制器，不对柔性关节振动进行>主动抑制，图6(a)～图11(a)分别为不抑制振动情况下系统的广义位移、速度和控制力矩。从图6(a)和图7(a)可知，系统广义位移轨迹在趋于零状态附近时会呈现出有规律的振荡现象，其振幅相对于整体轨迹较小，但并未收敛。从图8(a)～图11(a)可知，系统的速度响应与控制力矩在运动轨迹趋于零状态的过程中，其振幅不断增大，呈发散趋势，系统处于不稳定状态。这说明柔性关节振动对系统轨迹控制影响较大，使其难以达到期望轨迹。

采用标称模型且开启系统快变子控制器的仿真结果如图6(b)～图11(b)中的实线部分(系统参数确定)所示，与图6(a)～图11(a)对比可知，系统的广义位移、速度和控制力矩的振荡现象在运动初始就得到明显抑制，柔性关节振动控制效果较好，系统广义位移快速到达期望位置，速度趋于零状态点，系统处于稳定状态。为检验控制器应对复杂工况时的控制效果，取系统参数误差为：

并在开启系统快变子控制器的情况下进行仿真，结果如图6(b)～图11(b)中的虚线部分(系统参数不确定)所示，与相应图中实线部分对比可知，当系统参数存在误差时，其系统响应曲线与标称模型的系统响应曲线的变化趋势基本一致，但响应速度稍慢，柔性关节振动同样得到较好抑制。这表明该复合控制器能够克服系统参数误差的影响，可对其进行补偿，且能有效消除因关节柔性而导致的振动，系统状态稳定。

4　结语

为提高物料提升机控制精度和抗冲击能力，本文考虑到传动链和谐波减速装置的传动柔性，将其简化为无惯量线性扭(弹)簧，提出一种传动柔性物料提升机模型，并建立系统拉格朗日动力学方程。

基于奇异摄动理论，将刚-柔耦合模型的控制降阶为轨迹控制和振动抑制两部分。设计了一种自适应RBF神经网络控制器对系统参数误差进行逼近，并通过HJI鲁棒控制器使误差衰减到规定范围内，以实现刚性系统的轨迹控制。对于柔性振动部分，基于柔性传动部件速度差值设计振动抑制控制器。

经仿真验证，所设计的复合控制器能克服未知载荷参数和有界外部干扰的影响，实现系统点对点位置的精确控制，鲁棒性较好，并能对柔性关节振动进行快速抑制，可有效保持整个系统的稳定性。

[1]Spong M W. Modeling and control of elastic joint robots[J]. Journal of Dynamics Systems, Measurement, and Control, 1987, 109(4):310-319.

[2]Tokhi M O, Azad A K M. Flexible robot manipulators: modelling, simulation and control[M]. London: The Institution of Engineering and Technology, 2008.

[3]郭宇飞, 侯保林.传动柔性及负载变化弹药传输机械臂位置控制及柔性振动抑制[J].振动与冲击,2015,34(22):1-8.

[4]Subudhi B, Morris A S. Dynamic modelling, simulation and control of a manipulator with flexible links and joints[J]. Robotics and Autonomous Systems, 2002, 41(4):257-270.

[5]Yu X Y, Chen L. Modeling and observer-based augmented adaptive control of flexible-joint free-floating space manipulators[J]. Acta Astronautica, 2015, 108:146-155.

[6]郭闯强,倪风雷,孙敬颋,等.具有力矩传感器的柔性关节的振动抑制[J].机器人,2011,33(4):449-454.

[7]Liu K P, You W, Li Y C. Combining a feedback linearization approach with input shaping for flexible manipulator control[C]//IEEE International Conference on Machine Learning and Cybernetics, Xi’an, 2-5 Nov. 2003,1:561-565.

[8]Alam M S, Tokhi M O. Hybrid fuzzy logic control with genetic optimisation for a single-link flexible manipulator[J]. Engineering Applications of Artificial Intelligence, 2008, 21(6):858-873.

[9]Siciliano B, Book W J. A singular perturbation approach to control of lightweight flexible manipulators[J]. The International Journal of Robotics Research, 1998,7(4):79-90.

[10] Aoustin Y, Chevallereau C. The singular perturbation control of a two-flexible-link robot[C]//IEEE International Conference on Robotics and Automation, Atlanta, 2-6 May 1993,3:737-742.

[11] 陈志勇,郭益深,陈力.柔性关节双臂空间机器人的滑模神经网络控制[J].系统仿真学报,2014,26(12)：2950-2956.

[12] 刘金琨.RBF神经网络自适应控制MATLAB仿真[M]. 北京：清华大学出版社, 2014.

[13] Choi Y C, Ahn H S. Nonlinear control of quadrotor for point tracking: actual implementation and experimental tests[J]. IEEE/ASME Transactions on Mechatronics, 2015, 20(3):1179-1192.

[14] Wang Yaonan, Sun Wei, Xiang Yangqin, et al. Neural network-based robust tracking control for robots[J]. Intelligent Automation and Soft Computing, 2009, 15(2):211-222.

[15] 姚来鹏,侯保林.基于非奇异终端滑模的物料提升机位置控制[J].农业工程学报,2015,31(12):77-82.