基于梯形模糊相似测度的风险投资多属性群决策方法
陈 雯,平轶男,王 凤,周礼刚
(安徽大学 数学科学学院,安徽 合肥 230601)
多属性群决策是在考虑多个属性的情况下,对已有方案进行排序并选择最优备选方案的一种决策问题,是现代决策科学的重要部分,其理论和方法在工程安全、风险投资、投资管理等方面有着广泛的应用。
现实的研究对象可能是无法明确界定的事物,尤其是在对研究对象进行评价的过程中,存在一定的模糊性和不确定性,因此不能精确地评述或定义事物的真实状况。1965年ZADEH教授提出了模糊集理论[1],用以解决不确定环境下的决策问题。由于研究的对象存在一定的模糊性和不确定性,专家可能会给出一些模糊评价信息,这种评价信息为模糊评价信息的多属性群决策问题,在实际生活中有着重要的理论与应用价值。目前关于模糊多属性群决策方法的研究较多[2-6],也有许多决策方法已应用到现实问题中,如绿色供应商选择[7-8]、物资采购[9]、产品规划[10]等多属性群决策问题。
探索合适的新能源一直是我国近几年所关注的热点,能源已成为国民经济发展的重要支柱之一。不可再生能源将日趋枯竭,探索新能源、可再生能源显得尤为迫切。在我国,可再生能源的研发使用是一个具有巨大发展潜力的产业,同时又在整个现代化过程中起着重要作用。可再生能源项目投资是一项充满高强度综合性、专业性和技术性的活动,同时也是一个具有高投入、高风险和高回报性质的投资产业。这些特征也决定了可再生能源投资所要面临的风险因素十分复杂,风险因素所引起的后果也特别严重。因此作为可再生能源投资者,提高经营管理水平,尤其是进行相关能源项目的投资风险分析已是当务之急。可再生能源投资风险评价就是对将会出现的各种不确性及其可能造成的各种影响和影响程度进行分析和评价。关于可再生能源投资的风险分析具有多属性群决策的典型特征:①影响指标众多;②量纲不统一;③目标冲突;④最优解难以确定。因此采用多属性群决策方法,综合衡量投资风险的影响,成为决策分析的重要问题。
Theil不等系数,最初是作为衡量个人之间或地区间收入差距(或称不平等度)的指标,后来将其运用于度量两组数据的偏差程度,如文献[11]将其应用于组合预测模型中。笔者考虑到Theil不等系数具有的优良性质,基于Theil不等系数提出一种新的梯形模糊相似测度,衡量梯形模糊数之间的偏差,同时考虑决策者的风险态度,在专家权重和属性权重信息完全未知的情况下,基于新的梯形模糊相似测度,构建以梯形模糊相似测度最大化为目标的最优化模型,获取最优专家权重和属性权重,并给出一种基于新的梯形模糊相似测度的风险投资模糊多属性群决策方法。最后笔者对研究结果进行了总结,认为采用该多属性群决策方法进行可再生能源项目风险投资分析,不仅在理论上具有优越性和科学性,在应用中也具有可靠性,为可再生能源的投资风险分析提供了有效方法。
1 基本知识
定义1设X为论域,映射μa:X→[0,1],x→μa(x),确定了X上的模糊集a,则称映射μa为模糊集a的隶属函数,μa(x)称为模糊集a的隶属度。
定义2设论域X为实数集,若a=(aL,aML,aMR,aR),隶属函数μa:X→[0,1]满足:

则称a为梯形模糊数,其中-∞ a⊕b=(aL+bL,aML+bML,aMR+bMR,aR+bR) (1) a⊗b=(aL×bL,aML×bML,aMR×bMR,aR×bR) (2) a/b=(aL/bR,aML/bMR,aMR/bML,aR/bL) (3) 为了比较梯形模糊数的大小,文献[6]和文献[7]定义了梯形模糊数的期望。 (4) (5) (6) (7) 定义4设a=(aL,aML,aMR,aR)为梯形模糊数,则称IL(a),IR(a)分别为a的左期望值和右期望值,分别如式(8)和式(9)所示,称Iε(a)为a的期望值,如式(10)所示,其中,ε为乐观系数,且ε∈[0,1]。若0≤ε<0.5,则表明决策者持悲观态度;若0.5<ε≤1,则表明决策者持乐观态度;若ε=0.5,则表明决策者持中立态度。 (8) (9) Iε(a)=εIL(a)+(1-ε)IR(a) (10) 将式(8)和式(9)代入式(10),则可得: (11) 设a=(aL,aML,aMR,aR),b=(bL,bML,bMR,bR)为两个梯形模糊数,ε为态度参数,则有如下梯形模糊数的大小比较方法: (1)若Iε(a)≥Iε(b),则a≥b; (2)若Iε(a) (12) 则有: (13) 设态度参数为ε,则由式(10)可以得到: 定理2表明,综合模糊矩阵的期望值可表示为所有梯形模糊决策矩阵期望值的加权平均形式,且加权系数为群决策的专家权重。就梯形模糊决策结果而言,期望值具有一定的线性传递性。 由于属性指标在量纲上的不同,存在效益型指标和成本型指标,因此在决策时需对其进行规范化处理。首先给出梯形模糊数的规范化方法: 则效益型梯形模糊属性指标的规范化公式如式(14)所示,成本型梯形模糊属性指标的规范化公式如式(15)所示。 (14) (15) (16) (17) (18) CG公司为一家风险投资公司,现拟开展可再生能源项目的投资。共有4个备选方案可供决策者选择,方案x1为太阳能发电项目,方案x2为风能发电项目,方案x3为生物能供暖项目,方案x4为汐潮能发电项目,组成方案集X={x1,x2,x3,x4},该公司现聘请4位来自能源管理、资本运作、风险管理等相关决策领域的专家参与投资方案的遴选。在遴选的过程中,对每个方案分别从4个属性(U1,U2,U3,U4)进行评价,属性U1为技术性能,即为该项目所依托技术的成熟程度,为效益型属性;属性U2为市场潜力,即为该项目预期的经济效益和社会效益情况,为效益型属性;属性U3为投资风险,即为该项目投资的不确定性,为成本型属性;属性U4为成本分析,即为该项目所涉及产品的成本,为成本型属性。采用的语言评价集为梯形模糊数,决策者并未给出属性和专家的权重向量。 (19) (20) R= (21) 图1 态度参数ε对最优专家权重的影响 图2 态度参数ε对最优属性权重的影响 考虑不同的态度参数ε∈[0,1]对专家权重和属性权重的影响,重新求解式(16)和式(18),得到的结果如图1和图2所示。由图1可以看出,最优专家权重受到态度参数的影响。总体来看,第4个专家的权重随着态度参数的增加始终处于下降趋势,第2个专家的权重始终大于其他3位专家。当ε∈[0.0,0.3]时,随着态度参数的增加,第2个专家和第4个专家的权重逐渐减小,而第1个专家和第3个专家的权重随之增大;当ε∈[0.30,0.35]时,第1个专家的权重小于第4个专家的权重;而当ε>0.35时,第1个专家的权重大于第4个专家的权重;当ε∈[0.9,1.0]时,第3个专家的权重大于第4个专家的权重。根据图2可看出,属性U1和属性U4的权重变化幅度最大。当态度参数ε=0时,属性U1的权重最大,但随着态度参数的增加,属性U1的权重迅速下降;当态度参数ε=0.3时,属性U1的权重接近于0。最初,属性U2、U3和U4的权重十分接近,随着态度参数ε的增加,属性U4的权重迅速上升;当ε<0.16时,属性U4的权重小于属性U1的权重;当ε>0.16时,属性U4的权重大于属性U1的权重,成为权重最大的属性;当ε>0.6时,属性U4成为权重最大的属性,接近于1,与此同时,属性U1、U2和U3的权重接近于0,说明属性U4的重要性比其他3个属性强,也反映了决策者的态度对属性权重的确定有较大影响。 图3 态度参数ε对综合属性值的影响 态度参数对综合属性值的影响结果如图3所示。总体来看,不同的态度参数对最终确定最优方案的影响较大。当ε∈[0.0,0.2]时,最优方案为x3,最劣方案为x1。随着态度参数的增大,方案x1和方案x2的综合属性值迅速增加,同时方案x3和方案x4的综合属性值不断下降。当态度参数ε∈[0.2,0.9]时,最优方案变为x2,最劣方案由方案x1逐渐变为方案x4,当ε∈[0.2,0.4]时,最劣方案为x1,但当ε∈[0.4,1.0],最劣方案变为x4。在态度参数接近于1时,最优方案由x2变为x1。因此,根据上述决策分析,可以看出不同态度的决策者最终选择的最优方案也不同。悲观者更偏向于选择方案x4或者方案x3,态度中立更偏好于方案x2,而乐观的决策者更喜欢方案x1或者方案x2。 与文献[12]相比,同样是在梯形模糊数的背景下提出来的多属性决策方法,但文献[12]在构建理想方案的过程中未考虑决策者的态度,而笔者提出的梯形模糊相似测度,考虑到综合评价值的分散程度及决策者的决策态度,针对不同态度的决策者有着不同的选择方案。另外,文献[13]利用模糊理想解和广义加权距离构建模型,通过Borda记分法给出最优方案,虽然不用给出属性权重和专家权重,但也未能考虑专家和属性的相关信息,笔者提出的方法充分考虑专家权重和属性权重信息,并且是基于决策者的态度给出的,对方案的选择有着较大影响,也更符合实际情况。 笔者在梯形模糊信息环境下,考虑专家权重和属性权重均未知的情况,定义了一种新的梯形模糊相似测度,研究了其优良性质,考虑决策者的决策态度,构建了基于梯形模糊相似测度的专家权重和属性权重确定模型,提出了基于新的梯形模糊相似测度的模糊多属性群决策方法,最后通过案例分析说明了该方法的可行性和有效性。在未来的研究中,越来越多的信息将会以模糊数的形式给出,笔者提出的方法可以进一步应用在其他模糊语言环境中,如区间二元语义、直觉梯形模糊数[14-16]等。另外,也可将笔者提出的方法应用于实际问题中,如选址问题、供应商的产品选择问题等。 参考文献: [1]ZADEH L A. The concept of a linguistic variable and its application to approximate reasoning [J]. Information Sciences, 1975,9(1):43-80. [2]吴群,吴澎,周元元,等.2TLCGPOWA算子及其在多属性群决策中的应用[J]. 计算机工程与应用,2017,53(3):47-53. [3]吴群,吴澎,周礼刚.基于联系数的区间二元语义模糊多属性群决策方法[J].重庆工商大学学报(自然科学版),2016,33(1):1-8. [4]万树平,董九英.多属性群决策的直觉梯形模糊数法[J].控制与决策,2010,25(5):773-776. [5]徐泽水.不确定多属性决策方法及应用[M].北京:清华大学出版社,2004:237-241. [6]刘培德,张新.直觉不确定语言集成算子及在群决策中的应用[J].系统工程理论与实践,2012,32(12):2704-2711. [7]QIN J D, LIU X W, PEDRYCZ W. An extended TODIM multi-criteria group decision making method for green supplier selection in interval type-2 fuzzy environment [J]. European Journal of Operational Research,2016,258(2):626-638. [8]吴坚,曹清玮.不确定决策环境下绿色供应商选择方法研究[J].运筹与管理,2012,21(1):220-225. [9]董鹏,罗朝晖,刘刚.基于OWA算子的物资采购评标定标决策研究[J].武汉理工大学学报(信息与管理工程版),2007,29(7):92-95. [10]邱方鹏,莫莉.基于直觉模糊集的产品规划评估群决策研究[J].武汉理工大学学报(信息与管理工程版),2013,35(5):723-727. [11]周礼刚,陈华友,丁子千,等. 基于Theil不等系数的IOWGA算子组合预测模型[J].安徽大学学报(自然科学版),2010,34(1):1-6. [12]刘於勋,沈轶,谢妞妞.基于梯形模糊数期望值的多维偏好群决策模型[J].控制与决策,2009,24(9):1377-1379. [13]陈业华,黄元美.基于梯形模糊数的多维偏好群决策模型[J].燕山大学学报,2005,29(6):535-539. [14]彭旭,韩冰,陈华友.基于可能点的TOPSIS 模糊多属性决策方法[J].武汉理工大学学报(信息与管理工程版),2015,37(6):761-770. [15]周佳敏,王展青.基于三角模糊数的动态混合多属性决策法[J].武汉理工大学学报(信息与管理工程版),2014,36(1):121-129. [16]吴群,王凤,周礼刚,等.基于区间二元语义偏好关系一致性偏差的群决策方法[J].模糊系统与数学,2017,31(5):55-67.
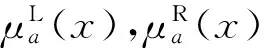
2 梯形模糊相似测度









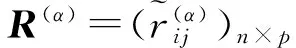
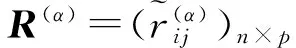

3 基于梯形模糊相似测度的模糊多属性群决策方法


3.1 基于梯形模糊相似测度的专家权重确定模型

3.2 基于梯形模糊相似测度的属性权重确定模型


3.3 基于梯形模糊相似测度的模糊多属性群决策方法

4 案例分析





5 结论

