考虑货物类别的电动汽车路径优化问题研究
张艳伟,黄志红
(武汉理工大学 物流工程学院,湖北 武汉 430063)
电动汽车依靠车载电池提供动力,能够有效减少尾气污染,节约环境治理成本,这一特点促使其在物流配送行业中得到广泛的关注与应用[1]。电动汽车产业和配套服务设施的快速发展为电动汽车在物流配送行业的普及提供了有力保障。然而,电动汽车最大行驶距离受到电池容量的限制。此外,由于货物性质和配送条件的差异,现实中普遍存在着部分类别的货物不能与指定类别货物在同一车厢中混合运输的情况,而这些货物本身可以和除开指定类别以外的大多数种类的货物一起配送。主要原因有:①配送条件不同。如土豆和红薯在运输过程中适宜的温度不同,红薯喜温,温度适合在15 ℃以上,否则就会僵心;土豆喜凉,温度适合在2~4 ℃,否则就会发芽。②货物性质不同。如茶叶不能与糖一同配送,这两类物品放在一起会导致茶叶吸收潮湿而发霉。此外茶叶等具有吸附性的货物不能和樟脑丸、香皂、香水、香烟等具有异味的货物装在同一车厢内。③其他原因。如未出栏的育肥猪不宜和用于产崽的母猪共同运输,运输会使猪产生应激反应。体重差异过大可能导致小猪被大猪压死或踩伤。这就产生了带有货物类别约束的车辆路径问题(vehicle routing problem,VRP)。货物类别和运输路径是相互制约的,忽略货物类别的差异性可能增加货物在运输途中的损失,降低对顾客的服务水平。忽略运输路径的优化,更多的配送车辆和更长的配送距离又将产生高昂的运输成本。只有兼顾两方面的约束,才可能实现问题的全局优化。这也对车辆路径问题提出了更高要求。因此,科学地规划电动汽车配送路径,优化电动汽车物流网络成为近期的研究热点问题。
近年来,国内外学者从多方面对电动汽车路径优化问题进行了研究,取得了丰富的成果。王征等[2]建立起带二维装箱约束的物流配送车辆路径模型,提出了解决该问题的启发式算法Memetic。王长琼等[3]研究了三维装载约束下的汽车零部件循环取货路径优化问题,在循环取货过程中考虑实际车辆路径约束和三维装载约束条件,构建了三维装载约束下零部件循环取货路径优化模型,提出了一种混合禁忌算法求解该问题。YANG等[4]研究了电动汽车物流配送系统配送路径优化问题,考虑了配送车辆的最大载重量及电动汽车每次充满电的最大行驶里程。揭婉晨等[5]研究了含时间窗的多车型电动汽车车辆路径问题,考虑配送车辆不同的载重量和最大行驶里程。王胜等[6-7]采用改进混合启发式算法对车辆路径问题进行了研究。BORTFELDT等[8]将车辆路径问题与车辆装载问题进行整合优化,并在路径优化中考虑车辆装载体积和质量约束.
综合来看,多数研究车辆路径问题的文献大多关注于路径长度的最小化,仅将货物重量纳入考虑范围。考虑了货物属性的文献也仅仅关注于货物形状,没有根据货物配送要求与条件将货物分类配送。鉴于此,笔者建立基于电动汽车运营成本最小化的考虑货物分类配送的电动汽车车辆路径决策模型, 与已有研究的主要区别为:①除了重量外,赋予货物配送属性参数。货物仅能和与其属性相同或相近的货物共同配送;②提出了MCWS和MHGA两种启发式算法来解决该问题,并对两种算法的求解性能进行比较。
1 问题描述及数学模型
1.1 问题描述
物流配送网络G=(V,E),其中V={v1,v2,…,vn}表示顶点集合,由顾客集合I、配送中心o和虚拟配送中心o′ 共同组成,即V=I∪{o}∪{o′}。E={(vi,vj):vi,vj∈V,vi≠vj}表示弧的集合。集合I中每个节点i都具有需求量参数qi和分类参数ci。将货物分为A,B,C 类,对应的分类参数分别为-1,0,1,其中A类货物可以和B类货物共同配送,B类和C类也可以共同配送,但是A类货物和C类货物不可以共同配送。集合E中每条弧都包含非负权值属性dij,dij表示节点i和j之间的距离。K={k}表示配送车辆集合。集合K中每一辆车k都包含两个非负权值属性,即车辆k的最大载重Uk和满电量状态下最长行驶里程Q。集合R={r1,r2,…,rz}是配送路径的集合,每条路径由一辆车负责配送。pik为车辆k到达节点i的电量还能行驶的距离;uik为车辆k离开节点i时的剩余载重量;qi为节点i处顾客的需求量;γ为车辆行驶单位距离的单位成本;xijk为0-1变量,当车辆k经过弧(i,j) 时,xijk=1,否则为0。
1.2 数学模型
基于上述条件,构建如下数学模型:
(1)
s.t.
∀j∈I
(2)
(3)
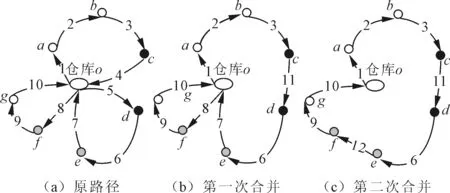
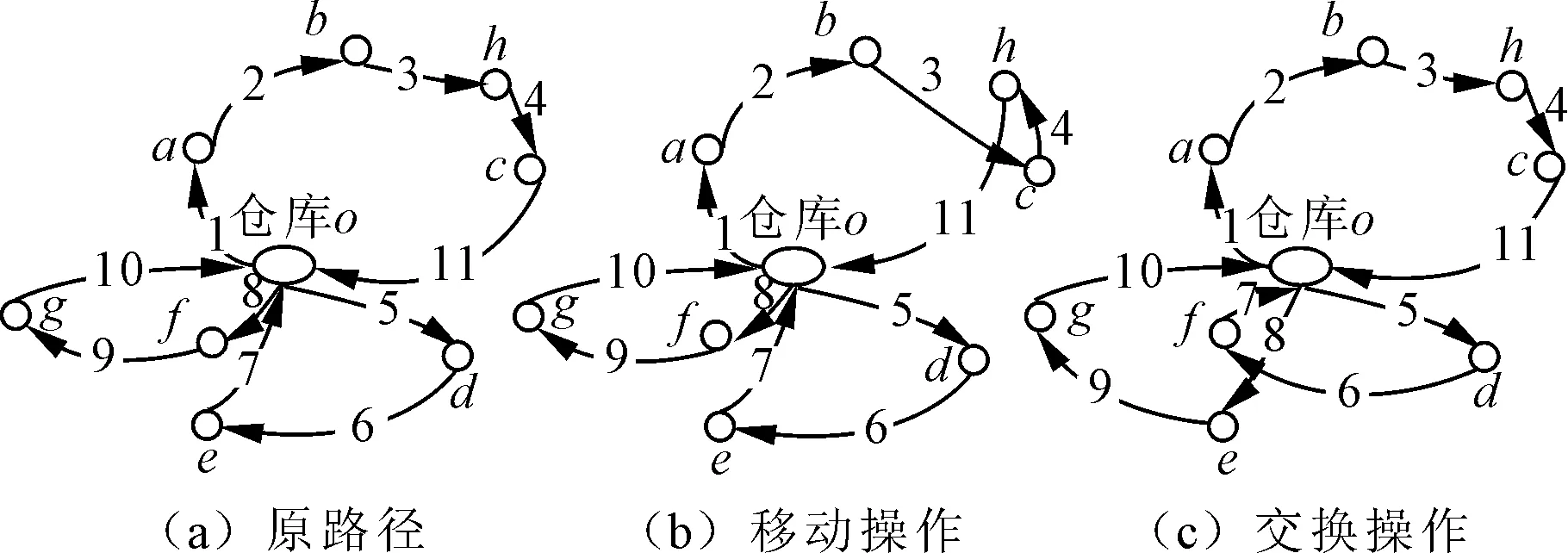
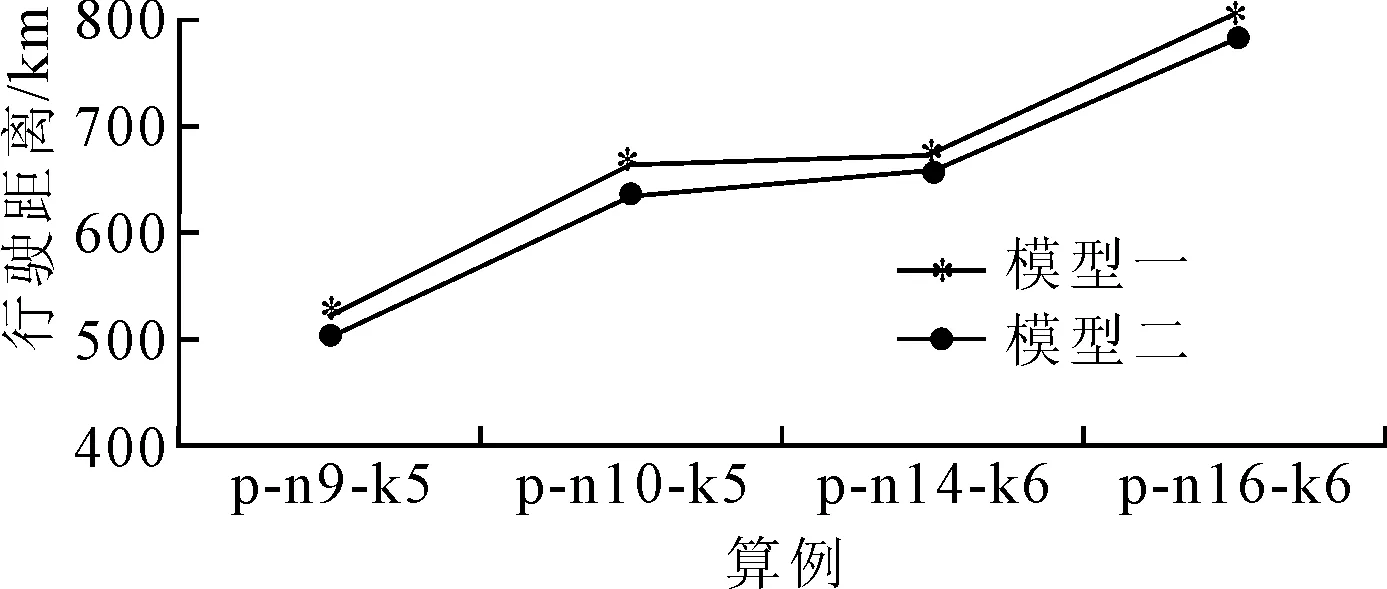
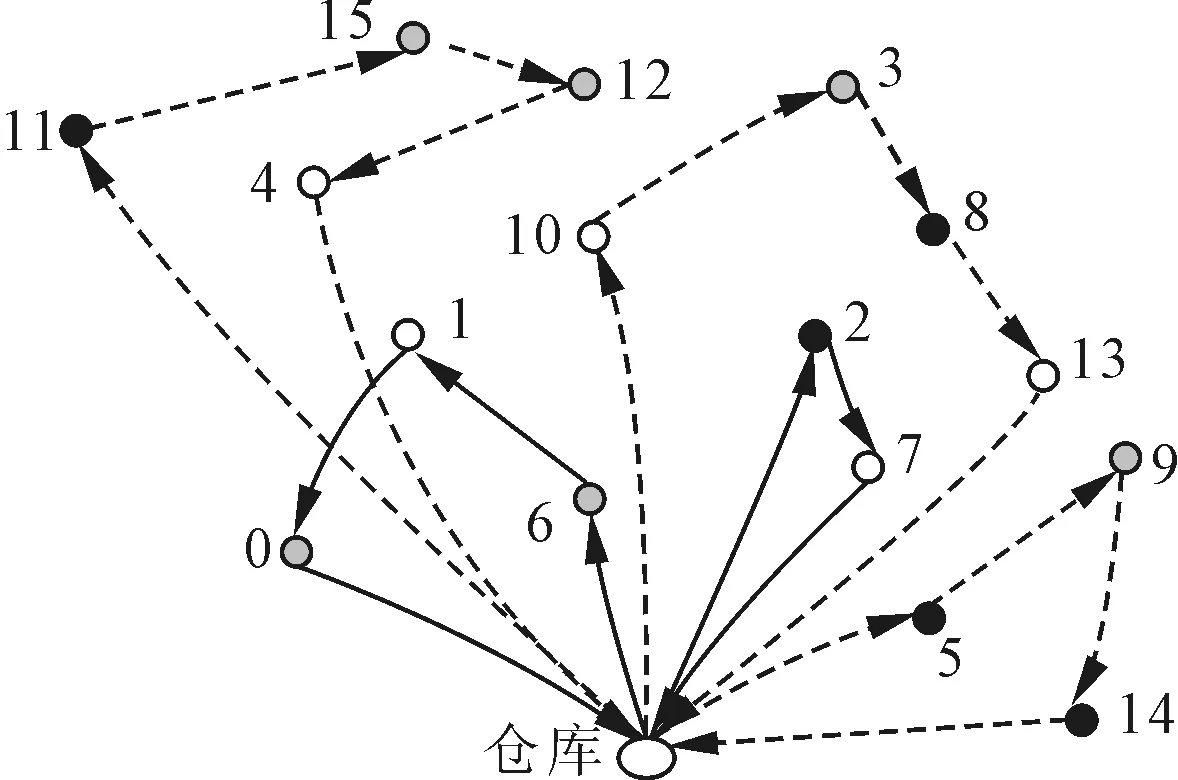
∀i∈V (4) (5) (6) ujk≤uik-qjxijk+Uk(1-xijk) (7) ∀j∈V uok≤Uk∀k∈K (8) ujk≥0∀k∈K,j∈V (9) (10) ∀j∈V pjk≤pik-dijxijk+Q(1-xijk) (11) ∀i∈V pok=Q∀k∈K (12) pjk≥0∀j∈V (13) xijk∈{0,1}∀i∈V (14) 上述模型中,式(1)表示最小化运营成本;式(2)表示每个顾客点只被服务一次;式(3)表示各点车流量平衡;式(4)表示配送车辆从仓库出发,服务若干顾客点后最终回到原来的出发点;式(5)表示每辆车最多服务一条路径;式(6)表示参与配送任务的车辆数目不能超过拥有的车辆总数;式(7)表示配送车辆按照路径途经各点的剩余货物量。如果车辆k在经过顾客点i后直接到达顾客点j(即xijk=1),则车辆离开j点时剩余货物量等于离开i点时的剩余货物量减去j点的需求量,否则,式(7)被松弛;式(8)确保任何一条路径中的顾客总需求量不能超过提供服务的车辆的最大载重量;式(9)表示剩余货物量为非负;式(10)表示只有属性相同或相近的货物才能由一辆车配送;式(11)表示配送车辆按照路径途经各点的剩余电量,逻辑关系类似于式(7);式(12)表示车辆离开起点时的电量;式(13)表示充电量为非负数;式(14) 表示变量属性。 Clarke-Wright节约算法是一种求解车辆路径问题的经典启发式算法,ERDOAN等[9]对算法进行改进以解决电动汽车车辆路径问题(GVRP)。笔者采用启发式算法MCWS(modified Clarke-Wright savings heuristic)求解区分货物类别的电动汽车配送路径问题,具体步骤为:①为每个需要服务的顾客点i生成一条对应的路径(o-i-o),其中点o为配送中心。②查找出可行路径中与点o相连的毗邻点,计算任意连接不同路径上两个毗邻点的saving值,将毗邻点以成对的形式按照saving值降序排列放入节省对列表SPL中,saving=doj+doi-dij。③将SPL节省对按照saving值降序顺序执行路径合并。如果两个毗邻点不属于同一条路径,两条对应路径的需求点之和小于车辆的载重限制,且货物类别可以同时配送,则将两个点所在的路径合并。合并方法如下: 删除毗邻点与点o之间的连接线,随后将两个毗邻点直接相连。合并后检查新路径是否满足电动汽车行驶路径的电量约束。如果不满足,则放弃此次路径合并。两路径合并流程如图1所示。④将SPL中所有毗邻点对合并之后,返回步骤①进入新一轮路径合并,直到任意两条可行路径都不能进一步合并为止。⑤为了提高解的质量,笔者采用移动和交换两种形式进一步优化当前解。移动是指移动路径中某一顾客点的位置,将其与同路径中其余所有顾客点依次互换位置。交换是指交换不同路径中两个顾客点的位置。以上两种策略均采用穷举法实现,优化过程需满足车辆行驶里程和载重量约束。路径优化流程如图2所示。 图1 两路径合并流程 图2 路径优化流程 遗传算法是一种借鉴自然选择和自然遗传机制的随机化搜索方法,其全局搜索能力较强而局部搜索能力不足。爬山算法是一种基于邻域搜索技术的,沿着有可能改进解的质量的方向进行单方向搜索(爬山)的方法,其具有较强的局部搜索能力。笔者将遗传算法与爬山算法相结合,为弥补遗传算法局部搜索能力的缺陷,采用改进混合遗传算法MHGA(modified hybrid genetic algorithm)求解区分货物类别的电动汽车配送路径问题。重点需要考虑以下几个问题: (1)编码方案。笔者使用顾客自身排列的编码方法来确定配送路径策略。该方法直接生成N个1~N间不重复的整数的排列,每个自然数表示一个顾客个体。例如一条染色体为(7,4,1,3,6,5,2),则表示等待服务的顾客点顺序为(N7,N4,N1,N3,N6,N5,N2)。根据排列中数字的顺序,依次指派给配送车辆,满足以下3个条件之一,则由对应顾客点开始将其指派给下一辆配送车辆:①配送路径长度超过车辆一次配送的最大行驶距离;②当前货物类别不能与之前已指派给该车辆的配送货物类别一起配送;③顾客的需求量之和超过车辆最大载重量。如果顾客需求的配送路径数多于可使用的配送车辆数目,则该个体对应一个不可行解。 (2)群体初始化。假设群体规模为M,则采用随机生成的方式得到M个不同个体,每个个体包含N个1~N间不重复的整数的排列。 (4)选择操作。将每代群体中适应度最高的个体复制后放入下一代第1列,其余个体根据适应度大小,在轮盘赌机制下以一定概率进入下一代。 (5)交叉操作。由于笔者采用了序号编码方式,不能像非序号编码的染色体一样任意进行交叉。采用PMX类型交叉算法,交换个体交叉点之间的片段。如果新生成的基因序号没有出现冲突则保留此个体,否则通过部分映射确定新个体。PMX交叉的过程如图3所示。 图3 PMX交叉的过程 (6)变异操作。序号编码下基因突变的常见方式有两种:①互联变异,即在变异的个体中随机选择两个基因并交换其位置,从而形成一个新的子代个体;②逆转变异,即在变异的子个体中随机选择两点,将两点之间的基因进行逆转。笔者交替使用两种变异技术保持群体内个体的多样性。 (7)爬山操作。针对遗传产生的每一代中的最优个体,随机交换其中两个基因的位置。如果交换基因位置后个体的适应度增加,则保留新个体放弃原个体。否则继续交换到指定次数为止。 (8)终止准则。笔者采用进化指定代数的终止准则。 实验的计算机参数配置为Intel(R) I5-4460,3.20GHz,8GB RAM。算法在JAVA中实现为单线程代码。 数据来源主要包括两部分:benchmark 采用AUGERAT等[10]提出的算例,可以从网站http://neo.lcc.uma.es/vrp/vrp-instances/上获取。算法使用参数来源于文献[4]和文献[11]。 4.2.1模型与算法的验证分析 为了评估模型的准确性及算法的寻优能力,笔者使用能被IBM ILOG CPLEX12.6求解的小规模算例进行计算。随后与混合遗传算法和改进节约算法的计算结果进行比较。为了保证实验的一般性,在文献[8]提出的算例P-n16-k8中选择6组小实例数据,小实例数据只选用了初始算例的最后n个顾客点。每组实例包含的顾客数与可用车辆数目不同。设定CPLEX运行时间的上限为3 600 s。*表示此解是CPLEX运行3 600 s得到的可行解。#表示CPLEX未能在规定时间内找到可行解。考虑到算法中包含随机参数,针对每一个算例都将算法运行10次,实验结果对比如表1所示。其中N和K分别为算例包含的顾客点数目和可调配的车辆数。S表示配送路径数目;Time表示求解时间;Gap表示算法最优解与CPLEX结果的相对差值,Gap=(算法的最优解-CPLEX求出的最优解)/CPLEX求出的最优解。通过表1可以看出启发式算法的结果与CPLEX非常接近,并且算法求解效率较高,验证了模型和算法的正确性。 4.2.2模型对运营成本的影响性分析 笔者将所提出的考虑货物分类的VRP模与传统VRP模型进行对比研究,从文献[8]的数据集中选取4组实例,比较算例在两种数学模型下的最优运营成本。 表1 实验结果对比 图4 配送距离对比 图5 混运路径数量对比 两种模型在不同案例中配送距离对比情况如图4所示。其中,模型一表示已区分货物类别,模型二表示未区分货物类别。由图4可知,两种模型在不同算例中的行驶距离非常接近,模型二的距离略短于模型一。两种模型在不同案例中将不适宜共同配送的货物指派给同一辆车的混运配送路径数量如图5所示。其中,模型一在建模之时区分了货物类别,避免了以上情况的发生,所以在4组算例中的结果均为0。模型一可以在总路径略微增加的情况下,通过改变路径策略来减少混合配送的路径,以降低货物在配送过程中的损失,提高顾客满意度。 笔者以算例p-n16-k6为例,展示两种模型求解出的最优路径策略。算例p-n16-k6包括16个顾客点,最大可使用车辆数为6辆。图6和图7分别展示了模型一和模型二的路径策略,图中黑、白、灰3色圆圈表示顾客需求货物类型分别为A、B、C,其中A、C两类货物不适宜由同一辆车混装配送。路径策略如表2所示。由表2可知,两种模型在该算例中都只使用了5辆配送车辆。*表示此路径中A、C两类货物由一辆车配送。其中,模型一的路径总长度为800.48 km。模型二的路径总长度为783.93 km。 图6 模型一配送路径图 图7 模型二配送路径图 序号模型一配送路径模型二配送路径1仓库→8→13→7→仓库仓库→2→7→仓库2仓库→0→15→12→3→9→仓库仓库→6→1→0→仓库3仓库→11→4→10→1→仓库仓库→10→3→8→13→仓库*4仓库→14→5→2→仓库仓库→11→12→15→4→仓库*5仓库→6→仓库仓库→5→9→14→仓库*路径总长/km800.48783.93 4.2.3算法寻优能力的对比分析 笔者采用9组不同规模算例验证两种算法的路径优化能力。算法运行10次并将最优解记录下来,实验结果对比如表3所示。其中,J表示算法最优解使用车辆数目。由表3可知,两种算法最优解的相对差距最大达到了11.842%。通过比较可以看出,MCWS 的解整体优于MHGA,MHGA只在算例p-n55-k20中得到了最优值。此外,实验结果显示对不同的算例,算法的求解时间大相径庭,同类型实例的求解时间随着模型规模的增加呈现出上升趋势。规模相近的不同类型实例的求解时间也有较大差异。这表明算法的性能同时受到问题规模和数据自身特性的影响。总体来说,计算时间在企业可接受的时间范围内,不影响算法的一般实用性。 表3 实验结果对比 笔者在电动汽车配送车辆路径问题的基础上引入了一个重要概念,即配送货物的混装类别。将货物的组合特性纳入考虑范围并建立了线性规划数学模型,统筹安排车辆的行驶路径使得物流企业在运营成本没有明显增加的前提下可以降低货物运输损失,提高服务质量。此外,还设计了两种求解该问题的改进型算法MCWS和MHGA,将算法在文献[8]的小规模算例上跟CPLEX 进行比较,取得了较好的结果。随后采用多组算例比较两种模型下的运营成本。实验结果表明,考虑混装货物类别的模型可以在略微增加配送距离的情况下,避免将不适宜混装在一个车厢内的货物指派给同一车辆配送,达到降低货物运输损失,提高顾客满意度的目的。最后,将两种算法在较大规模算例上进行实验对比。实验结果表明,MCWS 算法对于GVRP问题有着较好的寻优能力,而且具有较强的稳定性,提升了该问题理论成果的实用性。 但是,笔者研究中没有考虑电动汽车在途充电问题,且算法效率还有提升空间,如何设计更加高效的算子将是未来工作的一个重点。 参考文献: [1]CHELLASWAMY C,RAMESH R,RAU C V. A supervisory control of a fuel free electric vehicle for green environment[C]∥Emerging Trends in Electrical Engineering and Energy Management(ICETEEEM).Chennai: IEEE,2012:387-393. 哺乳期仔猪出现呕吐、腹泻症状,随后排出黄白色粥样稀便,卧地不起,强迫仔猪站立,仔猪行走时左右摇摆,行走不稳,不能正常吃乳,仔细观察发病猪四肢内侧存在紫色点状出血,发病猪腹泻物中夹杂不完全的白色凝乳块。随着病情进一步发展,腹泻症状严重,患病猪身体逐渐消瘦,不能正常行走,行走时左右摇晃,共济失调,四肢叉开,口吐白沫,叫声嘶哑,耳部和腹部皮肤表面发红,并出现绿豆大小的蓝紫色出血点。多数患病猪在发病中后期,排出黄色或黄褐色粥样稀便,病猪在临死前表现角弓反张,全身肌肉震颤,出现间歇性痉挛,后期肢体麻痹,呈现犬坐姿势,有时在圈舍中转圈或者侧卧时四肢划动呈游泳状,最后因机体衰竭而死。 [2]王征,胡祥培,王旭坪.带二维装箱约束的物流配送车辆路径问题[J].系统工程理论与实践,2011,31(12):2328-2341. [3]王长琼,戚小振.三维装载约束下的汽车零部件循环取货路径优化研究[J].武汉理工大学学报(交通科学与工程版),2015,39(6):1161-1165. [4]YANG J,SUN H. Battery swap station location-routing problem with capacitated electric vehicles[J]. Computers & Operations Research,2015(55):217-232. [5]揭婉晨,杨珺,杨超.多车型电动汽车车辆路径问题的分支定价算法研究[J].系统工程理论与实践,2016,36(7):1795-1805. [6]王胜,谭家政,刘勇,等.求解TSP问题的改进蚁群算法[J].武汉理工大学学报(信息与管理工程版),2013,35(3):340-344. [7]张艳伟,周万,向家伟.基于运输网络的配送路线优化模型[J].武汉理工大学学报(信息与管理工程版),2014,36(4):447-451. [8]BORTFELDT A,HOMBERGER J R. Packing first,routing second:a heuristic for the vehicle routing and loading problem[J]. Computers & Operations Research,2013,40(3):873-885. [9]ERDOAN S,MILLER H E. A green vehicle routing problem[J]. Transportation Research Part E: Logistics and Transportation Review,2012,48(1):100-114. [10]AUGERAT P,BELENGUER J M,BENAVENT E,et al. Computational results with a branch and cut code for the capacitated vehicle routing problem[J]. Rapport De Recherche- IMAG,1995(12):495. [11]张瑞锋,汪同三.新型遗传算法求解车辆路径问题研究[J].湖北大学学报(自然科学版),2013,42(2):120-123.

2 启发式算法MCWS
3 启发式算法MHGA

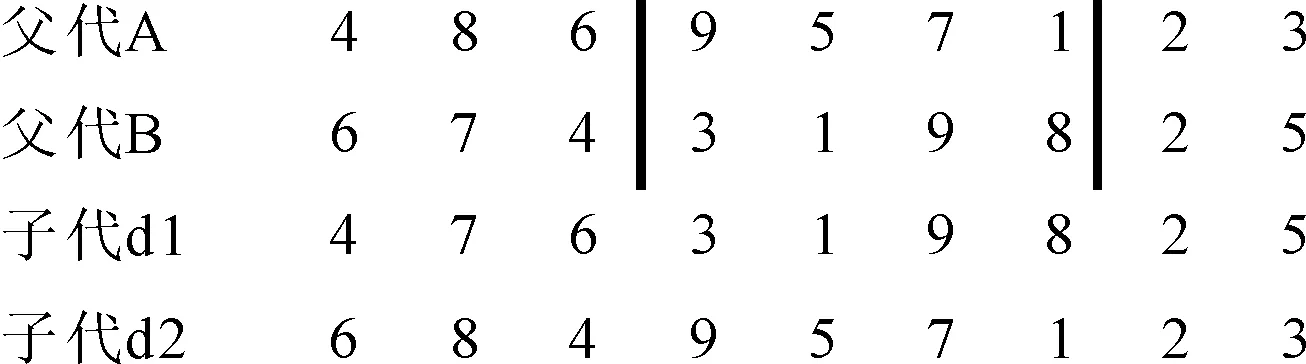
4 实验结果及分析
4.1 测试用例
4.2 实验结果与分析





5 结论

