带时间窗的危险品运输道路网络设计

刘苗苗，韩晓龙

(上海海事大学 物流研究中心，上海 201306)

危险品是易燃易爆有剧烈腐蚀性物品的统称，危险品运输通常由专门组织或者技术人员对非常规物品采用特殊车辆进行运输并经过国家相关职能部门严格审核，因此在危险品运输的研究问题中政府监管部门是上层决策者。由于危险品特殊的属性，危险品运输过程中一旦发生事故且得不到及时的控制，会严重威胁周边人群的财产、生命安全，破坏生态环境。随着我国化工产业的发展，危险品道路运输显著增多，如何降低危险品运输过程中的事故风险越来越为公众所关注，而危险品运输网络设计是一种有效的途径。

现有国内外的文献对危险品运输道路的研究大部分集中在路径优化、风险评估及应急等方面，而关于危险品运输网络设计的文献比较少。LIST等[1]对有害物质(危险品)道路运输风险评价和运输路线选择进行了系统的分析。REN等[2]提出并分析了易燃易爆危险品道路运输的应急响应等级模式。MAHMOUDABADI等[3-4]主要运用混沌迭代过程理论，基于不同风险属性的优先级确定目标函数，建立危险品路径选择模型。于建平等[5]在一般双层规划求解的基础上运用了双层遗传算法求解双层问题。李昌兵等[6]针对非线性双层问题，提出了基于层次粒子群算法的求解策略。KARA等[7]最早提出了双目标-双层模型，并使用库恩-塔克条件和线性化补充松驰条件代替下层规划，将双层整数规划模型转化为单层的混合整数规划模型进行求解。ERHAN[8]将危险品运输网络设计问题描述成Steiner树问题，并使用加权求和的方式来最小化网络总运输风险和成本。储庆中等[9]初次将遗传算法用于危险品道路运输路径网络设计中。蒋洋[10]采用粒子群算法对危险品运输网络设计问题进行求解。张丽娜[11]在一般危险品运输网络双层规划模型的基础上建立双层多目标模型，提出了特定的危险品在特定路段采取征收费用的危险品运输路径网络设计，并借鉴启发式算法进行求解，但是在模型中上层决策者没有兼顾运输企业运输成本最小化的目标且仅针对一类危险品。

笔者在兼顾政府监管部门和运输企业的基础上，建立了基于不同危险品特定路段征收特定费用的模型，且在一般网络设计模型的基础上考虑时间成本，并用Lingo进行求解。

1　危险品运输网络设计分析

在危险品运输道路网络设计中,通常是考虑一个拥有一定数量的起点和终点(目的地)的城市道路网络。当然,对于多个城市之间的运输网络的设计也同样适用。危险品运输网络有两个决策体：政府监管部门和运输企业，当地政府监管部门指定运输网络，运输企业在指定的网络中选择运输路线。因此科学的危险品运输道路网络设计应是上层决策者(政府监管部门)实现决策中主要目的即风险最小化,同时也应考虑运输企业成本最小化的路径选择行为；而运输企业在上层决策的基础上选择运输路线，是实现主要目的成本最小化。这种情况构成了双层设计问题,政府监管部门代表第一层，运输企业代表第二层。基于此,笔者针对不同种类危险品，提出了带时间窗的危险品运输道路网络设计问题。

2　危险品运输网络双层规划模型

用有向图G=(V,A)代表现有的道路运输网络，节点集合用V表示，节点代表道路交叉口;路段集合用A表示，一条边代表一个路段。有m种危险品通过网络G=(V,A)自起点o∈N到终点d∈N进行运输，该网络设计问题是在G上寻找一个包含k个运输任务的网络，运输企业以成本最小为原则选择线路，政府监管部门以期望的总风险最小为原则选择线路。每个运输任务对应一对起讫点。用(i,j)表示路段，点i、j∈V,(i,j)∈A。o(k)、d(k)表示第k个任务的OD，k∈{1,2，…,K}，点o,d∈V。

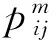
在此基础上建立了改进后的带时间窗的危险品运输道路网络0-1模型，式(1)为上层规划目标函数,表示政府期望网络总风险最小；式(2)表示任何一种危险品经过任何一条路段所征收的费用为正数；式(3)表示政府监管部门在每条路段上的风险期望限制,防止路段风险超过允许风险上限；式(4)表示上层决策变量的0,1约束。

(1)

(2)

(3)

(4)

下层数学模型中，式(5)为下层目标函数, 表示运输者期望的总运输成本最小，通过对不同的危险品及路段设置不同的通行费用使危险暴露人口与运输成本达到综合最小化,实现期望运输成本和风险损失最小；式(6)表示运输网络实现流量均衡, 保证货物运出和到达目的地；式(7)表示运输企业只能在政府监管部门开放的路段中选择路线；式(8)表示下层决策变量的0,1约束。

(5)

∀j∈V,k∈{1,2,…，K}

(6)

(7)

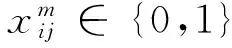
(8)

双层规划问题通常是一个NP-hard问题。笔者建立的模型是一个混合整数线性规划(MILP)，可直接利用Lingo软件进行求解，确定科学的危险品运输道路网络。

3　算例分析

假设某一地区有一既定的网络图，如图1所示。为简化计算，假设所有运输任务的期望事故影响后果和期望经济承担相同，每个运输任务的时间窗已知，各运输任务运输车辆均为1辆。每条路段的影响后果C用影响范围内的暴露人口数量表示，每条路段的单位运输成本如表1所示。为了阻止运输企业选择风险较大的路段(3，4)和(6，5)，政府在路段(3，4)征收1个单位的通行费，在路段(6，5)征收2个单位的通行费。

图1　运输网络

路段(1,2)(2,3)(2,6)(3,4)(3,5)(7,6)(6,5)(6,8)(5,4)(5,9)事故影响后果/万人1114115111运输成本/万元1113311111

假设该运输网络中有3个运输任务(K1:2→4,K2:7→9,K3:1→8)，并且规定了每个任务的时间窗及相应的惩罚成本，具体数据信息如表2所示。通过Lingo求解得到: 总的期望损失R=3, 总的运输成本C=100。政府及运输企业的决策如表3所示。

由表3可以看出，对于任务2→4，在政府对路段(3,4)征收1个单位通行费，对路段(6,5)征收2个单位通行费的限制条件下，运输企业选择的最优路径为2→3→5→4，求解的总风险R=3，总成本C=100;任务1→8和7→9都只有一条可通行的路径，分别为7→6→5→9和1→2→6→8。

如果采用一般的网络设计方法(政府监管部门对于风险较大路段禁止通行)和政府对运输企业不进行管制(即运输企业以成本最小化为目标可在既定道路网络上自由选择),求解得到运输企业在3种策略下的最优路径结果，如表4所示。

表2　运输任务及相关数据

表3　政府及运输企业的最终决策

表4　3种策略下的最优路径结果对比分析

从表4可以看出通过3种网络方案设计比较，笔者所建立的到时间窗危险品运输网络双层规划模型，通过对特定的危险品在特定路段征服收通行费的策略可以有效协调风险和成本。

通过设置路段通行费，可以阻止一部分运输企业使用此路段，而其他运输同种危险品的运输企业依然可以选择此路段。但一般的网络设计方法就没有这种灵活性，所有运输同种危险品的运输企业的路径都是一样的。因此可以说特定路段设置高额通行费策略比一般的网络设计要好。

4　结论

笔者建立了带时间窗的危险品运输双层规划模型，通过对特定路段收取通行费有效协调运输网络中的风险和成本。建立模型时充分考虑现实决策中诸多实际因素，首次在模型约束条件里加入了时间窗,考虑运输企业运输过程的时间成本，使模型更接近实际。结合一个具体算例进行分析，经过对危险品运输网络设计的一般措施进行比较，证明了双层规划模型用于危险品运输道路网络设计的有效性。在实际中获取数据并进行大规模的案例求解是以后研究的方向。

参考文献：

[1]LIST G F, MIRCHANDANI P B,TURNQUIST M A, et al. Modeling and analysis for hazardous materials transportation: Risk analysis, routing / scheduling and facility location[J] .Transportation Science, 1991,25(2):100-114.

[2]REN C, YUAN X，WANG J, et al. Study on emergency response rank mode of flammable and explosive hazardous materials road transportation[J].Procedia Engineering, 2012,45(2):830-835.

[3]MAHMOUDABADI A，SEYEDHOSSEINI S M .Developing a chaotic pattern of dynamic Hazmat routing problem[J]. Iatss Research,2014,37(2):110-118.

[4]MAHMOUDABADI A，SEYEDHOSSEINI S M. Solving hazmat routing problem in chaotic damage severitynetworkunderemergencyenvironment[J].Transport Policy,2014(36):34-45.

[5]于建平,杜纲.一类双层规划问题的遗传算法求解[J].重庆理工大学学报(自然科学),2013,28(4)：93-98.

[6]李昌兵,杜茂康，付德强.基于层次粒子群算法的非线性双层规划问题求解策略[J].系统工程理论与实践,2013,33(9)：2292-2298.

[7]KARA B Y, VERTER V. Designing a road network for hazardous materials transportation [J]. Transportation Science, 2004,38(2):188-196.

[8]ERHAN E, GZARA F. Solving the hazmat transport network design problem [J] . Computer s & Operations Research, 2008,35(7):2234-2247.

[9]储庆中,刘玉兵,吴国君.基于遗传算法求解的道路危险品运输线路优化双层规划模型[J].交通信息与安全,2011,29(2):95-99.

[10]蒋洋.基于结构和随机特性的交通网络设计问题研究[D].北京:北京交通大学,2011.

[11]张丽娜.道路危险品运输网络设计模型与算法研究[D].兰州：兰州交通大学,2013.