基于分离迭代和耦合时变的列车—轨道—桥梁耦合系统高效动力分析混合算法

朱志辉, 龚　威，张　磊，余志武，蔡成标

(1.中南大学 土木工程学院，湖南 长沙　410075；2.中南大学 高速铁路建造技术国家工程实验室，湖南 长沙　410075；3.西南交通大学 牵引动力国家重点实验室，四川 成都　610031)

自我国第一条高速铁路建成通车以来，目前中国高速铁路总里程已超过2万km，居世界第一。与普通铁路相比，评估高速铁路桥梁动力响应和列车行车安全性与乘坐舒适性指标必不可少[1]。随着车—桥耦合动力学的发展，多位学者指出，为准确评估上述指标，需要在车—桥耦合动力学模型中考虑轨道结构的柔性变形及参振作用[2]。当考虑轨道结构以后，由于轮轨间较大的接触刚度，导致车桥耦合动力分析的稳定性和收敛性问题变得更为复杂[3]；同时，对于大跨度桥梁而言，大量增加的轨道结构自由度将使耦合系统质量、刚度和阻尼矩阵规模呈几何倍数增加，导致动力分析计算量大幅增加[4]。因此，需要针对列车—轨道—桥梁耦合系统提出一种高效的计算方法。

很多学者针对车—桥耦合系统动力分析计算效率问题开展了研究工作，主要包括2个方面：模型简化和数值算法优化。Lou[5]建立了不等长的钢轨桥梁耦合单元，以减少桥梁结构自由度，并讨论了钢轨单元长度对钢轨与桥梁动力响应的影响。Yang[6]等假设轮对与钢轨始终密贴，同时将轮对的自由度压缩至钢轨。振型叠加法也常被用于减小桥梁结构自由度数目[7-8]，但很难选取合适的振型数量，以同时体现轨道结构的高频振动和桥梁结构的低频振动响应[9]。张楠等[10]提出了一种全过程迭代法，将列车和桥梁子系统间每一时间步内的迭代转换到了整个动力分析过程的迭代。Neves[11]等采用了优化的块式因式分解算法，提高了车桥耦合动力分析的效率。

以上研究在一定程度上提升了车—桥耦合系统动力响应的计算效率和稳定性，所采用的车—桥耦合系统动力方程求解方法主要分为2类：分离迭代法(Separation and Iteration Method, SIM)和耦合时变法(Coupled and Time-Dependent Method, CTM)[12]。其中SIM将车辆和桥梁视作2个独立的子系统，2个子系统间通过力的平衡与位移协调条件相互耦合，在每一时间步内需进行迭代求解。整个计算过程中，车辆子系统和桥梁子系统的质量、刚度和阻尼矩阵保持不变。该方法的主要缺点在于耦合系统动力计算稳定性受轮轨接触点处迭代收敛平衡条件控制，通常需要较小的时间积分步长(Δt≤10-4s)，以确保轮轨接触迭代计算收敛[2]。CTM直接建立车辆和桥梁耦合系统整体时变动力方程，在每一时间步内直接对动力方程进行求解[13-15]，避免了每一时间步内的轮轨力收敛迭代计算。但CTM需要在每一时间步根据车辆位置对耦合系统整体矩阵进行更新，尤其当车辆模型较为复杂或存在大量轮轨接触点时，会增大车—桥耦合模型动力系数矩阵的带宽，进而增加每一时间步的求解时间[16-17]。

为进一步提高列车—轨道—桥梁相互作用问题的计算效率，本文基于SIM和CTM，提出列车—轨道—桥梁耦合系统高效动力分析混合算法(Hybrid Solution Algorithm, HSA)。

1　列车、轨道、桥梁子系统模型及其动力方程

1.1　列车子系统

一列车由Nv节车辆组成，每节车辆仅考虑在竖向平面内的10个自由度，第j节车的10个自由度为车体沉浮zcj、车体点头θcj、转向架沉浮zb1j和zb2j、转向架点头θb1j和θb2j以及轮对的沉浮zw(4j-3)—zw4j(所有轮对按照行车方向从前到后按1—4Nv统一编号)。根据多刚体假定和线性悬挂系统假定，每节车的参数可以简化为：一系悬挂刚度kp和阻尼cp；二系悬挂刚度ks和阻尼cs；车体的质量mc和点头转动惯量Jc；构架的质量mb和点头转动惯量Jb；轮对的质量mw。轮轨之间采用Hertzian接触关系模拟。

根据D’Alembert原理，可建立基于平衡位置的列车子系统动力方程

(1)

列车子系统质量矩阵Mvv为

(2)

其中，

Mvj=diag(mcJcmbJbmbJbmw

mwmwmw)

式中：Mvj为第j节车的质量矩阵。

列车子系统刚度矩阵Kvv为

(3)

其中，

式中：Kvj为第j节车的刚度矩阵；Lc为车体定距之半；Lb为构架定距之半。

列车子系统阻尼矩阵可表示为

(4)

式中：Cvj为第j节车的阻尼矩阵，Cvj的形式与刚度矩阵Kvj相同，只需将Kvj的一系悬挂刚度kp与二系悬挂刚度ks替换成一系悬挂阻尼cp与二系悬挂阻尼cs即可。

列车子系统位移向量为

(5)

其中，

Xvj=(zcjθcjzb1jθb1jzb2jθcj

zw(4j-3)zw(4j-2)zw(4j-1)zw4j)

式中：Xvj为第j节车的位移向量。

1.2　轨道子系统

在车—桥耦合振动分析中，轨道结构的弹性变形作用既可以起到过滤轮轨高频振动的目的，还对轮轨力有显著影响[18]。以往的研究发现，模态叠加法虽然可以提高结构动力响应的计算效率，但是很难准确体现钢轨的局部高频振动特性[9]。因此，本文将采用直接刚度法建立轨道子系统模型。

轨道子系统动力方程为

(6)

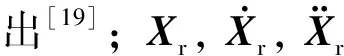
1.3　桥梁子系统

通过有限元方法建立精细化桥梁模型，采用直接刚度法建立桥梁子系统动力方程为

(7)

2　列车—轨道—桥梁耦合系统高效动力分析混合算法

HSA将列车—轨道—桥梁耦合系统分解为列车—轨道耦合时变子系统和桥梁子系统2部分，并通过轨道和桥梁在连接节点处的相互作用力将2个子系统耦合起来，实现列车—轨道—桥梁耦合系统的动力仿真分析，如图1所示。图中Frb为桥梁对钢轨的作用力向量，Fbr为钢轨对桥梁的作用力向量，v为列车车速。

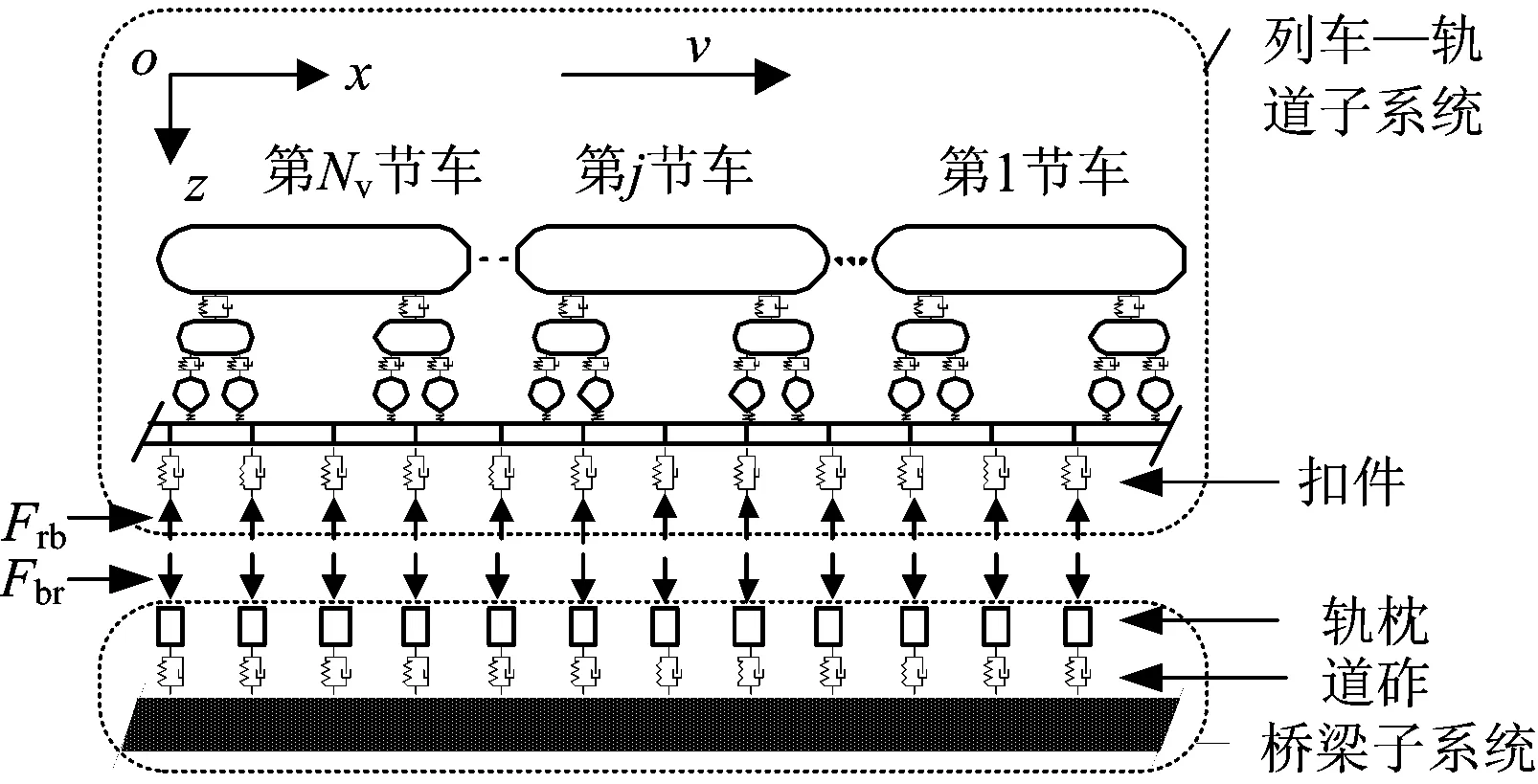
图1　列车—轨道—桥梁耦合系统示意图

由于HSA在计算过程中仅需更新列车—轨道时变子系统的动力系数矩阵，而式(7)所示的桥梁子系统动力系数矩阵具有时不变特征，因此，本节主要介绍列车—轨道时变子系统动力方程和HSA求解策略。

2.1　列车—轨道耦合时变子系统动力方程

列车子系统与轨道子系统通过轮轨接触关系耦合为列车—轨道子系统。根据已有的列车子系统动力方程与轨道子系统动力方程，利用“对号入座法则”[20]将轮轨接触关系直接写入列车与轨道的刚度矩阵及其耦合项中，即可得到列车—轨道子系统的动力方程

(8)

其中，

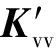
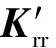
Fv=Fvg+Fvr

Fr=Frv+Frb

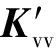
在列车—轨道子系统中，轮轨之间采用Hertzian接触模型[21]，由于Hertzian接触模型仅包含刚度项，因此公式(8)中仅刚度矩阵及荷载向量中存在耦合项。由轮轨接触引起的车辆刚度附加矩阵Kvh为

(9)

其中，

Kvhj=diag(0000002kh2kh

2kh2kh)

式中：Kvhj为轮轨接触对第j辆车的影响刚度矩阵；kh为赫兹弹簧刚度。

由轮轨接触引起的刚度附加矩阵Krr2为

(10)

式中：Nij为(1×Nr)维的向量，表示第i个轮对所在的第j个钢轨单元的三次Hermit插值形函数[17]；Nr为钢轨自由度数目。

列车运行过程中，列车与钢轨的刚度矩阵耦合项Kvr为

(11)

其中，

在列车—轨道子系统中，轮轨间的相互作用力为内力，故列车荷载项仅包含列车自重及轨道不平顺激励为

(12)

其中，

Fvgj=(mcg0mbg0mbg0mwg

mwgmwgmwg)

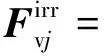
外荷载中车辆对轨道作用仅包含轨道不平顺激励：

(13)

2.2　列车—轨道子系统与桥梁子系统耦合作用

列车—轨道子系统与桥梁子系统间通过梁轨间相互作用力实现耦合，桥梁对钢轨的作用力Frb为

(14)

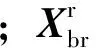
钢轨对桥梁的作用力Fbr为

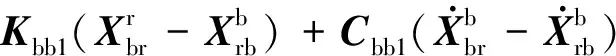
(15)

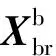
2.3　HSA计算流程

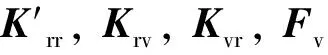
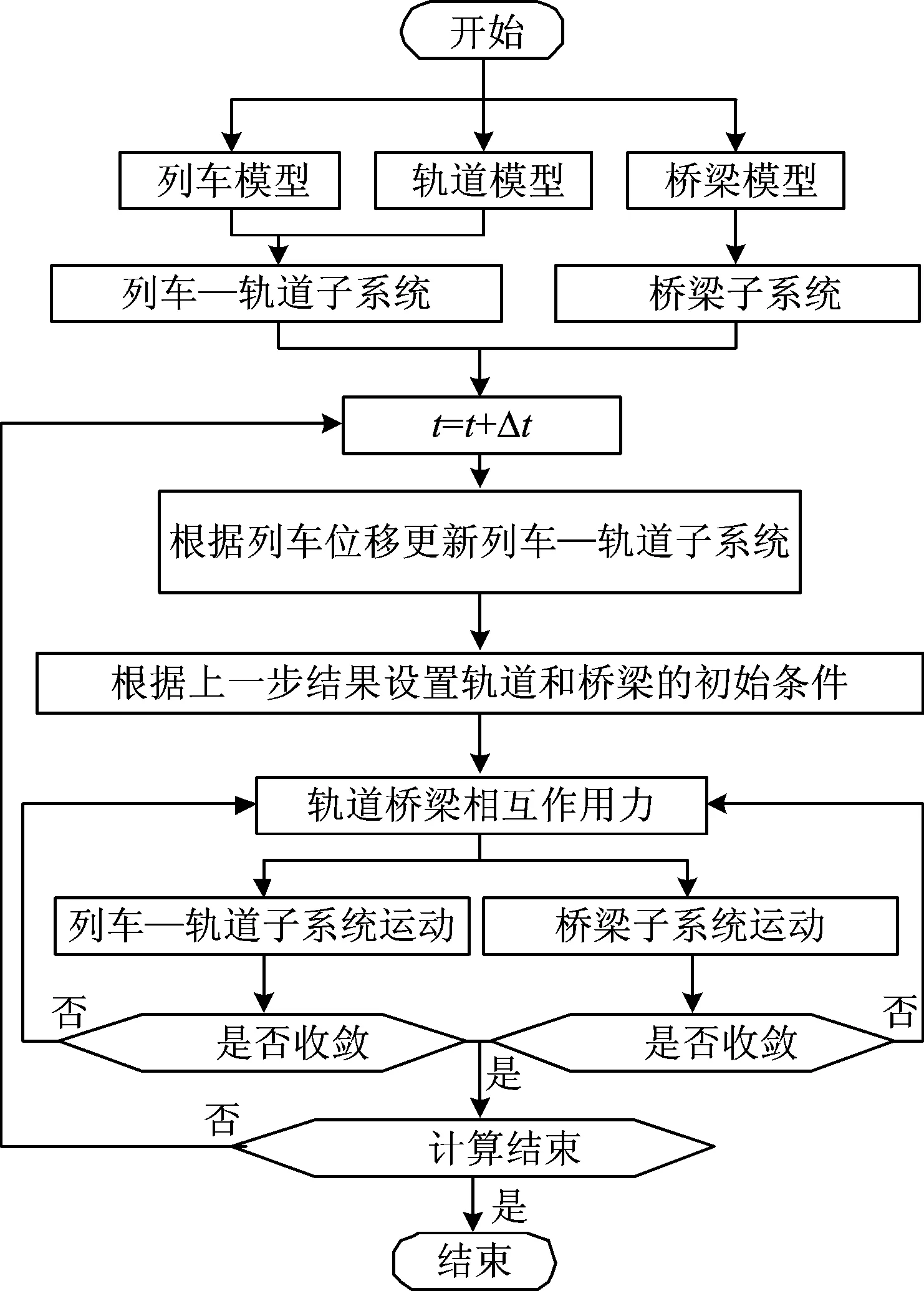
图2　HSA计算流程

与传统基于CTM的整体列车—轨道—桥梁耦合时变动力学模型相比，HSA将钢轨与桥梁解耦，大大降低了列车—轨道时变子系统和桥梁子系统动力系数矩阵的带宽；同时在计算过程中仅需更新列车—轨道时变子系统的动力系数矩阵，桥梁子系统的动力系数矩阵具有时不变特征。相较于CTM，HSA具有更高的计算效率。HSA通过钢轨与桥梁间作用力的平衡迭代实现列车—轨道时变子系统和桥梁子系统耦合，相对于以往基于轮轨力平衡迭代的SIM而言，由于钢轨与桥梁间的接触刚度远远小于轮轨间的接触刚度，因此HSA的迭代稳定性更优。

3　方法验证

为验证本文HSA的正确性，以图3所示的朔黄重载铁路32 m简支梁桥为例，分别采用HSA与CTM计算车辆过桥的动力响应，并与现场实测数据对比，验证HSA的正确性。

图3　朔黄重载铁路32 m简支梁现场图

3.1　工程概况

朔黄重载铁路32 m简支梁桥由4根超低高度的预应力T型梁组成，混凝土强度等级为C60。钢轨为75 kg·m-1标准轨，轨枕为Ⅲ型混凝土轨枕，道床厚度为22 cm。轨道及桥梁详细参数见表1。

试验列车编组为“2节提速机车+116节C80重载列车”，详细参数见表2。列车编组总长度为1 424.6 m。列车以71.57 km·h-1的速度单线行驶过桥。

3.2　轨道、桥梁有限元模型

采用ANSYS建立轨道、桥梁有限元模型。其中，钢轨、轨枕、主梁均采用梁单元进行模拟，单元长度均为0.6 m。轨枕与桥面的连接以及钢轨与轨枕的连接通过弹簧—阻尼器单元模拟。为模拟列车上桥时的初始振动状态，在桥梁两侧各添加32 m的轨道延长段。由于只考虑列车经过重载线的情况，且重载线和轻载线相互分离，所以忽略轻载线部分。轨道不平顺采用美国FRA5级轨道谱。根据以上的建模原则，建立了如图4所示的轨道、桥梁整体三维有限元模型。

表1　轨道及桥梁参数

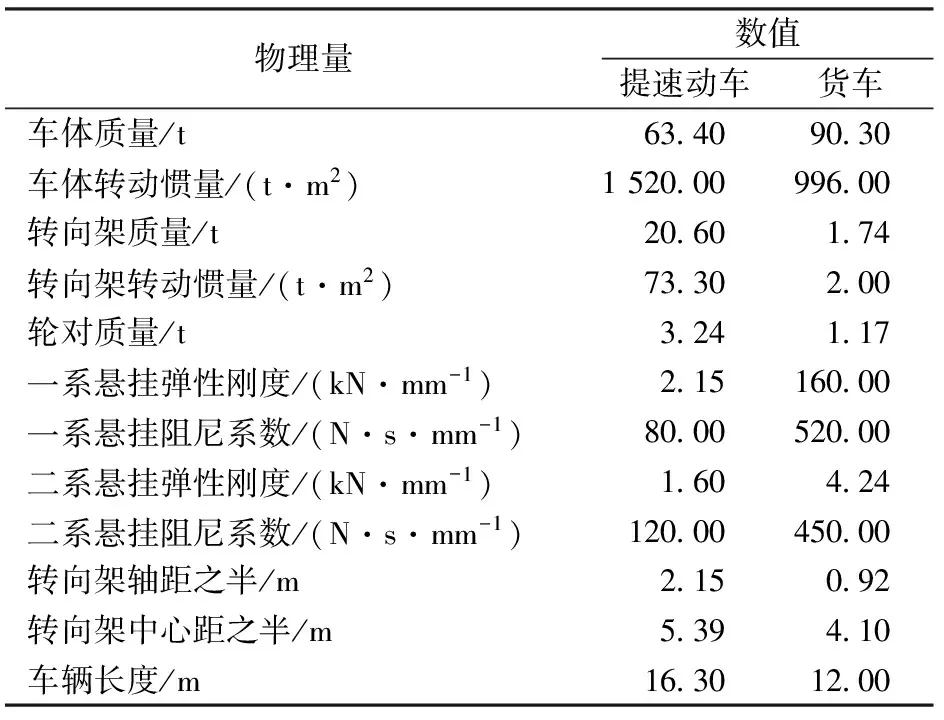
表2　提速机车及货运列车参数表

3.3　结果分析

图5中给出了HSA与CTM计算所得桥梁跨中竖向位移结果与实测结果。从图5中可以看出，HSA与CTM计算的桥梁跨中位移响应时程曲线几乎完全重合，二者误差最大值仅为0.03%；同时，HSA计算结果与试验数据误差为1.79%，表明采用HSA分析车—桥耦合动力响应问题，可以得到满意的精度。

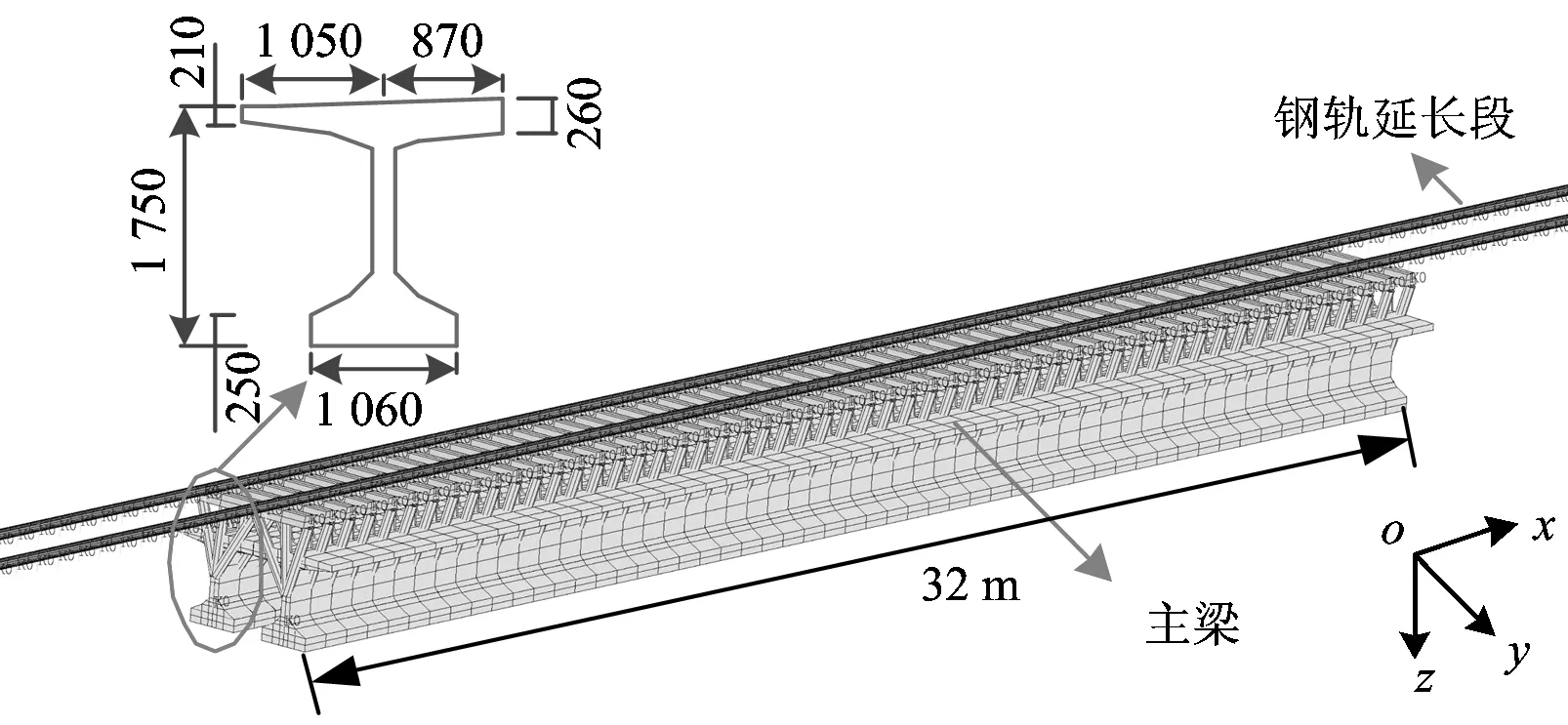
图4　桥梁有限元模型(单位：mm)

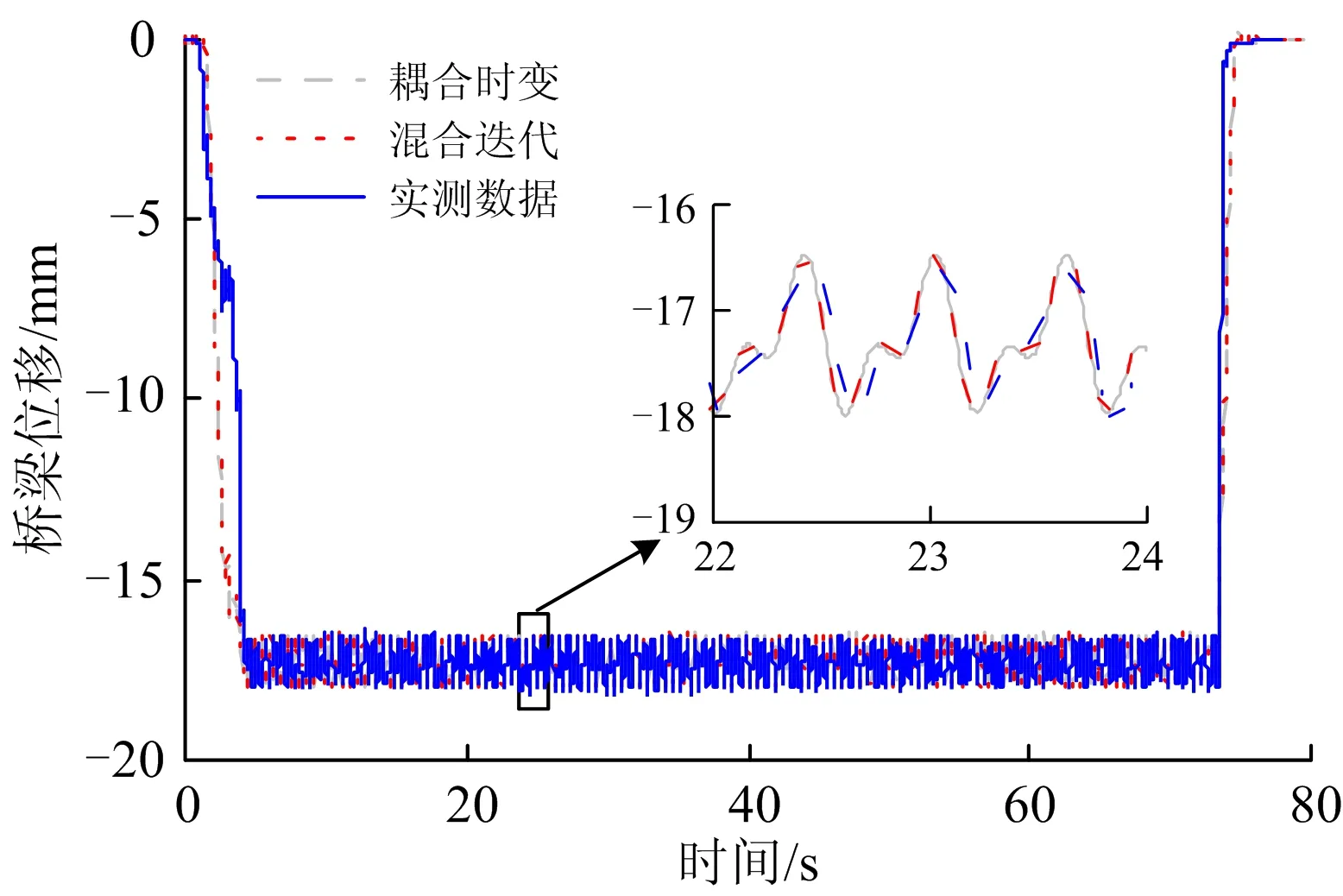
图5　桥梁跨中竖向位移时程

4　蒙华铁路龙门黄河大桥动力分析

4.1　工程概况

为进一步对比HSA和CTM的计算效率，本节以蒙华铁路龙门黄河大桥为例进行对比分析。该桥为中承式钢管混凝土拱桥，钢管混凝土拱跨度202 m，矢跨比1/4，其跨度布置如图6所示。铁路等级为国铁Ⅰ级，重载铁路标准，采用双正线，线间距为4.0 m，设计行车速度120 km·h-1。桥梁所有材料均假设为线弹性，钢材弹性模量取210 GPa，混凝土强度等级为C50；墩身、桥面板采用C40混凝土；吊杆采用整束挤压式钢绞线拉索体系，钢绞线抗拉强度为1 860 MPa。桥面二期恒载为134 kN·m-1(已扣除轨道结构二期恒载16 kN·m-1)，包括防水层、保护层、人行道、照明设施等。

图6　桥梁构造示意图 (单位：m)

4.2　轨道、桥梁模型

轨道、桥梁有限元模型如图7所示。其中，桥梁支座、轨枕与桥面的连接以及钢轨与轨枕的连接通过弹簧—阻尼器单元模拟。根据文献[23]和设计图纸资料，弹簧—阻尼器单元参数见表3。桥梁支座布置如图6所示，共设置16个支座，其中活动支座只设置y和z方向的约束，固定支座设置了x,y和z方向的约束，桥梁拱脚与桥墩墩底均固结。为模拟列车上桥前的初始振动状态，在桥梁两侧各添加30 m的轨道延长段。

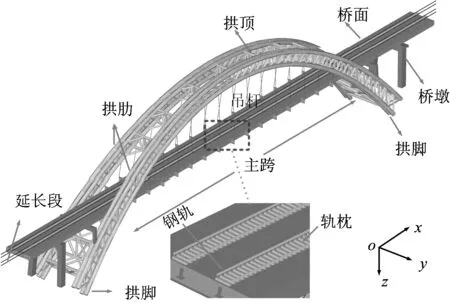
图7　拱桥有限元模型

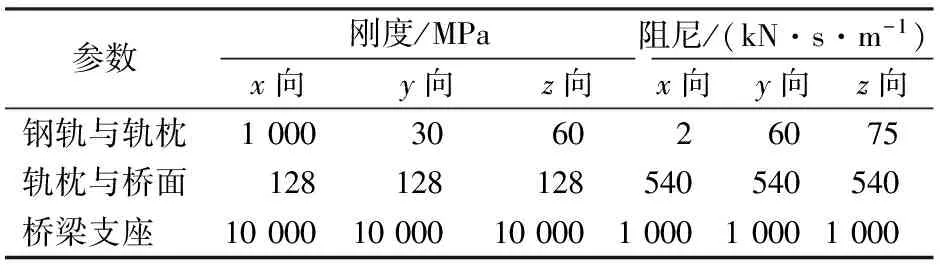
参数刚度/MPa阻尼/(kN·s·m-1)x向y向z向x向y向z向钢轨与轨枕1000306026075轨枕与桥面128128128540540540桥梁支座　100001000010000100010001000

4.3　结果分析

选取与桥长大致相等的列车编组开展耦合系统动力分析，使列车长度足以覆盖整座桥面。列车编组为2节提速机车+20节C80型货车的重载列车，列车编组总长度272.6 m。列车以120 km·h-1的设计速度单线行驶过桥，采用美国五级轨道不平顺谱，积分步长取1/1 000 s。

图8和图9别给出了HSA和CTM计算的列车和桥梁跨中位置的动力响应时程曲线。从图8和图9中可以看出，2种方法计算所得第一个轮对竖向轮轨力时程、第一节车车体竖向加速度时程、桥梁跨中竖向位移时程和竖向加速度时程结果吻合度较好，最大误差均在3%以内。

图10为跨中位置处钢轨竖向振动加速度时程。从图10可以看出：2种方法计算结果吻合程度稍差，最大误差为8.13%。需要指出的是，经过试算，SIM需采用小于或等于2×10-4s的时间积分步长才可以得到收敛结果，从而表明HSA较SIM具有更好的迭代稳定性。

HSA和CTM的计算耗时见表4。由表4可知，CTM计算耗时为369 min，HSA计算耗时为92 min，HSA较之CTM求解耗时缩短了75%，HSA可有效提升列车—轨道—桥梁耦合系统动力响应计算效率。

图8　车辆动力响应

图9　桥梁跨中动力响应

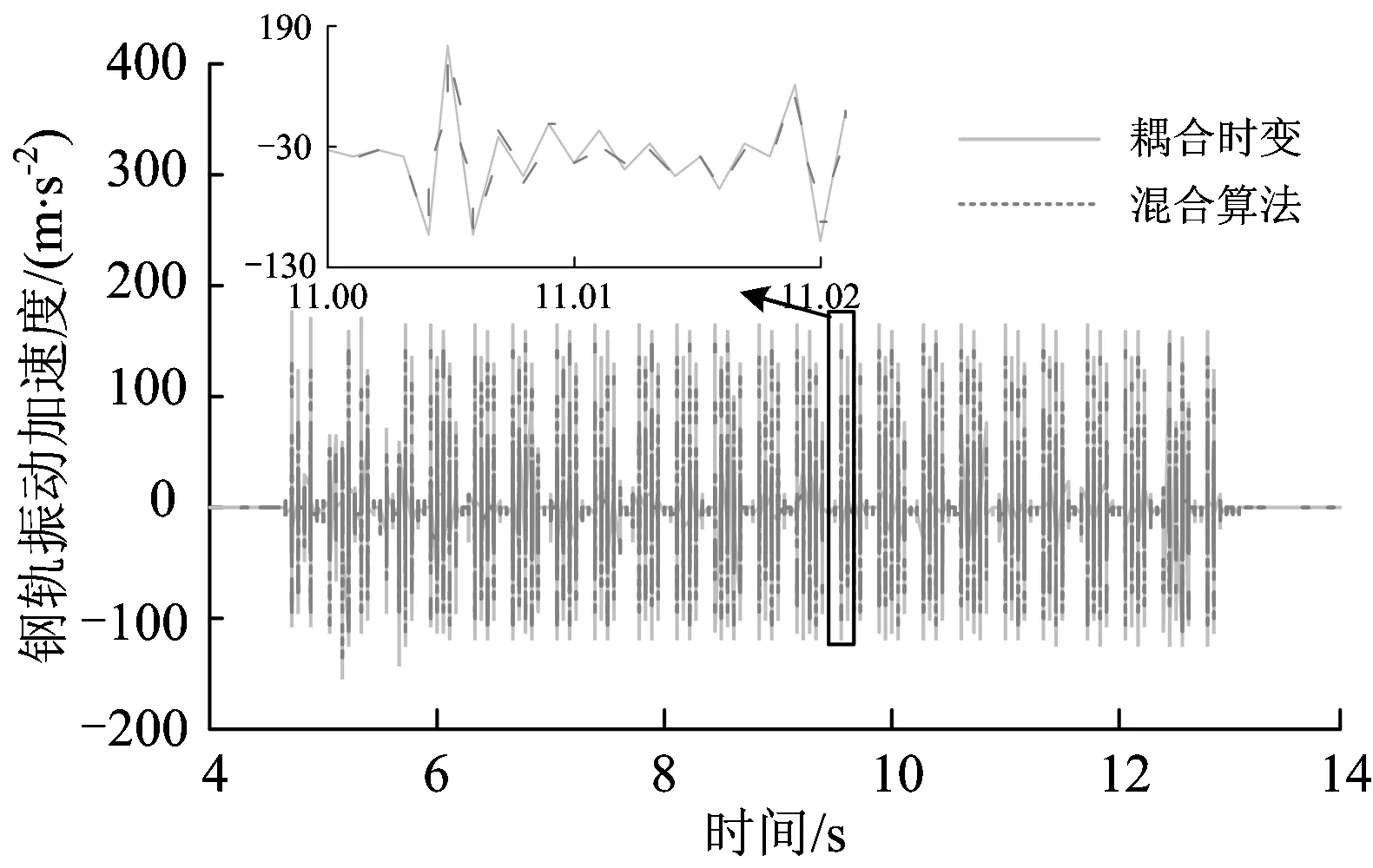
图10　跨中钢轨竖向振动加速度时程

表4　2种方法计算耗时对比

5　结　论

(1)HSA计算结果与耦合时变计算结果及现场实测数据吻合度极高，证明了HSA的准确性。

(2)HSA仅需将列车和轨道通过轮轨接触关系组成耦合时变子系统，从而简化了列车—轨道—桥梁耦合系统动力方程的理论推导过程，降低了建模难度；同时，列车—轨道子系统耦合时变动力方程不受下部桥梁结构矩阵的影响，因此HSA对于不同桥梁结构具有一定通用性。

(3)HSA在求解过程中，仅上部列车—轨道子系统的质量、刚度、阻尼矩阵是时变的，需要在每一时间步进行更新；下部桥梁子系统各项矩阵保持不变，不需要进行更新。

(4)与CTM相比，HSA每一步更新矩阵所需时间大大减少。以蒙华铁路龙门黄河大桥算例表明，HSA相较于传统的CTM，求解耗时降低了75%。

[1]DIMITRAKOPOULOS E G, ZENG Qing. A Three-Dimensional Dynamic Analysis Scheme for the Interaction between Trains and Curved Railway Bridges[J]. Computers & Structures, 2015, 149: 43-60.

[2]吴定俊, 李奇, 陈艾荣. 车桥耦合振动迭代求解数值稳定性问题[J]. 力学季刊, 2007, 28(3): 405-411.

(WU Dingjun, LI Qi, CHEN Airong. Numerical Stability of Iteration Scheme for Solution of Vehicle-Bridge Coupling Vibration [J]. Chinese Quarterly of Mechanics, 2007, 28(3): 405-411.in Chinese)

[3]杜宪亭, 夏禾, 张田. 车桥耦合振动迭代求解稳定性研究[J]. 振动与冲击, 2012, 31(22): 62-65.

(DU Xianting, XIA He, ZHANG Tian. Numerical Stability of Iterative Scheme in Solving Coupled Vibration of a Train-Bridge System [J]. Journal of Vibration and Shock, 2012, 31(22): 62-65. in Chinese)

[4]LI Yongle, SU Yang, XIA Feilong, et al. Vertical Dynamic Response of the Ballastless Track on Long-Span Plate-Truss Cable-Stayed Bridges [J]. Science China Technological Sciences, 2015, 58(2): 236-247.

[5]LOU Ping, YU Zhiwu, AU F T K. Rail-Bridge Coupling Element of Unequal Lengths for Analysing Train-Track-Bridge Interaction Systems [J]. Applied Mathematical Modelling, 2012, 36(4): 1395-1414.

[6]YANG Yeongbin, WU Yeanseng. A Versatile Element for Analyzing Vehicle-Bridge Interaction Response [J]. Engineering Structures, 2001, 23(5): 452-469.

[7]SALCHER P, ADAM C. Modeling of Dynamic Train-Bridge Interaction in High-Speed Railways [J]. Acta Mechanica, 2015, 226(8): 2473-2495.

[8]JIN Zhibin, PEI Shiling, LI Xiaozhen, et al. Vehicle-Induced Lateral Vibration of Railway Bridges: an Analytical-Solution Approach[J]. Journal of Bridge Engineering, 2015, 21(2)：04015038.

[9]ZHANG Nan, XIA He, GUO Weiwei, et al. A Vehicle-Bridge Linear Interaction Model and Its Validation[J]. International Journal of Structural Stability & Dynamics, 2012, 10(2): 335-361.

[10]ZHANG Nan, XIA He. Dynamic Analysis of Coupled Vehicle-Bridge System Based on Inter-System Iteration Method [J]. Computers & Structures, 2013, 115(1): 26-34.

[11]NEVES S G M, MONTENEGRO P A, AZEVEDO A F M, et al. A Direct Method for Analyzing the Nonlinear Vehicle-Structure Interaction [J]. Engineering Structures, 2014, 69(11): 83-89.

[12]CHEN Zhiwei, CHEN Bo. Recent Research and Applications of Numerical Simulation for Dynamic Response of Long-Span Bridges Subjected to Multiple Loads [J]. Scientific World Journal, 2014, 2014(2): 763810.

[13]WANG Wei, YAN Wangchen, DENG Lu, et al. Dynamic Analysis of a Cable-Stayed Concrete-Filled Steel Tube Arch Bridge under Vehicle Loading[J]. Journal of Bridge Engineering, 2015, 20(5): 1-20.

[14]DENG Lu, CAI C S. Development of Dynamic Impact Factor for Performance Evaluation of Existing Multi-Girder Concrete Bridges[J]. Engineering Structures, 2010, 32(1): 21-31.

[15]GUO W H, XU Y L. Fully Computerized Approach to Study Cable-Stayed Bridge-Vehicle Interaction[J]. Journal of Sound & Vibration, 2001, 248(4): 745-761.

[16]GU G. Resonance in Long-Span Railway Bridges Carrying TGV Trains[J]. Computers & Structures, 2015, 152: 185-199.

[17]LOU Ping. Finite Element Analysis for Train-Track-Bridge Interaction System[J]. Archive of Applied Mechanics, 2007, 77(10): 707-728.

[18]张攀, 周昌盛, 王平. 轨下垫板刚度的时变特性及其影响研究[J]. 铁道标准设计, 2015(9): 49-52.

(ZHANG Pan, ZHOU Changsheng, WANG Ping. Study on Time Variant Characteristics and Effects of Rail Pad Stiffness [J]. Railway Standard Design, 2015(9): 49-52. in Chinese)

[19]朱志辉, 龚威, 王力东, 等. 列车—轨道—桥梁耦合系统动力方程求解方法对计算精度和效率的影响[J]. 中国铁道科学, 2016, 37(5): 17-26.

(ZHU Zhihui, GONG Wei, WANG Lidong, et al. Influence of Solution Method for Dynamics Equation of Train-Track-Bridge Coupled System on Calculation Precision and Efficiency [J]. China Railway Science, 2016, 37(5): 17-26. in Chinese)

[20]曾庆元, 杨平. 形成矩阵的“对号入座”法则与桁梁空间分析的桁段有限元法[J]. 铁道学报, 1986,8(2): 50-61.

(ZENG Qingyuan, YANG Ping. The “Set-in-Right-Position” Rule for Forming Structural Matrices and the Finite Truss-Element Method for Space Analysis of Truss Bridges [J]. Journal of the China Railway Society, 1986, 8(2): 50-61. in Chinese)

[21]朱志辉, 王力东, 龚威, 等. 基于改进迭代模型的车桥耦合系统竖向随机振动研究[J]. 湖南大学学报:自然科学版, 2016, 43(11): 120-130.

(ZHU Zhihui, WANG Lidong, GONG Wei, et al. Study on Vertical Random Vibration of Train-Bridge Coupled System Based on Improved Iteration Model [J]. Journal of Hunan University:Natural Sciences, 2016, 43(11): 120-130. in Chinese)

[22]NGUYEN D V, KIM K D, WARNITCHAI P. Simulation Procedure for Vehicle-Substructure Dynamic Interactions and Wheel Movements Using Linearized Wheel-Rail Interfaces[J]. Finite Elements in Analysis and Design, 2009, 45(5): 341-356.

[23]刘玮, 曲村. 高速铁路桥上有砟轨道轨枕选型方案研究[J]. 高速铁路技术, 2011, 2(3): 38-42.

(LIU Wei, QU Cun. Study on Selection of Sleepers for Ballasted Track on Bridges of High-Speed Railway [J]. High Speed Railway Technology, 2011, 2(3): 38-42. in Chinese)