求解并行测试任务调度问题的ACIA
李文海,管 晗
(海军航空大学 a.科研部;b.研究生管理大队, 山东 烟台 264001)
并行测试与传统串行测试相比,提高了资源利用率,节约了测试时间。但是其任务调度是个复杂、难以优化的NP难题[1]。
国内外众多专家学者都研究了并行测试的任务调度问题。文献[1]对并行测试技术进行了综述;文献[2]提出基于Petri网的并行测试系统建模过程;文献[3-5]分别运用TaskScheduler-T算法、改进粒子群算法(IPSO)以及混合遗传算法,建立了并行测试模型,在任务调度问题上取得了一定的成果。
为进一步提高系统测试资源利用率和测试效率,本文提出了一种自适应混沌免疫算法(Adaptive Chaos Immune Algorithm,ACIA),即利用混沌优化理论的遍历性、随机性等优势,将混沌优化理论引入人工免疫算法,形成改进的新算法。并将改进的算法应用于求解并行测试任务调度的问题中。
1 混沌优化理论
混沌是指在确定系统中出现的一种貌似无规则,类似随机的现象,是存在于非线性系统中的一种较为普遍的现象。混沌并不是一片混乱,而是有着精致内在结构的一类现象。混沌是非线性动力学系统在一定条件下所表现的一种运动形式,是系统处于非平衡过程中所呈现的随机行为[6]。混沌的主要特征有:非线性、对初始条件敏感的依赖性、长期行为的不可预测性、不可分解性、稳定性和不稳定性、具有规律性成分、遍历性、分形性[7]。
设连续自映射f:I→I⊂R,I是R中的一个子区间。如果存在不可数集合S⊂I满足:
1)S不包含周期点;
2) 任给X1,X2∈SX1≠X2,有

混沌映射是混沌优化理论中重要的一部分,通过混沌映射公式可以产生一系列处于混沌状态的值和值空间。一般采用Logistic映射,其计算公式为
xn+1=μxn1-xn
(1)
其中,xn∈0,1,μ∈0,4为混沌控制变量。根据文献[9],当μ=4时,xn的取值遍布0,1,达到最佳混沌效果,因此使用Logistic映射时,一般取μ=4。
2 自适应混沌免疫算法
免疫克隆选择算法(Immune Clonal Selection Algorithm,ICSA)是人工免疫算法的核心算法之一,是模拟自然免疫系统功能的一种新的智能方法,具有学习记忆功能[10-11],该算法具有全局搜索能力强、收敛速度快和鲁棒性强等优点。其算法的基本流程如图1所示。
由于免疫算法在搜索过程中易出现早熟、易陷入局部最优和寻优结果不稳定的特点,本研究结合混沌优化的随机性,遍历性和对初始条件的敏感性等优点,提出一种自适应混沌免疫算法(ACIA)。
2.1 算法步骤
自适应混沌免疫算法的步骤如下:
步骤1混沌初始化种群,生成抗体数量为N的初始抗体群体P;
步骤2根据亲和度函数,计算各抗体的亲和度,挑选出亲和度高的前N1个最优抗体,构成克隆体种群B;
步骤3对克隆体种群B进行自适应克隆(复制)操作,得到新的抗体种群C;
步骤4对克隆体种群C进行基于混沌扰动的变异操作,得到抗体种群D,然后加入抗体种群;
步骤5对抗体种群D进行浓度调节操作,得到抗体种群E;
步骤6将抗体种群E中亲和度最高的抗体加入记忆群体集合中;用记忆群体集合中的高亲和度个体代替抗体集合中低亲和度的抗体,更新抗体群体集合;
步骤7返回步骤2进行迭代,直到满足停止条件,迭代结束,输出结果。

图1免疫克隆选择算法流程
2.2 ACIA求解并行测试任务调度问题
在并行测试任务调度问题中,调度的目标函数即测试总时间,对应于算法中的抗原;调度的候选序列对应于抗体;候选序列相对于目标函数的质量对应于抗原和抗体的亲和度。
算法的改进主要在混沌初始化、基于混沌扰动的变异和浓度调节操作。改进后的算法具体步骤如下:
1) 混沌初始化
(2)
其中,randperm*为随机排列函数。
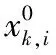
(3)
d) 将混沌序列转化为免疫算法初始化基因。利用式(3)做逆变换为
(4)
得到自适应混沌免疫算法的初始种群
(5)
2) 目标函数和亲和度
目标函数MakeP为测试时间,即变迁序列的时延总和。测试的最优序列即为测试时间最短的序列,得到任务调度最优方案的算法的基本思想如下:
a) 每个序列从第一个元素开始,找出能与之连续并行的选项,以括号标记,遇到不能并行的停止;然后以括号截止前一个元素开始,继续判断与后面元素是否并行,直到序列结束。
b) 若没有并行关系,则能确定前一个元素时间。
c) 若存在并行关系,则比较括号开始前一个元素时间与括号中所有元素时间和的大小。
① 括号开始前一个元素时间大:前一个元素时间不变,括号中所有元素时间置为0;
② 括号中所有元素时间和大:前一个元素时间不变,从括号开始到括号结束元素前一位元素时间置为0;括号结束元素时间为括号开始前一个元素时间与括号中所有元素时间和的差值的绝对值。
亲和度反映了变迁序列的质量,由目标函数的某种变换表示。假设某测试系统串行测试的总时间为T,所以构造第i个测试序列的亲和度函数定义为
Aff1,i=T-MakeP1,i
(6)
3) 自适应克隆操作
将抗体种群P中的抗体根据亲和度大小进行降序排序,得到亲和度较高的前N1个抗体,构成克隆体种群B;克隆体数量N1=Pa×N,其中Pa为克隆选择概率,N为初始抗体数;再对克隆体种群B进行克隆,克隆数目MM定义为
(7)
其中,Mn(i)为每个抗体需要克隆的抗体数,定义为
(8)
其中:M为细胞克隆数;Mn(i)可根据该抗体的亲和度自适应调整;Int*为上取整函数。克隆过后,得到新的抗体种群C。
4) 基于混沌扰动的变异操作
变异操作采用位交换方法。首先采用混沌映射公式(1)随机生成两个混沌变量;然后通过变异率决定是否变异,如果变异概率小于变异阈值Pz,则将两个变量映射到抗体编码的具体位置上,然后对这两个编码进行交换,则实现了抗体的变异。变异结束后抗体种群D取代种群C,进入下一步循环。
5) 浓度调节操作
利用浓度调节机制,实现抗体间促进和抑制的相互关系。第i个抗体的选择概率为
Pci=αPAffi+1-αPNongi
(9)
其中:α为常数调节因子;PAffi为亲和度概率;PNongi为浓度抑制概率
(10)
(11)
其中:β为常数调节因子;Nong(1,i)为第i个抗体浓度
(12)
其中:Ayy1,i为第i个抗体与本次迭代种群最优个体的相似度;Py为浓度抑制半径。
(13)
其中,Pij为第i个符号出现在第j个基因座上的概率,定义为
(14)
根据式(9)可知,第i个抗体的选择概率与该抗体的亲和度成正比,与该抗体的浓度成反比。通过该式的浓度调节,既能保留亲和度高的抗体,又能抑制高亲和度、高浓度的抗体,保障了抗体种群的多样性。
6) 停止条件
设置算法的停止条件为迭代次数达到阈值或者测试序列时间多次迭代保持不变。
3 实验仿真
以两台某型雷达接收机的并行测试系统为例。雷达测试系统的资源集R={r1,r2,r3,r4,r5,r6,r7},其中r1为扫频信号源,r2为标量网络分析仪,r3为频谱仪,r4为示波器,r5为程控直流电源,r6为矢量网络分析仪,r7为功率计。雷达接收机的各个待测参数就是各个测试任务,表1给出了雷达测试系统的测试任务资源集。待测参数即各项测试任务,测试时间即完成某待测参数测试所需的时间,单位为秒。
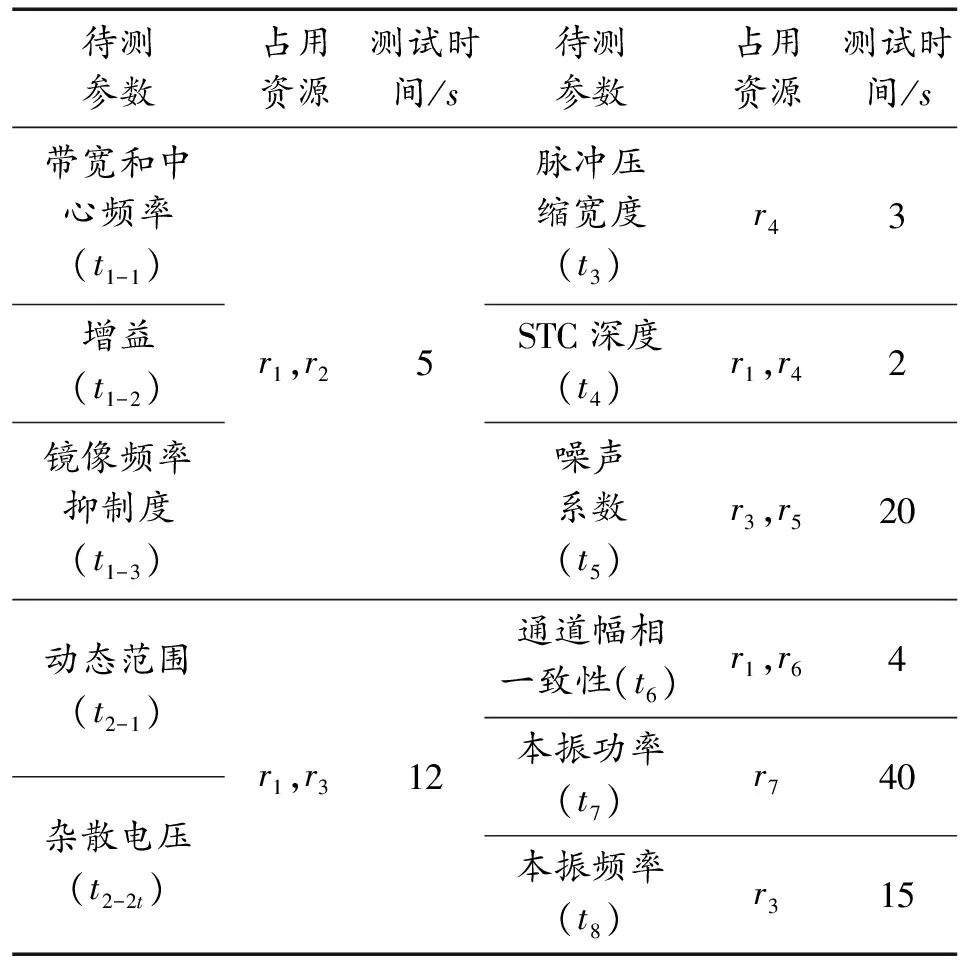
表1 雷达接收机测试任务资源集
表1中任务t1-1,t1-2,t1-3都占用资源r1,r2,可合并为一个任务,记作t1。同理,可将任务t2-1,t2-2合并为一个任务,记作t2。由此可得,雷达接收机测试任务与测试资源的关系为:t1〈r1,r2〉,t2〈r1,r3〉,t3〈r4〉,t4〈r1,r4〉,t5〈r3,r5〉,t6〈r1,r6〉,t7〈r7〉,t8〈r3〉。
以完成两台雷达接收机所有测试任务所需测试时间最短的测试序列为最优的任务调度目标,建立并行测试模型。算法参数设置为初始抗体数N=100,迭代阈值IerativeTime=100,串行测试总时间T=202 s,克隆选择概率Pa=0.7,细胞克隆数M=200,变异概率Pz=0.6,浓度抑制半径Py=0.7。假设各个测试任务是相互独立的,没有顺序约束。

将自适应混沌免疫算法与文献[3]中的TaskScheduler-T算法和未改进的人工免疫算法(ICSA)进行比较,得到比较结果如表2与图3所示。
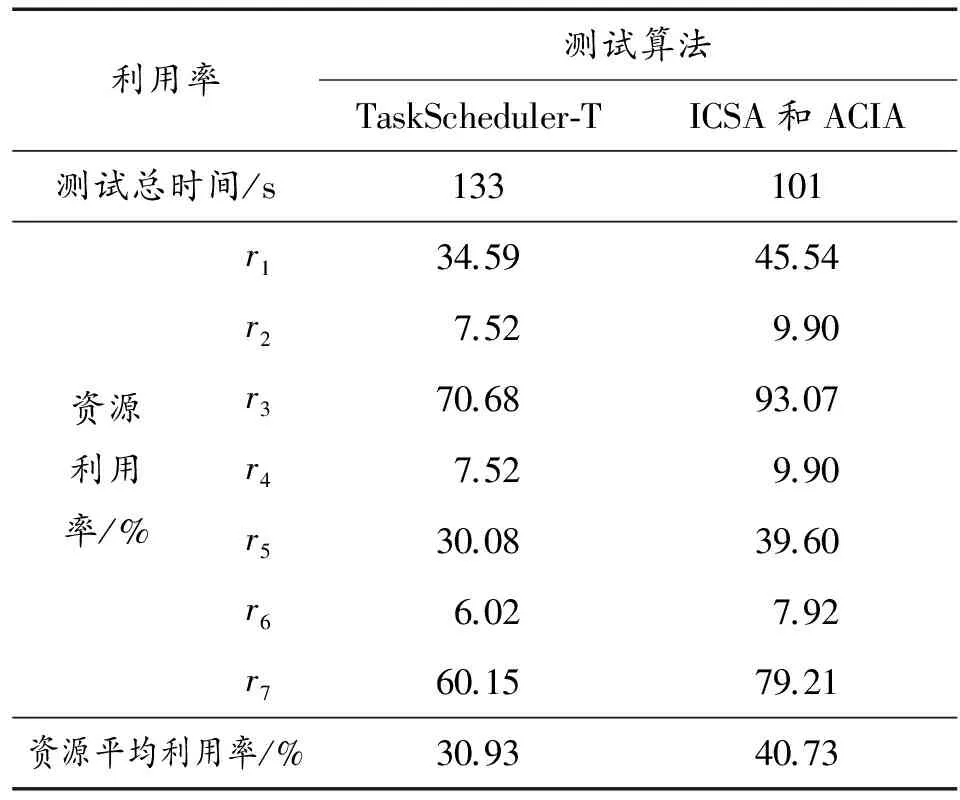
表2 各算法资源利用率与测试总时间比较
从表2可以看出,与TaskScheduler-T算法相比,ICSA和ACIA完成测试的总时间减少了32 s,即测试效率提高了24.06%,测试资源的平均利用率提高了9.80%。
由MATLAB仿真得到ICSA和ACIA测试总时间与迭代次数的关系对比如图3所示。
从图3可以看出,由于ACIA在初始化阶段加入了混沌优化,与ICSA相比,迭代初期搜索范围较大,得到的测试序列更具有遍历性、随机性;两种算法在迭代初期的收敛性都不错,但随着迭代次数的增加,ICSA搜索能力变弱,且易陷入局部最优。而ACIA由于添加了混沌扰动,能够不断收敛,提高了其种群多样性;最终,ACIA经过14次迭代找到测试时间最短的最优序列,而ICSA经过21次迭代才找到最优序列。因此,ACIA比ICSA的程序执行时间大大减少,测试效率大大提高。
综上所述,自适应混沌免疫算法的执行时间更短,效率更高,性能更优。
4 结论
本文基于人工免疫算法,结合混沌优化理论能够克服免疫算法易早熟、易陷入局部最优的缺陷,并针对并行测试任务调度问题进行优化。在人工免疫算法初始化阶段进行混沌优化;克隆操作中运用与亲和度相关的自适应克隆算子;变异操作中添加混沌扰动;并添加浓度调节操作。仿真实验表明,该算法能够较快地得到任务调度最优序列,较好地解决并行测试任务调度复杂、难以优化的问题。
与TaskScheduler-T算法和ICSA算法相比,该算法还具有迭代次数少、程序执行时间短、测试资源利用率高和测试性能优等优点。综上所述,对于解决并行测试任务调度问题,自适应混沌免疫算法表现出了良好的寻优性能。这为今后研究并行测试任务之间具有顺序约束的课题,提供了良好的理论支撑。
参考文献:
[1]肖明清,朱小平,夏锐.并行测试技术综述[J].空军工程大学学报:自然科学版,2005,6(3):22-25.
[2]卓家靖,孟晨.基于Petri网的并行测试系统任务过程建模[J].计算机工程与设计,2010(2):309-312.
[3]姚静波,辛朝军,蔡远文.一种基于多测试资源的并行测试任务调度算法[J].兵工自动化,2014(10):22-24,36.
[4]李文海,王怡苹,尚永爽,等.基于有色Petri网和IPSO的并行测试系统任务调度研究[J].计算机测量与控制,2011,19(10):2390-2393,2396.
[5]秦勇,梁旭.基于混合遗传算法的并行测试任务调度研究[J].国外电子测量技术,2016,35(9):72-75.
[6]唐娜,张公让,李磊.自适应混沌搜索的双粒子群优化算法[J].计算机工程与设计,2016(9):2421-2428.
[7]吕晓明,黄考利,连光耀.基于混沌遗传算法的测试选择优化问题研究[J].导弹与制导学报,2009,29(3):265-268.
[8]赵欣.不同一维混沌映射的优化性能比较[J].计算机应用研究,2012(3):913-915.
[9]赵岩松.基于自适应混沌的多核任务调度算法研究[D].西安:西安电子科技大学,2014.
[10] 苗国义,穆瑞辉,许加月.基于改进人工免疫算法的模糊Petri网参数优化[J].微电子学与计算机,2013,30(9):102-105.
[11] 杨斌,陆余良,杨国正,等.人工免疫理论在异常检测中的应用进展[J].计算机应用研究,2016,33(4):961-966.

