流体矢量推进特性分析和控制
屈高敏,李继广
(1.西安航空学院, 西安 710077; 2.南京航空航天大学, 南京 210094)
推力矢量装置可显著提高飞行器的机动性和可操纵性,在有人机和无人机上都已尝试使用并得到了有效验证[1-4]。已经投入使用的矢量装置为机械式矢量喷管,该装置由于需要作动系统驱动从而提高了质量和系统的复杂性。流体矢量喷管相比于机械式矢量喷管其结构简单,质量轻,成本低,可靠性高等优点[5-11]。相比于机械矢量喷管,流体矢量喷管质量减少24%~80%,发动机推质比提高7%~12%,成本和维护费用降低37%~53%。同时由于该喷管几何形状固定,消除了运动部件和缝隙,可以减小雷达散射截面,提高飞机的隐身性能[12-15]。
飞翼无人机由于取消了垂尾以及力臂短带来的舵面效率低,使得该布局的无人机操纵能力不足。在大迎角条件下,由于机身的遮挡,舵面处于机身气流分离部位,控制效率进一步下降,所以大迎角条件下的飞翼无人机控制是控制器设计的一大难点。解决该问题的途径一般包括采用更先进的控制理论设计控制器和更有效的控制舵面。流体矢量技术可以作为新型控制舵面。为飞翼无人机控制提供了新的思路,是解决该问题的有效途径之一。
由于流体推力矢量喷管的诸多优点,对该技术的研究已是航空技术领域的研究热点之一。文献[15]中根据激波矢量控制喷管矢量角随落压比的增大而下降的事实,提出了多缝辅助注气方法。文献[16]中应用数值模拟方法研究了喷口位置对激波控制的二维收-扩(2DCD)喷管矢量偏转的影响。根据文献[17]、文献[18]中设计了一种二元流体矢量喷管,采用一种无源被动二次流注入的流动控制手段,通过限制被动式二次流流通面积的方法进行了低速主射流偏转控制,初步达到了比例控制效果,实现了推力矢量化。文献[19]中以二元收扩喷管为对象,给出了主次流气动参数及几何参数对流体推力矢量喷管流场结构和性能影响的关联关系。文献[20]中通过实验和数值计算相结合的方法,研究了主流压强对矢量偏转的影响。文献[21]中概括了流体控制矢量喷管的主要技术手段,包括Coanda效应、激波诱导、反流控制、喉道偏移和主流控制方案,给出了各种方案的原理特性和发展动态。
这些研究取得了很多成果,但是这些成果主要集中于风洞实验和CFD计算结果分析方面。能够实现主射流偏转比例控制的报道甚少,工程应用方面的研究更是难以见到。
流体矢量技术在飞翼布局无人机上的工程应用面临着以下问题:① 控制参数的选取问题;② 控制反馈信号的测量问题;③ 控制器结构设计问题;④ 控制器参数整定问题。本研究在CFD数值计算的基础上,解决了控制参数的选取,控制策略,以及可工程实现的控制器参数整定[22]等问题,为流体矢量装置的控制提供了可工程实现的设计方法。
1 模型及计算方法
1.1 设计模型
本研究采用的计算模型如图1所示。该装置由三级涡轮增压航空发动机改进而成。
流体矢量喷管模型尺寸如图2所示,其中喉道宽40 cm,涵道半径22 cm。计算采用的缩比模型尺寸如图2所示。
1.2 数值计算方法
本研究计算模型采用ANSYS ICEM软件划分网格。数值计算基于ANSYS FLUENT 14.5软件,采用密度基隐式方法求解,单元空间离散是基于Roe格式的2阶迎风格式,湍流模型采用renormalization group (RNU)κ-ε二阶模型。计算工质为理想气体,采用Sutherland公式计算黏性。初始化采用FMU(full multigrid)方法,并使库朗数逐渐增大。收敛判据包括连续、动量、能量和湍流方程的残差(下降3个量级)。
1.3 性能计算公式
1) 主推力
(1)
2) 矢量力
(2)
3) 矢量角
(3)
通过计算,该设计方案在次流为零时,主流矢量角为0°(如图3),在最大次流流速下,获得了20.85°的矢量角(见图4)。
2 计算结果与讨论
2.1 落压比(NPR)对矢量角的影响
主流驱动电机可以提供1~8的NPR工况。在次流流速为80 m/s的条件下,不同NPR条件下的主流矢量角如图5所示。和大多数文献中的研究结论相似,矢量角度随NPR的增大而减小。但是,这种减小并不具有线性关系。
2.2 主次流能量比对矢量角的影响
主次流能量比是矢量角度偏转的重要影响因素,计算结果如图6所示。从图6可以看出,当次流能量小于主流能量的0.5%时,主流偏转角度随次流偏转角度迅速增加。但是,当次流能量大于主流能量1%后,主流偏转角度随次流偏转角度增加趋于平缓并达到饱和。
2.3 次流速度对矢量角的影响
次流流速是影响装置矢量角度偏转的重要因素,计算结果如图7所示。从图7可以看出,装置的矢量角度随次流流速的增加而增加。当次流流速较小时,矢量角变化量很大,类似于装置的开关效应。但是,当次流速度大于20 m/s之后,主流的矢量角随次流流速的增加而增加,并具有较好的线性关系。
从图7可知,在次流流速相同时,NPR较大的主流偏转较小,但是这种偏差不影响次流流速和矢量角之间的近似线性关系。
2.4 参数对流体角控制影响分析
根据前文的论述可知,虽然喷管的NPR可以在很大范围内影响主流的矢量角。但是,装置的矢量角随NPR的增大而减小。在实际应用中,若要增大俯仰力矩,就要增大NPR,但是NPR的增大却减小了矢量角,又不利于俯仰力矩的产生。这对矛盾在控制上是不利的。
次流和主流的能量比可以高效地调节主流的矢量角。但是,总体而言次流能量远小于主流能量,对能量比的测量和精确控制存在困难。并且,当能量比>2%以后,主流矢量角对能量比的变化不在敏感,出现控制饱和现象。
根据次流流速与主流矢量角的关系可知,主流矢量角对次流流速很敏感。当次流流速出现很小变化时,主流矢量角改变却很大。这种现象在控制上表现为系统的鲁棒性差,对参数的扰动不具备能力。但是该效应并非全无益处。开关效应可以提高装置的响应速度,快速提供俯仰力矩。在某些特殊情况下具有重要意义,如在改出尾旋、过失速机动等极端条件下的控制。当次流流速大于20 m/s后,次流和矢量角之间具有一定的线性关系,可以对装置矢量角度进行精确控制。因此,装置矢量角度控制可以通过次流流速反馈来控制。
3 建模和控制策略
根据前文的计算可知,流体矢量涡轮增压发动机(FTV)与次流流速具有一定的线性关系。因此,本研究以二次流为基本变量对FTV进行建模。
除二次流流速外,影响主流矢量角的因素还包括二次流吸入量(进气口面积S),主流能量(这里用落压比(NPR)表示)。根据试验计算结果,FTV装置的数学模型为
(4)
根据前文的计算可知,主流的矢量角对扰动很敏感,微小的扰动就会产生较大的矢量偏角。为了达到稳定控制的效果设计采用主/次流协同控制法。即偏航姿态的控制在主流工作的同时,还需上下次流以一定的流速参与控制。通过次流流速的调节,实现矢量角对各种扰动的适应能力,保持矢量角的稳定,从而提高主流矢量角的鲁棒性。
该控制策略的验证如下,当上方次流以11 m/s的速度、下方次流以10 m/s的速度工作时,主流的矢量角如图8所示。从图8可以看出,主流的矢量角基本保持了零度。该控制方案可以通过对次流的控制提高系统的鲁棒性。
俯仰通道的控制上,主要目的是实现主流矢量角和NPR的精确控制,从而产生矢量的俯仰力矩。主流矢量角和NPR的控制可以通过调节主次流的流速来实现。
4 矢量装置的控制方案
4.1 控制器结构
控制系统设计要考虑的首要问题是反馈信号的测量问题。在该系统中,可以通过空速探针获得主流、次流流速信息。但是,仅采用反馈主流和次流流速信息并不能达到对主流矢量角理想的控制效果,这就需要额外的反馈控制信号。用矢量角信息作为反馈信号控制矢量角的偏转是理想的控制方法。但是矢量角信息的直接测量是十分困难的,而壁面压力信息的测量则相对容易。因此,矢量角信号可以采用测量得到矢量力然后计算得到矢量角信号的方式。
为了实现对偏航和俯仰通道的控制,控制系统控制参数包括主、次流的流速,控制反馈信号包括主流、次流流速、主流矢量角。通过对主流流速的调节,可以实现对推力的控制。通过调节次流流速,可实现对主流矢量角的控制。
由于流体矢量装置尚没有精确的数学方程描述的模型,给控制带来了一定的困难。为达到准确的控制效果,本文采用对模型依赖较小的偏差原理思想进行系统控制系统设计。为了提高系统的鲁棒性,为系统设计了补偿器。系统控制结构如图9所示。
4.2 控制律设计
控制器包括主流流速控制和矢量角控制。其中,主流流速控制律为
(5)
由于矢量角的测量存在误差,所以以次流流速为主反馈信号,矢量角信号作为辅助,主流矢量角的控制控制律为
(6)
补偿器的控制律为
(7)
实际应用中,采样周期足够短可以用求和代替积分,后向差分代替微分的方法表示。以上控制律用如下数字离散化处理。以补偿器控制律为例,这时控制律为
(8)
式中:T为采样周期;K为采样序号。
为编程和存储方便,式(8)的增量形式为:
Δu(k)=u(k)-u(k-1)=
Kp[e(k)-e(k-1)]+KIee(k)+
KD[e(k)-2e(k-1)+e(k-2)]
(9)
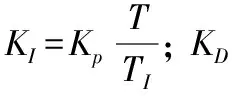
对式(9)进行整理可得:
Δu(k)=q0e(k)+q1e(k-1)+q2e(k-2)
(10)
式中:
4.3 基于粒子群(PSO)方法的参数自适应控制
用于FTV的矢量角度对参数变化敏感,这里设计了粒子群自适应控制器。PSO算法以其不要求被优化函数具有可微、可导、连续等条件,且具有思想直观、实现简单、执行效率高等优点,受到各研究领域研究者的关注[6-10]。对任意给定的非线性函数Δ:Ω→Rp,则存在常数ε>0使得Δ-W*Tφ≤ε,其中,*为向量的2范数,W*∈Rn×p为粒子群算法输出的理想权值矩阵,φ∈Rn×1为粒子群算法的输入向量,ε为算法的收敛误差。
为了提高算法的全局搜索能力和收敛速度,本文采用混沌函数对粒子初置进行初始化,确定权重系数:
(11)
(12)
其数值仿真结果如图10、图11所示。
4.4 基于试验的参数整定
由于本文建立的数学模型不够精确,这里给出另一种基于试验的参数整定方法。该方法为扩充临界比例度法对控制器参数进行整定。该方法的优点在于可以通过实验的方法弥补模型的不确定性。具体的整定步骤如下:
1) 选择一个足够短的采样周期,要求此采样周期为对空对象存滞后时间的十分之一以下。
2) 去掉控制器中的微分项和积分项,只保留比例项,用选定的采样周期使系统工作。逐渐减小比例度δ(δ=1/Kp),直到系统发生持续等幅振荡。记使系统发生持续等幅振荡的临界比例度为δcr和系统的临界震荡周期Tcr。
3) 选择控制度控制度是以模拟式控制器为基准,将数字式控制器(DDC)的控制效果与模拟式控制效果相比较。控制效果的评价函数通常用误差平方的积分表示:

(13)
式(13)描述了数字与模拟控制器的控制效果的强弱,在选择上有很大的自由性和主观性,可根据具体对象具体选取。
4) 根据选定的控制度,根据表1确定控制器参数的值。
本文根据CFD计算结果,分析了落压比、主次流能量比和次流速度对二元流体矢量装置主流矢量角的影响。计算结果显示(见表1)。
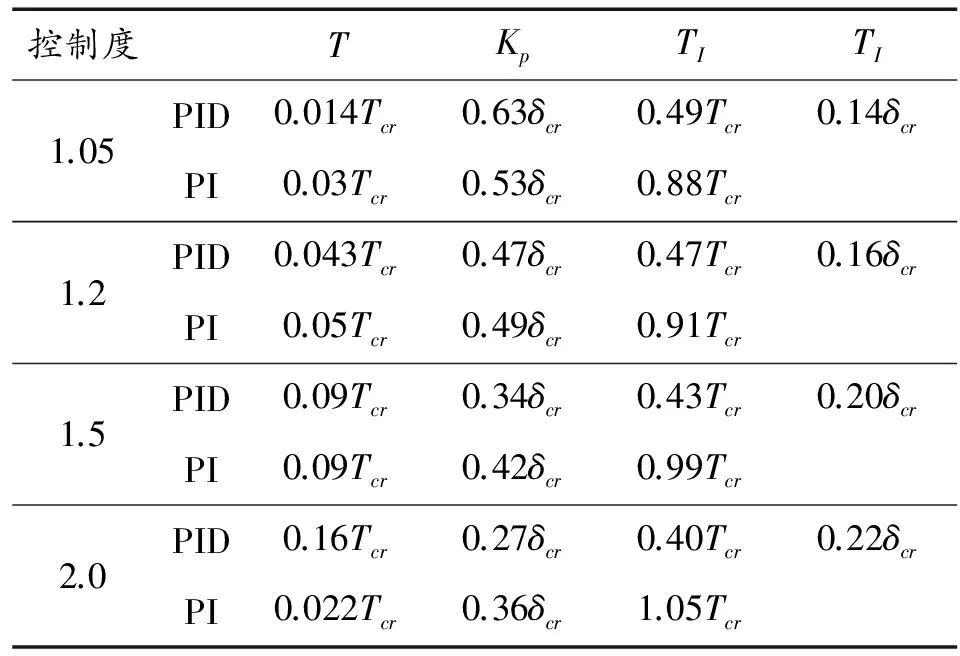
表1 扩充临界比例度法整定参数
通过调节次流的流速,主流可以获得最大20.85°的矢量角度,主流矢量角度与次流速度具有较好的线性关系,可作为主流矢量角的控制参数。
参考文献:
[1]BURSEY R,DICKINSON R.Flight test results of the F-15 SMTD thrust vectoring/thrust reversing exhaust nozzle,AIAA-1990-1906[R].Reston:AIAA,1990.
[2]HUNTER C A,DEERE K A.Computational investigation of thrust vectoring,AIAA-1999-2669[R].Reston:AIAA,1999.
[3]MASON M S,CROWTHER W J.Fluidic thrust vectoring for low observable air vehicles,AIAA-2004-2210[R].Reston:AIAA,2004.
[4]BOUGAS L,HORNUNG M.Propulsion system integration and thrust vectoring aspects Ior scaled jet UAVs[J].CEAS Aeronautical Journal,2013,4(3):327-343.
[5]PADZILLAH M H,YANG MINGYANG,ZHUGE WEILIN,et al.Numerical and experimental investigation of pulsating flow effect on a nozzled and nozzleless mixed flow turbine for an automotive turbocharger[J].ASME paper,No,GT2014-26152,2014.
[6]BRIGGS I,MCCULLOUGH G,SPENCE S,et al.Whole-vehicle modelling of exhaust energy recovery on a diesel-electric hybrid bus[J].Energy,2014,65:172-181.
[7]KATSANOS C O,HOUNTALAS D T,ZANNIS T C.Simulation of a heavy-duty diesel engine with electrical turbocompounding system using operating charts for turbocharger components and power turbine[J].Energy Conversion and Management,2013,76:71-724.
[8]BRIGGS I,MCCULLOUGH G,SPENCE S,et al.A parametric study of an exhuast recovery turbogenerator on a diesel-electric hybrid bus[J].ASME paper,No.GT2013-994492,2013.
[9]JYE T S A E,PESIRIDIS A,RAJOO S.Effects of mechanical turbo compounding on a turbocharged diesel engine[J].SAE paper,No.2013-01-0103,2013.
[10] MAMAT A M E,BIN R F,MARTINEZ-BOTAS R F,et al.Waste heat recovery using a novel high performance low pressure turbine for electric turbocompounding in downsized gasoline engines:Experimental and computational analysis[J].Energy,2015,90:218-234.
[11] KANT M,ROMAGNOLI A,MAMAT A M I,et al.Heavy-duty engine electric turbocompounding[J].Proc imechE Part D:J Automobile Engineering,2015,229(4):457-472.
[12] ANDREW J N,FERNANDO N U,JOHN Y.Performance studies of shock vector control Iluidic thrust vectoring[R].AIAA,2007-5086.2007.
[13] KAREN A D.Summary of fluidic thrust vectoring research conducted at NASA langley research center[R].AIAA-2003-3800.2003.
[14] SADIQ M U.Performance analysis and flowfield characterization of secondary injection thrust vector control(SITVC) for a 2DCD nozzle[D].Los Angeles:University of Southern California,2007.
[15] 王强.激波矢量控制喷管落压比影响矢量性能及分离区控制数值模拟[J].航空动力学学报,2015,30(3):527-538.
[16] 李志杰,王占学,蔡元虎.二次流喷射位置对流体推力矢量喷管气动性能影响的数值模拟[J].航空动力学学报,2008,23(9):1603-1608.
[17] 肖中云,顾蕴松,江雄,等.一种基于引射效应的流体推力矢量新技术[J].航空学报,2012,33(11):1967-1974.
[18] 曹永飞,顾蕴松.基于被动二次流的射流偏转比例控制[J].航空学报,2015,26(3):757-763.
[19] 王占学,王玉男,李志杰.基于激波控制的流体推力矢量喷管试验[J].推进技术,2010,31(6):751-756.
[20] 李卫强,宋文艳,罗飞腾.激波诱导控制推力矢量喷管实验及数值计算[J].航空动力学学报,2012,27(7):1571-1578.
[21] 康冠群 周燕佩.流体控制推力矢量喷管技术[J].推进技术,2015,17(4):83-87.
[22] LI Jiguang.The Attitude Decoupling Control Of The Flying Wing UAV(IEEE CGNCC)[C]//Proceedings of 2016 IEEE Chinese Guidance,Navigation and Control Conference (IEEE CGNCC2016).[S.l.]:[s.n.],2016.

