基于改进型K均值算法的尿沉渣图像分割研究

重庆邮电大学生物医学工程研究中心　程　星　李章勇　姜小明　夏　爽

1　引言

尿成渣图像的分析检查是尿常规检查中非常重要的部分，对于临床诊断泌尿系统疾病有很大帮助[1]。传统的尿沉渣检查需要在显微镜下，对尿沉渣样本图片进行人工检查，其目的是检查尿液里面各种有形成分，这些有形成分包括有颗粒管型、红细胞、白细胞、上皮组织以及从尿液中沉析出来的各种晶体[2]。由于医院每天需要分析大量的尿液，给检验人员带来极大地劳动量，容易影响其对于结果的判断，且易受主观性等因素的影响。更加重要的是，人工检查无法对所查图像进行快速、准确的定量处理，延缓了临床医生对疾病进行进一步的分析[3]。将数字图像处理技术应用在尿沉渣图像上不仅能有效降低检验人员的劳动强度，提高图像处理效率，减小主观因素带来的误差，而且能够实现对尿沉渣图像的精准的定量分析，从而提高诊断的准确性。

在尿沉渣图像中，由于病变、光照或其他原因，某些成分边缘模糊难以识别[4]。导致一些传统分割方法如阈值分割、边缘检测、分水岭等、在此类图像分割上无法获得快速精准的效果[5,6]。

本文采用Prewitt算子对预处理后的尿沉渣图像进行边缘提取。为了得到更好的效果还需要对图像进行二值化。利用尿沉渣有形成分形态和面积的不同提出一种应用于尿沉渣图像分割的改进型K均值聚类算法。

2　K均值聚类算法

2.1　传统的K均值聚类算法

K均值算法是目前最经典也是应用最为广泛的聚类算法[7]。该算法的基本思想为：在空间中K个点为中心进行聚类，以欧式距离作为相似度测度，对最靠对象归类。并通过迭代的方法，依次更新各聚类中心的值，直到得到最好的近他们的聚类结果，从而是的生成的每一个聚类类内紧凑，类间独立。

K均值算法首先需要指定一个固定的K值，该K值表示为希望从对象数据库中获得的簇的个数，然后随机选取任意K个对象作为初始簇的中心，初始地代表一个簇[8]。该算法在每次迭代中对数据集中余下的每一个对象，根据其到各个簇中心的距离将每个对象重新分配给距离其最近的簇。当考察完所有数据对象之后，该次迭代运算完成，根据结果，新的聚类中心被计算出来[9]。在一次迭代前后，如果E的值没有发生变化，说明算法已经收敛。E是聚类误差平方和函数作为聚类准则函数：

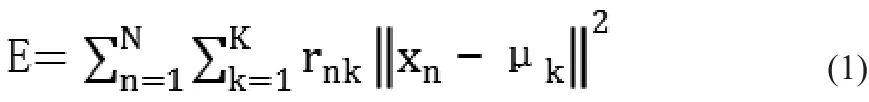
②将数据样本集合中的每一个样本按照最小距离原则分配到最邻近聚类。一般使用欧几里德距离来衡量每一个样本到不同聚类中心的距离，并将其归属到距离其最近的聚类中心；

③根据聚类的结果，重新计算K个聚类的中心：

K均值聚类算法是一种简单、快速的用来解决聚类问题的经典算法。在处理比较 大的数据集合的时候，该算法是相对可伸缩和高效率的。因为它的复杂度是0（nkt），其中，n是所有数据对象的数目，k是聚类的数目，t是迭代的次数。通常来说k ≤ n且t ≤ n。K均值算法比较适合结果簇较为密集的集合，在类与类间区别较为明显的时候，算法效果较好。

K均值缺点也较为直观，一般需要事先给出要生成的聚类的个数K，这个K值的选择非常难以预估，而且对于初始聚类点的选择很敏感，最终的聚类结果较为依赖与初始点的选择[10]。若选择不适合的数据作为聚类中心点，就很有可能导致最后结果产生误差。此外，它对于“噪声”数据和远离群点的数据较为敏感，只需少数的诸如此类的数据就可以对平均值产生很大的影响。

2.2　改进的K均值聚类算法

由于初始簇中心的的选取对于K均值聚类算法的结果影响很大，不同点作为初始簇中心可能获得不同的聚类结果，一旦选取错误的话极易导致算法生成很差的聚类结果，因此初始簇中心的选取至关重要。本文针对此问题提出一种基于传统K均值算法的改进算法，并且定义了新的函数，计算出每一个数据样本对应到此函数的值，选择让函数取得最大值的数据样本作为算法的下一个聚类中心，进而得到一种新的簇中心方法。该方法不仅可以考虑的到距离数据样本分布密集区域较为远的数据样本，也可以消除噪音点对于下一个簇中心选择的影响，从而避免了传统K均值算法的缺点。

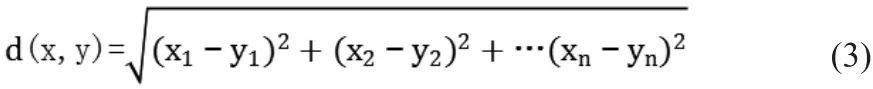
算法描述：

Step1：初始化，所有数据样本点xi，计算Di：

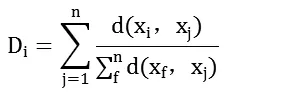
选择使得取得最小值的点当作最佳初始簇中心，并设置q=1。

Step3：通过计算寻找到下一个的簇中心，这里我们引入Ti：

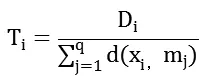
运算是的Ti取得最小值时的 数据样本xi作为下一个簇的初始聚类中心点。

Step4：判断程序终止条件，q=q+1，若q ≤ K，算法转到step2，若q＞K，则算法终止。

该算法提出了一种通过对Ti的计算来获得下一簇的最佳初始中心的方法，改进了传统K均值算法对聚类中心的选择方式，并可以准确快速的在所有数据样本中挑选出一个周围样本分布较为密集的样本作为下一簇的最佳聚类中心，并且这个中心点距离现有已存在的聚类中心都有相隔比较远的距离，这样不仅可以避免了远离数据群点的样本和噪音点对聚类结果的影响，也能够规避传统K均值算法采用随机选取簇中心的方法所带来的随机性，大大的提高了算法的准确性和可靠性。同时，本算法中引入的的计算可以让后面计算过程中避免对数据样本间距离的重复计算，极大的节省了计算机的运算时间。本算法通过对尿沉渣图像数据的实验测试表明该算法相较于传统K均值算法在处理效果和运算时间上均有所提升。

3　实验结果和分析

本文试验环境：Intel CPU，8G内存，1T硬盘，Win7操作系统，Matlab 2013平台。

实验数据来源与重庆市天海公司提供的尿沉渣图像，在实验测试中分别使用传统K均值算法与本文所提出的改进K均值算法对图像进行处理，并进行对比。在用K均值算法前，首先对图像进行预处理，经边缘检测后，利用形态学运算对图像进行孔洞填充，最后确定尿沉渣图像有形成分坐标。图2（a）、（b）分别是一些通过分割得到的红细胞和结晶。

图2　分割后的有形成分

通过对算法运算时间T和聚类误差平方和E值进行对比，证明本文所提出的改进算法相比传统的K均值算法在性能上得到较好的提升。在此选取了几幅尿沉渣图像分别用这两种方法进行处理，实验结果比较见表1所示。

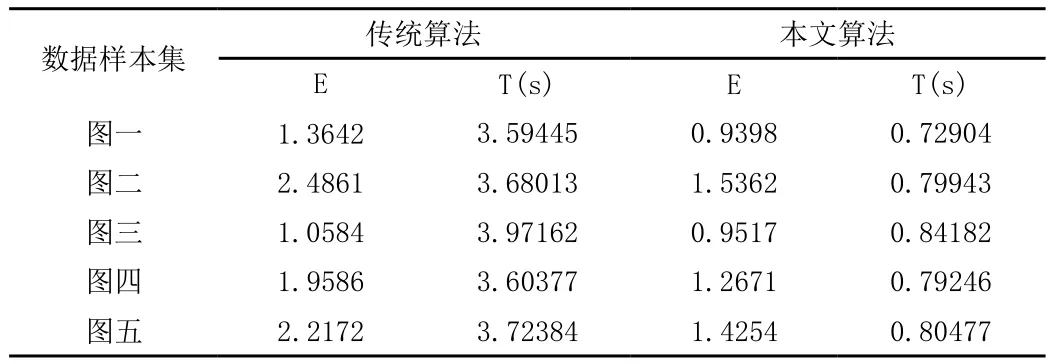
表1　不同聚类分割算法的实验结果比较

由图表1可以发现在相同图片上分别运行K均值聚类和改进型的K均值聚类算法，通过其聚类的时间T和聚类误差平方和E的比较，可以发现本文提出的改进的算法相较于传统的K均值算法不仅在准确性方面有所提升，同时也缩短了算法的运行时间。

4　结论

本文在传统K均值算法的基础上提出了一种改进型的K均值算法，针对传统算法聚类中心选取的随机不确定性和噪音点对聚类结果造成的不良影响，本文所提改进型K均值算法定义了一种新的目标函数来挑选一个距离现有已存在簇中心较远且周围样本分布较为密集的数据样本作为下一个簇的聚类中心，并选择距离所有数据样本均值最近的点作为第一个聚类的初始中心，从而解决了传统K均值算法中选取聚类中心所带来的不确定性因素和噪音点所导致的分割结果不准确的问题，进而得到了一种高效的改进型K均值算法。通过实验证明 ，改进型算法相比传统K均值算法不仅可以得到更为准确的聚类分割结果，而且在聚类时间上也要优于传统K均值算法。

[1]Aswani K C,Srinivas S.Concept lattice reduction using fuzzy K-means clustering[J].Expert System with Application,2010,37(3):2696-2704.

[2]Hassanzadeh T,Meybodi,M R.A new hybrid approach for data clustering using firefly algorithm and K-means[C].IEEE Intelligent Systems,2012:7-11.

[3]Yong-Ming L I,Zhou D, Zeng X P,et al.Research of Feature Selection of Red Cell and White Cell of Urinary Sediment Images Based on Genetic Algorithm Embedded with Multi-criteria[J].Journal of System Simulation,2008,20(14):253-282.

[4]Nath R,Jain R.Insulin Chart Prediction for Diabetic Patients Using Hidden Markov Model(HMM)and Simulated Annealing Method[C].Proceedings of the Second International Conference on Soft Computing for Problem Solving(SocProS 2012),December 28-30,2012.Springer India,2014:3-11.

[5]Erisoglu M,Calis N,Sakallioglu S.A new algorithm for initial cluster centers in K-means algorithm.Pattern Recognition Letters,2011(32):1701-1705.

[6]Saeedizadeh Z,Mehri Dehnavi A,Talebi A,et al.Automatic recognition of myeloma cells in microscopic images using bottleneck algorithm, modified watershed and SVM classifier[J].Journal of Microscopy,2016,261(1):46-56.

[7]Likas A,Vlassis M,Verbeek J.T he global K-means cluste ring algo rithm[J].P attern Recog nitio n,2003,36(2):451-461.

[8]Grigorios Tzortzis,Aristidis Likas.The min max K-means clustering algorithm[J].Pattern Recognition,2014:47(2):2505-2516.

[9]Kong Dexi,Kong Rui.A fast and effective kernel based K-Means clustering Algorithm[C].IEEE Intelligent Systems,2013:58-61.

[10]Hassanzadeh T,Meybodi,M R.A new hybrid approach for data clustering using firefly algorithm and K-means[C].IEEE Intelligent Systems,2012:7-11.

[11]Thakur P D,Patil M E.Traffic symbol recognition by means of image segmentation[J].World Journal of Science and Technology,2012,2(3):137-139．