毫米波多层交叉耦合SIW滤波器设计

南京邮电大学电子与光学工程学院　韦皓宇　钱国明

1　引言

近年来无线通信的飞速发展对通信设备的轻量化、小型化提出了更高的要求。紧凑型的微波通带滤波器（BPF）在电路中的起重要作用，其性能优劣和结构大小影响整个系统的质量。高品质因数、高功率容量、低损耗的金属波导滤波器由于体积较大，在结构紧凑的平台上应用受限。微带滤波器体积小、易集成，但损耗大、Q值低，无法满足高频电路设计要求。

基片集成波导（SIW）是于近年提出的一种新型波导结构[1]，在损耗低的介质基片边缘等间距地排列金属化通孔，并在上下底面使用金属层覆盖，在介质基片上实现传统金属波导的功能，具有矩形波导品质因数高、易设计的特性，同时具有体积小、重量轻、易集成等传统矩形不具备的优点[2]。

2　交叉耦合SIW滤波器的理论与设计

2.1　SIW谐振腔

图1 所示是一个典型的基片集成波导谐振腔。

在上下底面均为金属层的介质基片中，用金属化通孔排列在侧面构成电壁，把电磁场限制在由金属层和四周金属化孔围成的腔体中。在图1.1中，d、s分别表示金属通孔的直径和间隔。当满足：s<λ/4，s<4d时，能量泄露基本被抑制。其中，λ为介质波长。这时可把SIW腔体视为一个由介质填充的金属腔[2]，它的谐振频率可由公式(1)得出：

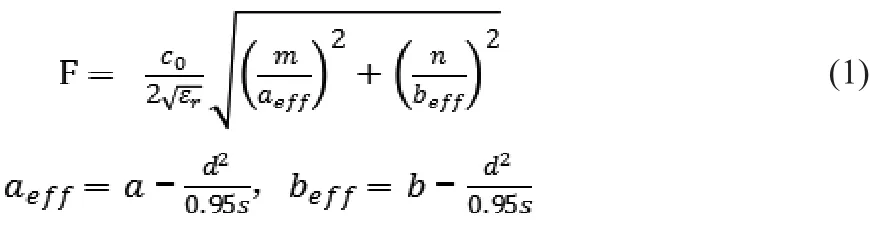
其中，aeff，beff是谐振腔的有效边长。

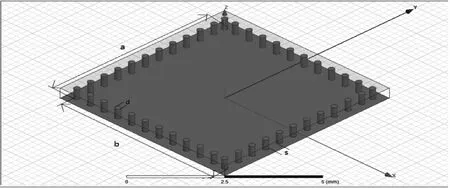
图1　基片集成波导谐振腔

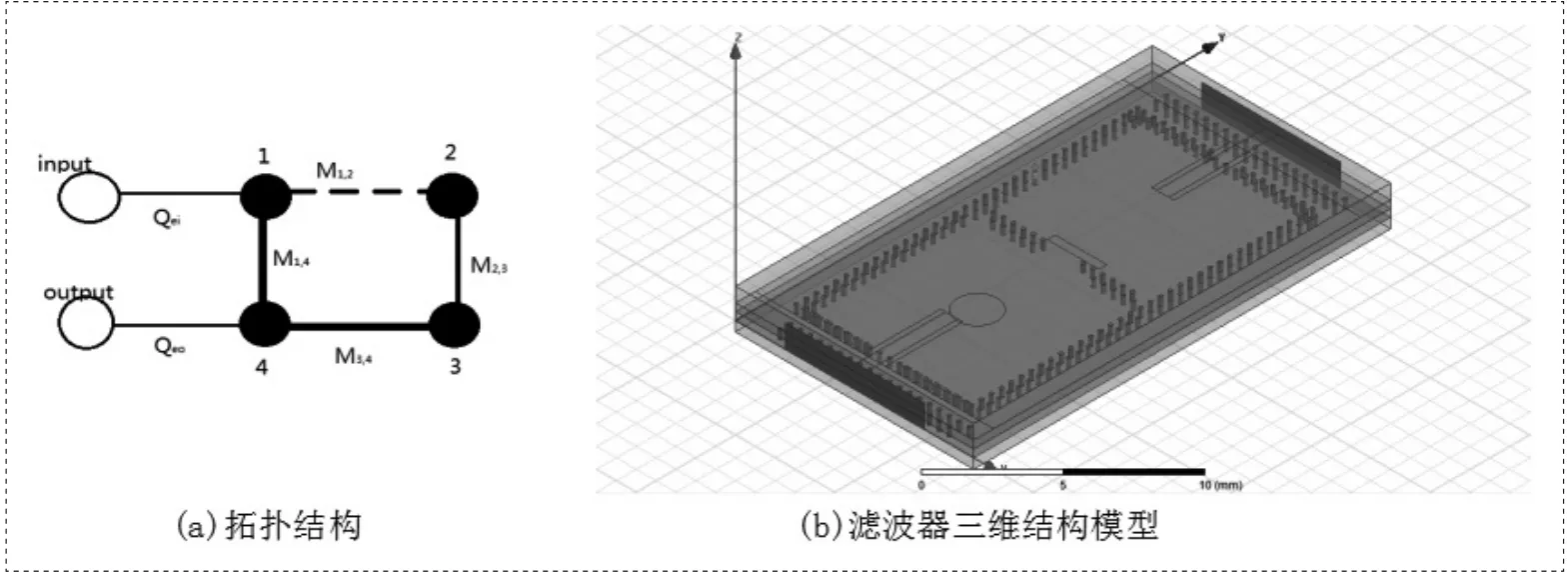
图2　四阶交叉耦合SIW滤波器

图3　外部品质因数的提取

图4　谐振腔耦合关系的提取

图5　多层交叉耦合滤波器几何参数图（单位：mm）

2.2　耦合结构

图2所示我们所设计的四级交叉耦合SIW滤波器。其拓扑结构如图a所示，图2中Mij表示第i和j级谐振器间的耦合系数。主耦合、交叉耦合分别采用实线和虚线表示。

滤波器设计目标：中心频率26GHZ，passband为25.5G～26.5G，retrun loss小于20db，通带插入损耗小于2db。

根据设计指标，使用梯度优化算法，综合得到所选拓扑结构的耦合矩阵：

外部品质因数可由以下公式计算：

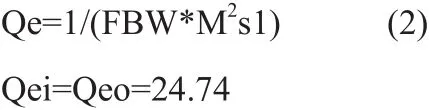
从耦合矩阵可以得到谐振腔间的耦合系数：

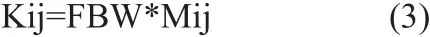
Kij反映谐振腔之间耦合关系的强弱，由连接谐振腔之间的感性或容性的槽孔尺寸决定。

传统滤波器使用解析法直接求出谐振腔和耦合结构的实际尺寸，但由于交叉耦合拓扑结构复杂，没有可供使用的解析方程直接求解。我们通过调整谐振腔间耦合结构尺寸，计算耦合系数并使之与提取出的耦合矩阵相吻合，最终满足设计要求。

外部品质因数Qe可以提取自谐振频率点反射系数的群时延[3]：

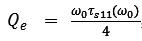
如图3所示，在仿真软件中建立电流馈针的端口谐振腔模型，改变L，W1，W2参数控制耦合强度使群时延与理论值相等，我们得到了外部耦合结构的初始尺寸。

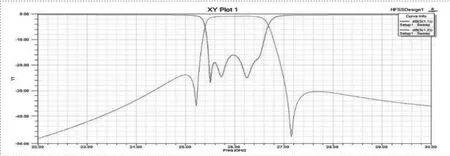
图6　多层交叉耦合SIW滤波器仿真结果

耦合矩阵中，谐振腔的耦合系数有正负之分。M23，M34，M14符号相同，他们同属磁耦合。拓扑结构中，2-3和1-4号谐振腔是两对共面的谐振腔，通过腔体公用通孔壁上的感性槽实现磁耦合。3-4是异面谐振腔，他们之间实现磁耦合的方式为在公共金属层上开出一条矩形感性槽。为实现耦合，感性槽应处于上下两谐振腔的磁场都较强的位置。

M12的负值表示电耦合。其实现方式为：在1、2腔体间的金属面上开一容性圆孔，圆孔开在两谐振腔电场较强的位置。

我们在仿真软件中建立包含耦合结构的两个相邻谐振腔，仿真模式为本征模，耦合系数可以由前两个模式的频率计算得出[4]：

其中f1、f2是谐振腔第一模式和第二模式的谐振频率。

如图4所示，通过调节感性窗的长度W和容性圆孔的半径R控制谐振腔间耦合量的大小，在相邻谐振腔的耦合系数与结构的物理参量之间建立了曲线关系。在之前提取的耦合矩阵的基础上，初步确定了各耦合结构的具体初值。

3.仿真优化

根据上文分析我们得到了由耦合矩阵确定的滤波器初始结构参数，在Ansoft HFSS仿真软件中建立模型。我们使用Ferro-A6作为基板材料，其介电常数为5.9、损耗角正切0.0015。谐振腔体的厚度为0.384mm，金属通孔直径为0.18mm。

经过优化后，模型的详细几何参数如图5所示。

仿真结果如图6所示，可以看出在25.5ghz到26.5ghz的通带内，插入损耗小于1.5db，回波损耗大于18db，上下阻带各存在一传输零点，分别位于25.2ghz和27.18ghz。

4.结论

提出了一个毫米波波段的基于SIW技术的四阶交叉耦合滤波器，采用LTCC工艺将谐振腔垂直放置，异面谐振腔之间通过容性圆孔和感性槽耦合，显著减小了电路面积。文章详细阐述了谐振腔间耦合系数的提取过程，并利用HFSS软件建模仿真，滤波器中心频率为26GHZ,在1G的通带内插损小于1.5dB。仿真结果表明该交叉耦合滤波器传输性能良好，体积紧凑，易于集成，可广泛应用于微波和毫米波系统。

[1]D.Deslandes,K.Wu.Integrated microstrip and rectangular waveguide in planar form.IEEE Microwave Wireless Compon,2001,11:68-70.

[2]X.P.Chen and K.Wu,”Substrate Integrated Waveguide Cross-Coupled Filter With Negative Coupling Structure,”in IEEE Transactions on Microwave Theory and Techniques,vol.56,no.1,pp.142-149, Jan.2008.

[3]H.J.Tang,W.Hong,J.X.Chen,G.Q.Luo and K.Wu,”Development of Millimeter-Wave Planar Diplexers Based on Complementary Characters of Dual-Mode Substrate Integrated Waveguide Filters With Circular and Elliptic Cavities,”in IEEE Transactions on Microwave Theory and Techniques,vol.55,no.4,pp.776-782,April 2007.

[4]Zhang-Cheng Hao,Wei Hong,Ji-Xin Chen,Xiao-Ping Chen and Ke Wu,”Compact super-wide bandpass substrate integrated waveguide(SIW)filters,”in IEEE Transactions on Microwave Theory and Techniques,vol.53,no.9,pp.2968-2977,Sept.2005.

[5]D.Jia,Q.Feng,Q.Xiang and K.Wu,”Multilayer Substrate Integrated Waveguide(SIW)Filters With Higher-Order Mode Suppression,”in IEEE Microwave and Wireless Components Letters,vol.26,no.9,pp.678-680,Sept.2016.

[6]D.L.Diedhiou,E.Rius,J.F.Favennec and A.El Mostrah,”Ku-Band Cross-Coupled Ceramic SIW Filter Using a Novel Electric Cross-Coupling,”in IEEE Microwave and Wireless Components Letters,vol.25,no.2,pp.109-111,Feb.2015.

[7]S.Sirci et al.,”Design and Multiphysics Analysis of Direct and Cross-Coupled SIW Combline Filters Using Electric and Magnetic Couplings,”in IEEE Transactions on Microwave Theory and Techniques,vol.63,no.12,pp.4341-4354,Dec.2015.