理想和滤子的S-收敛

潘　伟，徐振国

(1.牡丹江师范学院数学科学学院，黑龙江 牡丹江 157000； 2.国家科技基础条件平台中心，北京 100862)

1　预备知识

收敛理论不仅在拓扑和分析方面有重要的应用，在推理和其他学科中也有重要应用.文献[1]在I-拓扑中引入了具有开创性的重域概念，由此确立了完整的网的Moore-Smith收敛理论.王国俊[2]借助分子的闭远域将该理论推广到L-拓扑中.随后又出现了多种收敛理论.[3-7]文献[8]引入了半开L-集、半闭L-集和半连续映射的概念.基于文献[2]的思想，借助于文献[8]中半闭L-集概念并利用半闭远域，本文引入了理想的S-极限点、S-聚点，滤子的S-极限点、S-聚点等概念，并给出了网的S-极限点、S-聚点，理想的S-极限点、S-聚点和滤子的S-极限点、S-聚点之间的关系，确立了理想和滤子的S-收敛理论.

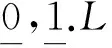
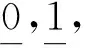
定义1.1[8]设(X，τ)是L-拓扑空间，A∈LX.则：A称为半开L-集，当且仅当A≤cl(int(A))；A称为半闭L-集，当且仅当int(cl(A))≤A.记LX中所有半开L-集的集合为SO(X)，所有半闭L-集的集合为SC(X).

定义1.2[8]令(X，τ)是L-拓扑空间，A∈LX.则：scl(A)=∧{B|B≥A，B是半闭L-集}；sint(A)=∨{B|B≤A，B是半开L-集}.

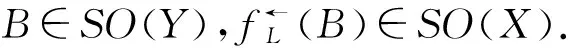
定义1.4[10]Γ⊂LX称为是X上的滤子，如果：(1)P1∈Γ，P2≥P1意味着P2∈Γ；(2)P1，P2∈Γ意味着P1∧P2∈Γ.一个滤子Γ称为超滤子，如果Γ≠0.

定义1.5[2]设(X，≤)是偏序集，a∈X，A⊂X，规定↑a={x∈X|a≤x}，↑A=∪{↑a|a∈A}.当A=↑A时，A称为上集；若对A中任意两个元素a，b，∃c∈A使得a≤c，b≤c，则称A为上定向集.对偶地，可以定义下集与下定向集.

定义1.6[2]设L是完备格，I是L的非空子集.若I是上定向集且1∈I，则称I为L中的理想基.此外若I是下集，则称I为L的理想.

2　理想的S-收敛

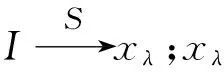
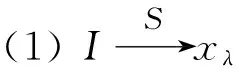
证明简单，故略去.

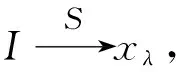
证明令P∈ηS(xλ)，则由ηS(xλ)⊂I且I是下集，有G≤P，所以xλ是G∈I的S-附着点，从而xλ≤scl(G).

证明令P∈ηS(xλ)，则ηS(xλ)⊂I，从而P∈I.因为I是下集，有G-x1≤P，所以G≤P∨xG(x).特别地，对每一个xμ∈M(IX)满足xλ≤xμ≤P，有G≤P∨xμ，因此xλ是G中S-聚点.

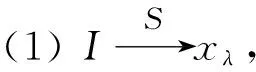
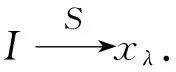
定理2.5令(X，τ)是L-空间，I是LX中理想.则limSI和adSI是半闭L-集.

该结论证明较简单，此处略去.

3　滤子的S-收敛

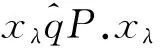
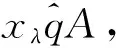
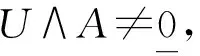
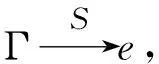
证明由于结论(2)可以由结论(1)推导出来，结论(5)和(6)的证明类似于定理2.4的证明，因此只证明结论(1)和(3).

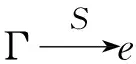
定义3.3令(X，τ)是L-空间，Γ，Φ是LX中超滤子，e∈M(LX).称Φ比Γ细(或Γ比Φ粗)，如果Γ⊂Φ.

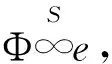
此定理的证明较为简单，此处略去.

4　网、理想和滤子之间的关系

定义4.1[10]设(X，τ)是L-空间.则：

(1) 若I是LX中理想，定义D(I)={(e，G)|e∈M(LX)，G∈I，e≤G}.对于D(I)中的点(e1，G1)，(e2，G2)，定义(e1，G1)≤(e2，G2)当且仅当G1≤G2.那么(G(I)，≤)是定向集，S(I)={S(I)(e，G)=e|(e，G)∈D(I)}是LX中的网，称为由I诱导的网.

(2) 若N是LX中网，那么I(N)={G∈LX|N最终不在G中}是LX中理想，称为由N诱导的理想.

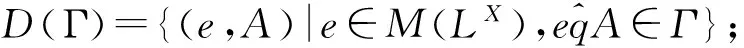
(4) 令N是LX中网，那么Γ(N)={G∈LX|N最终和G相重}是LX中滤子，称为由N诱导的滤子.

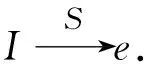
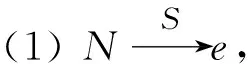
证明结论(1)的证明较简单故略去.

根据《扎赉特旗国民经济和社会发展第十二个五年规划纲要》，对2015年区域内各行业需水进行预测（见表3）。由表3可见，项目区地下水可开采量能够满足节水增粮行动项目对地下水的需求。

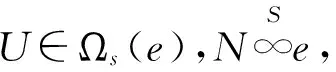
[参考文献]

[1]PU B M，LIU Y M.Fuzzy topology I：neighborhood structure of a fuzzy point and Moore-Smith convergence[J].J Math Anal Appl，1980，765：71-99.

[2]王国俊.L-fuzzy拓扑空间理论[M].西安：陕西师范大学出版社，1988：1-428.

[3]BAI S Z.Q-convergence of fuzzy nets and weak separation axioms in fuzzy lattices[J].Fuzzy Sets and Systems，1997，88：379-386.

[4]GEORGIOU D N，PAPADOPOULOS B K.On fuzzyθ-convergences[J].Fuzzy Sets and Systems，2000，116：385-399.

[5]SHI F G，ZHENG C Y.O-convergence of fuzzy nets and its applications[J].Fuzzy Sets and Systems，2003，140：499-507.

[6]YANG X F，LI S G.Net-theoretical convergence in (L，M)-fuzzy cotopological spaces[J].Fuzzy Sets and Systems，2012，204：53-65.

[7]PANG B.On (L，M)-fuzzy convergence spaces[J].Fuzzy Sets and Systems，2014，238：46-70.

[8]AZAD K K.On fuzzy semi-continuity fuzzy almost continuity and fuzzy weakly continuity [J].Journal of Mathematical Analysis and Applications，1981，82：14-32.

[9]GIERZ G，HOFMANN K H，KEIMEL K.A compendium of continuous lattices[M].Berlin：Springer Verlag，1980：1-371.

[10]ZHAO D S.TheN-compactness inL-topological spaces[J].J Math Anal Appl，1987，128：64-79.