三维Minkowski空间中的对偶直纹面

黄　杰，魏斯宁，陈　亮

(东北师范大学数学与统计学院，吉林 长春 130024)

很多学者对三维Minkowski空间中的直纹面进行了研究.[1-4]由类光直母线生成的直纹面因其特殊性，引起了几何学家的兴趣.文献[5]讨论了三维Minkowski空间中具有类光直母线直纹面的性质；文献[6]给出了三维Minkowski空间中具有类光直母线的直纹面分类.

本文主要从对偶的角度研究了三维Minkowski空间中具有类光直母线的直纹面.

1　三维Minkowski空间中的基本概念

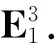
〈x，y〉=x1y1+x2y2-x3y3，

x×y=(x2y3-x3y2，x3y1-x1y3，-x1y2+x2y1).

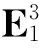
〈a×b，c×d〉=-(〈a，c〉〈b，d〉-〈a，d〉〈b，c〉).

三维Minkowski空间中的直纹面记为X(u，v)=a(u)+vb(u)，称a(u)为直纹面的导线，b(u)为直纹面的母线.特别地，如果b(u)为常向量，则称直纹面X为柱面；如果a(u)为常向量，则称直纹面X为锥面；如果a′(u)‖b(u)，则称直纹面X为a的切线面.柱面、锥面与切线面为可展直纹面，否则X为非可展直纹面.

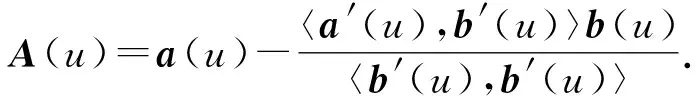
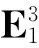
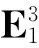
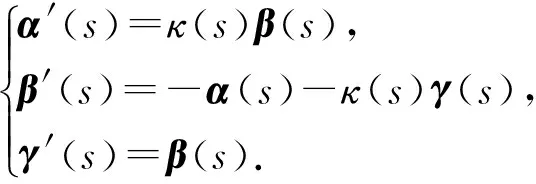
称：γ为锥曲线，{α(s)，β(s)，γ(s)}为锥Frenet标架，κ(s)为锥曲率.

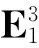
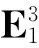
其中：a′(u)=α(u)，β(u)=b(u)×α(u)，〈β(u)，β(u)〉=1，μ是常数，λ(u)≠0.则称X(u，v)是B-scroll直纹面.

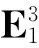
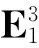
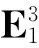
2　主要结论及证明

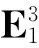
证明因为b(u)∈Q2，则有锥Frenet标架{α(u)，β(u)，b(u)}.由腰线的定义，如果导线a(u)是直纹面X(u，v)的腰线，那么〈a′(u)，b′(u)〉=0，从而〈a′(u)，β(u)〉=0.又因为〈a′(u)，α′(u)〉=〈a′(u)，κ(u)β(u)〉=0，所以a(u)也是直纹面X1(u，v)=a(u)+vα(u)的腰线.

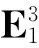
(1) 当λ≠0，μ≠0时，X(u，v)与X1(u，v)都是非退化、非可展的直纹面.

(2) 当λ≠0，μ=0时，X(u，v)是非退化、非可展的直纹面，特别地当λ=1时，X(u，v)为B-scroll直纹面；X1(u，v)是a(u)的类光切线面.

(3) 当λ=0，μ≠0时，X(u，v)是a(u)的类光切线面；X1(u，v)是非退化、非可展的直纹面，特别地当μ=1时，X1(u，v)为B-scroll直纹面.

(4) 当λ=0，μ=0时，X(u，v)与X1(u，v)都是锥面.

证明直接计算可得

以X(u，v)为例，当λ≠0，μ≠0时，因为D≠0，所以X(u，v)为非退化直纹面.又因为(a′(u)，b(u)，b′(u))=(λ(u)α(u)+μ(u)b(u)，b(u)，β(u))≠0，所以X(u，v)为非可展曲面.当λ=1，μ≠0时，a′(u)=α(u)，由B-scroll定义知X(u，v)为B-scroll直纹面.当λ=0，μ≠0时，D=0.又因为a′(u)=μ(u)b(u)，所以a′(u)‖b(u)，X(u，v)是a(u)的类光切线面.当λ=0，μ=0时，因为a′(u)=0，a(u)为常向量，所以X(u，v)是锥面.同理上述结论对X1(u，v)也成立.

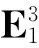
(1) 当κ(u)=μ(u)时，K1=H1；

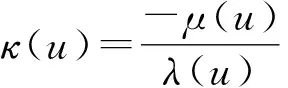
(3)X(u，v)与X1(u，v)沿着腰线a(u)的测地曲率互为相反数；

(4) 当λ，μ为常数时，腰线a(u)是X(u，v)与X1(u，v)的测地线.

证明由文献[6]知X(u，v)的高斯曲率与平均曲率分别为

同理知X1(u，v)的高斯曲率与平均曲率分别为

故结论(1)和(2)得证.

此外，直接计算可得

当λ，μ为常数时，因为沿着a(u)的测地曲率κg=0，所以a(u)是X(u，v)的测地线.同理可知a(u)也是X1(u，v)的测地线.

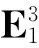
(1)X(u，v)与X1(u，v)的pitch函数δ(u)，δ1(u)不能同时为零；

(2)X(u，v)与X1(u，v)不能同为B-scroll直纹面.

证明因为b(u)∈Q2，那么有锥Frenet标架{α(u)，β(u)，b(u)}.由pitch函数定义知

δ(u)=-a′(u)·α(u)，δ1(u)=-a′(u)·b(u).

根据文献[8]定理3.2可知：δ(u)=0的充要条件为X(u，v)是腰线a(u)的副法向量面，即b(u)是a(u)的副法向量；δ1(u)=0的充要条件为X1(u，v)是腰线a(u)的副法向量面，即α(u)是a(u)的副法向量.结论矛盾，因此δ(u)和δ1(u)不能同时为0.此外，由文献[8]定理3.3知X(u，v)与X1(u，v)不能同为B-scroll直纹面.

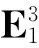
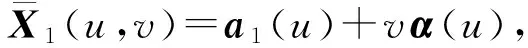
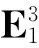
证明由null-scroll直纹面的定义，〈a′(u)，a′(u)〉=0，〈b(u)，b(u)〉=0，〈a′(u)，b(u)〉=1.又因为X1(u，v)是X(u，v)的对偶直纹面，〈α(u)，b(u)〉=1，从而α(u)‖a′(u).因此X1(u，v)不是null-scroll直纹面，而是a(u)的切线面.

[参考文献]

[1]姜扬，裴东河.三维Minkowski空间中非类光曲线的从切可展曲面的奇点分类[J].东北师大学报(自然科学版)，2007，39(1)：22-27.

[2]刘锦兰.三维Minkowski空间中非可展直纹面的分类[D].大连：大连理工大学，2008.

[3]刘作栋，姜淼鑫，陈亮.3维Minkowski空间中的特殊直纹面[J].东北师大学报(自然科学版)，2015，47(2)：1-4.

[4]王志刚，吕永震，裴东河，等.三维Minkowski空间中的特殊曲线和可展曲面[J].东北师大学报(自然科学版)，2008，40(2)：1-6.

[5]LIU HUILI.Ruled surfaces with lightlike ruling in 3-Minkowski space[J].Journal of Geometry and Physics，2009，59(1)：74-78.

[6]LIU HUILI.Characterizations of ruled surfaces with lightlike ruling in Minkowski 3-space[J].Results in Mathematics，2009，56：357-368.

[7]LIU HUILI.Curves in the lightlike cone[J].Contributions to Algebra and Geometry，2004，45(1)：291-303.

[8]GRAVES LARRY K.Codimension one isometric immersions between Lorentz spaces[J].Trans Amer Math Soc，1979，252：367-392.

[9]LIU HUILI，YUAN YUAN.Pitch functions of ruled surfaces and B-scrolls in Minkowski 3-space[J].Journal of Geometry and Physics，2012，62(1)：47-52.