小世界网络模型分析和算法模拟

葛伟伦，房丙午

当前对复杂网络的研究引起了各国学者的高度关注和重视，复杂网络是对现实世界复杂系统的抽象和概括，该网络是由大量节点相互连接而成，网络规模大，网络拓扑结构复杂且动态变化.现实生活中的人际关系网、因特网、万维网、电子邮件网、食物链网等都属于复杂网络.把各种类型的复杂网络抽象成具体模型是研究复杂网络最好的方式，近年提出的小世界网络模型能真实深刻地揭示复杂网络背后隐藏的客观规律和属性特征［1-2］.

1　小世界网络模型

1998年Watts、Strogat提出的WS小世界网络模型和Newman、Watts提出的改进NW小世界网络模型能真实反映复杂网络的特征与规律［3-4］.WS小世界网络模型建模过程：从某个含有N个节点的规则环状网开始，m为节点的度且为偶数，每个节点都与它左右邻接的各m/2个节点相连，然后进行随机化重连，将边的一个端点保持不变，另一个端点随机选择规则网中的另一个节点进行连接，满足节点之间只有一条边，并去除自连接.在WS小世界网络模型中，p=0对应于完全规则网，p=1则对应于完全随机网，通过调节p的值可以控制从完全规则网到完全随机网的变化，如图1所示.

图1　随机化重连

Newman和Watts进一步提出了NW小世界网络模型，该模型用随机化加边取代WS模型的随机化重连，避免了构造过程孤立节点的产生.NW小世界网络模型建模过程：从某个含有N个节点的规则环状网开始，m为节点的度且为偶数，每个节点都与它左右邻接的各m/2个节点相连，然后进行随机化加边，以概率 p在随机选取的一对节点之间加上一条边，满足节点之间只有一条边，并去除自连接.NW小世界网络模型中，p=0对应于完全规则网，p=1是规则网和随机网的叠加，如图2所示.

图2　随机化加边

2　小世界网络特征统计量分析［5-6］

2.1　最短路径平均长度

最短路径平均长度是小世界网络重要的特征值，这里最短路径指的是从一节点到另一节点经过的边的最小数目，整个网络最短路径平均长度为所有节点最短路径长度的平均值.设N为节点数，di,j为两个不同节点间的最短路径长度，最短路径平均长度Lavg的计算公式为：

2.2　集聚系数

集聚系数是反映小世界网络集团化程度的特征量，集团中的成员相互紧密联系，依赖性强.节点i的集聚系数能表示网络中与该节点直接相连接的其他节点之间的连接紧密度，ki表示与节点i直接连接的节点数，ei表示与节点i相连接的节点间实际存在的连接边，ki(ki-1)/2表达式为ki个节点间理论上存在的最大连接边，则节点i的集聚系数Ci表示为：

则整个网络的集聚系数C定义为所有节点集聚系数的平均值，表示为：

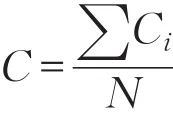
3　小世界网络模型的算法模拟和分析［7-8］

3.1　算法描述

根据上文分析，以WS小世界网络模型为例设计算法实现模拟，首先假设一个环状规则网络有N个节点，每个节点与最近邻的k个节点相连，本次模拟网络规模较小，设置N=20，k=4，不改变边和节点的数目.重连概率用随机函数产生一个0到1之间的随机数θ来表示，θ=rand（），假设随机化重连的概率为0.1，当产生的随机数θ＜0.1就进行重连，否则不重连；重连过程中随机选择重连对端节点，通过随机函数产生一个在1到N范围内的随机整数m，表达式为1+int（rand（）*（N-1）），m 代表随机重连的节点编号，若m恰好等于原节点编号，就重新产生一次，即再产生一个随机数.算法如下.

首先，随机选择一个节点，当θ＜0.1时按顺时针方向把连接它和它最近的那个节点的边重新连接到环状网上的其他对端节点，对端节点编号随机产生，θ＞=0.1不进行重连.

然后，同样按顺时针方向把连接它和它第二近的那个点的边以随机概率θ是否大于0.1判断是否重新连接到环状网上的其他对端节点，重复此过程直到此节点的所有边都按随机概率θ大小重新遍历一遍.

最后，轮换到下一个节点重复（1）和（2）步骤，直至N个节点都按相同方式遍历所有节点结束.

3.2　算法代码实现

（1）通过以下算法代码生成规则环状网，如图3所示，矩阵中“1”表示有边连接两个不同节点，”0”表示无边连接节点.

//以下代码实现规则边

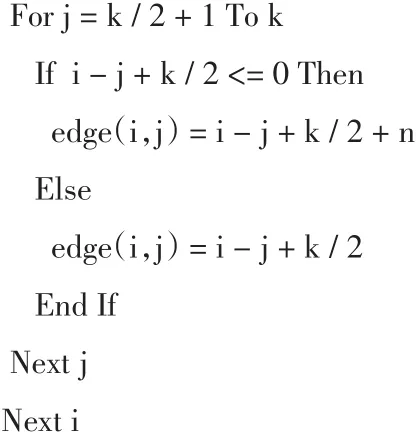
//以下代码实现规则矩阵

图3　N=20，k=4规则环状网

（2）通过以下算法代码使用随机化重连生成小世界网络模型，如图4所示.观察矩阵，可看出其中一些边在满足概率p条件下已经重新连接，不过因为重连的概率（p＜0.1）不大，所以很多边保持不变，这使得每个节点与其周围邻居节点关系较规则网络变化不大，聚类系数仍然保持在一个较大的数值，但因为生成了一些长路径加强了远距离节点的连接，从而使得整个小世界网络最短路径平均长度明显减小.

图4　N=20小世界网络模型

（3）通过以下算法代码统计小世界网络模型最短路径平均长度.

（4）通过以下算法代码统计小世界网络模型聚类系数值.

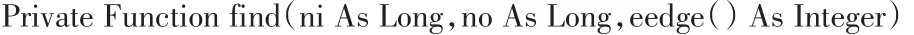
3.3　统计数据分析

本次网络规模较大，取节点数N=1000，每个节点的度k=20，依据上面统计特征值代码计算规则环状网的最短路径平均长度L=50.45045，聚类系数C=0.6666667.现在以15个不同的概率P从小到大进行随机化重连构建WS小世界网络模型，依据上文算法计算最短路径平均长度和聚类系数值，对每次取的概率P模拟运算20组数据求出统计量平均值，概率P、平均聚类系数avsc、最短路径平均长度avsl如表1所示.可以看出随着随机化重连概率P的增加，连接节点的长路径增多，使最短路径平均长度从44.83816急剧减小4.413377，但聚类系数缓慢变小，变化幅度从0.6663419缓慢减小到0.4872532，完全符合复杂网络的小世界特性和高聚类特性.

对最短路径平均长度和聚类系数进行归一化处理，获得的统计结果如图5所示，图中L（P）和C（P）表示以不同的概率 p得到的小世界网络平均最短路径长度和聚类系数，L（0）和C（0）表示规则环状网的最短路径长度和聚类系数，用L（0）和C（0）对L（P）和C（P）进行归一化处理.展示了最短路径长度和聚类系数随概率P变化的曲线图.可以得出这样结论：在概率P处于0.01～0.02附近，最短路径平均长度已经很小，但聚类系数仍然很大，符合小世界网络特征，现实世界中很多复杂网络系统从诞生、形成、发展和消失和算法模拟生成的小世界网络特征和规律完全吻合［9］.

表1　P和avsc、avsl的平均值

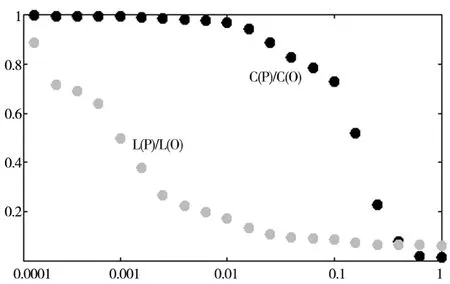
图5　最短路径平均长度和聚类系数随P变化情况

4　结语

对WS和NW小世界网络模型建模过程进行分析，并阐述了最短路径平均长度和集聚系数特征值的意义，基于一个规则环状网设计算法和代码模拟了小世界网络模型的形成，并解决了重连概率θ和对端节点选择的随机产生问题；并设计和运行代码获得最短路径平均长度和集聚系数特征值的统计数据，验证和分析了小世界网络的内在特性，使模拟大规模的小世界网络成为可能.

参考文献：

［1］王小帆，李翔，陈关荣.复杂网络理论及应用［M］.北京：清华大学出版社，2006.

［2］周涛，张子柯，等.复杂网络研究的机遇和挑战［J］.电子科技大学学报，2014，43（1）：1-5

［3］程学旗，沈华伟.复杂网络的社区结构［J］.复杂系统与复杂性科学，2011，8（1）：57-66.

［4］郭雷，许晓鸣.复杂网络［M］.上海：上海科技教育出版社，2010.

［5］刘常昱，胡晓峰，司光亚，等.基于小世界网络的舆论传播模型研究［J］.系统仿真学报，2006，18（12）：3608-3611.

［6］李果，高建民，高智勇，等.基于小世界网络的复杂系统故障传播模型［J］.西安交通大学学报，2007，41（3）：334-338.

［7］王波，王万良，等.WS和NW两种小世界网络模型的建模及仿真研究［J］.浙江工业大学学报，2009，37（2）：179-188.

［8］杨晓光，朱保平.基于复杂网络的社区发现算法［J］.南京理工大学学报，2016，40（3）：267-271.

［9］肖维民，张赛.k错线性复杂度的分布研究［J］.吉林师范大学学报，2016（2）.