一种半球谐振陀螺谐振子动力学建模方法

徐泽远，伊国兴,，魏振楠，赵万良

1. 哈尔滨工业大学 航天学院，哈尔滨 150001 2. 上海航天控制技术研究所，上海 201109

半球谐振陀螺(HRG)是一种新型的高精度、高稳定性、长寿命的固体振动陀螺[1-4]，非常适合长时间工作场合的使用，在航空航天领域的应用越来越广泛[5-6]。与机械陀螺、光纤陀螺和激光陀螺等相比[7-9]，它结构简单，无损耗部件(如机械转子和光源等)，无需后期维护；不需预热，启动时间短；功耗低，体积小，重量轻；具有很强的抗冲击能力，能承受大的机动过载；抗辐照能力强，失效因素少；谐振子物理特性稳定，陀螺具有很高的可靠性和超长的寿命，连续工作15年的可靠度高达0.99，这些优点使得半球谐振陀螺在惯性技术领域具有广阔的应用前景，为此发展半球谐振陀螺技术对于中国导航技术的快速发展具有十分重要的意义。

目前，半球谐振陀螺误差机理分析与抑制技术仍是制约其发展的关键因素之一。而建立半球谐振陀螺谐振子的动力学模型为研究其误差机理问题提供了力学基础。所以，在半球谐振陀螺的理论研究和实际制造过程中，其误差机理分析的基础是含有各种误差源的半球壳谐振子动力学模型，这些误差源包括谐振子的密度不均匀、厚度不均匀、品质因数不均匀等加工工艺误差和温度、加速度等环境因素的影响[10-16]，还可用于研究电极的加工误差及其不同控制方式对陀螺精度和性能的影响[17-19]。

对于谐振子的动力学建模一直在不断地完善，目前的谐振子动力学模型主要对谐振子的唇缘处进行动力学建模，将半球壳谐振子简化成环形谐振子，解算的动力学参数偏差较大，这是因为只是单纯地分析了变形最大的谐振子边缘处的振动特性，而谐振子是整体振动，必须对整个谐振子的振动特性进行分析。另外，有的研究虽然是对整个谐振子进行建模，但是在推导谐振子中面物理方程过程中，对中面内力作了简化，直接影响所建立动力学方程的精度；在外载荷加载过程中，将外载荷进行简化，以致不能准确地反映其实际作用效果，建立的动力学模型精度较低。

针对以上问题，本文在现有的谐振子动力学模型基础上进行了改进，基于弹性力学薄壳理论，提出了一种完善的谐振子动力学建模方法，结合谐振子的整体动力学分析，推导了更完整的谐振子动力学方程，利用布勃诺夫-伽辽金法建立了更精确的谐振子2阶谐振状态动力学模型。谐振子动力学模型参数的计算值与测试数据结果一致，证明了本文提出的谐振子动力学建模方法的正确性。建立的谐振子动力学模型能更全面地用于半球谐振陀螺误差机理问题研究。

1 半球谐振陀螺简介

1.1 半球谐振陀螺工作原理

力反馈式半球谐振陀螺的组成结构主要由外基座、谐振子和内基座三件套构成，如图1(a)所示。外基座的内表面均匀分布激励电极，用于谐振子的振幅、速率、正交以及频率控制。陀螺内基座的外表面均布检测电极，用于谐振子谐振频率、振幅、振型角和正交漂移等振动状态的检测。下面简单介绍核心部件谐振子的工作原理。

谐振子如图1(b)所示，它由高纯熔融石英制成，并在其表面喷镀金属薄层，用以构成电极的一个电极板。谐振子工作于2阶谐振状态下，其半球壳唇缘处振动驻波为四波腹形式，如图2(a)所示。振动过程中，唇缘变形达到最大时为椭圆形，椭圆的长轴称为波腹轴。四波腹状态下存在2个相互正交的波腹轴。2个椭圆存在4个交点，即为波节点。波腹轴位置用于谐振子的振幅控制和检测振幅信息，波节点位置用于谐振子的速率控制和检测振型角信息。

当谐振子敏感轴方向有外界角速度Ω输入时，谐振子的振型会相对于初始位置发生进动，进动角度ϑ称为振型角，如图2(b)所示。理论和实验都可以证明，在2阶谐振状态下，ϑ与Ω的关系为

(1)

式中：K为谐振子的比例系数。

式(1)说明，只要测量出谐振子的2阶振型角，就可以得到谐振子相对于惯性空间转过的绝对角度。

基于以上分析可知，对谐振子进行动力学分析与精确建模是十分必要的。表1为谐振子的几何参数(如图1(b)所示)与物理参数。

表1 谐振子的几何参数与物理参数Table 1 Geometry and physical parameters of resonator

1.2 谐振子的半球壳模型

在建模过程中，将半径为R、厚度为h的伞形谐振子结构简化为半球形进行建模，以半球壳中面的曲率线为θ、φ坐标线，如图3所示。图中： 以谐振子球心为原点，定义谐振子坐标系Oxryrzr。

2 谐振子动力学特性分析

2.1 薄壳的弹性力学几何方程

薄壳的厚度h远小于壳体中面的最小曲率半径R，谐振子符合薄壳的条件。在薄壳的弹性力学几何方程基础上建立半球壳谐振子动力学模型。为建立符合谐振子振动特性的薄壳弹性力学几何方程，在基希霍夫-李雅夫假设基础上作出如下基本假设：

1) 垂直于中面的正应变可以忽略不计。

2) 变形前任何垂直于中面的法线在变形后仍然垂直于中面，而且中面法线及其垂直线段之间的直角保持不变，即该方向的切应变为零。

3) 与中面平行截面上的正应力远小于其垂直面上的正应力，因而它对应变的影响可以忽略不计。

4) 薄壳上所有加载的面力均可转化为作用于中面的载荷。

谐振子中面内任意一点P0的位移在θ、φ和γ坐标方向的分量分别用p1、p2和p3表示，沿坐标轴方向的正应变用τ1、τ2和τ3表示，切应变用τ23、τ31和τ12表示。点P0发生位移后到达Q0点，Q0点的坐标为θ+dθ、φ+dφ和γ+dγ。建立中面应变与中面位移关系的几何方程，在任意一点P0处取一个体积微元，体积微元的所有边都沿着坐标线θ、φ和γ的方向，如图4所示。

当坐标改变时，θ线的弧长增量与θ坐标增量的比值称为θ方向的拉梅系数H1[20]。同理定义φ方向的拉梅系数H2,γ方向的拉梅系数H3。其中γ为直线坐标，直线的拉梅系数为1。

(2)

式中：k1和k2分别为P0点沿θ和φ方向的曲率，且

(3)

其中：x、y和z为直角坐标，对应下文中的半球壳谐振子坐标系。

将应变分量用位移分量来表示，首先计算薄壳中面的正应变，以P0P1的正应变τ1为例。边P0P3与P1Q2的交角为dη13，边P0P1在θγ面的曲率半径为R13,P0P1在θφ面的曲率半径为R12，且

(4)

(5)

(6)

应用式(4)～式(6)可得正应变为

(7)

其次来考虑切应变，以直角∠P1P0P2的切应变τ12为例。此项切应变是由P0P1和P0P2在θφ面内相向的转角相加而成，推导过程同上，可得

(8)

由以上推导过程，同理可得弹性力学几何方程的6个表达式为

(9a)

(9b)

(9c)

(9d)

(9e)

(9f)

建立谐振子动力学方程的过程中以半球壳的中面位移、中面应变、内力以及中面载荷作为讨论对象。下面将以弹性力学几何方程式(9)为基础推导半球壳谐振子的变形几何方程、物理方程和平衡微分方程。

2.2 半球壳谐振子变形的几何方程

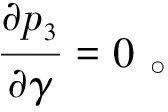
p3=w

(10)

令面上各点沿θ和φ方向的位移分别为u和v，即

(11)

根据2.1节中的第2)个基本假设，采用正交曲线坐标系，有τ31=0和τ23=0。根据式(9d)和式(9e)，利用式(2)，以w代替p3，并对γ从0到γ进行积分，注意w不随γ变化，求解p1和p2，简化以后，与式(10)联立可得：

(12)

在半球壳中，γ的最大绝对值是h/2，可见k1γ和k2γ的最大绝对值分别为k1h/2和k2h/2，与1相比，是很小的数值。在文献[20]中，计算精确到1阶小量，1+k1γ和1+k2γ可以用式(13)所示的展开式来代替，达到提高建模精度的目的。

(13)

然后，将式(2)、式(12)、式(13)代入式(9a)、式(9b)和式(9f)，化简得

(14)

式中：

(15)

式(15)表明中面应变与中面位移之间关系的方程就是半球壳谐振子变形的几何方程。

2.3 半球壳谐振子的物理方程

在θ面上(在θ为常量的横截面上)，作用于中面单位宽度上的法向力用T1表示，剪力用T12表示；同样，在φ面上(在φ为常量的横截面上)，法向力为T2，剪力为T21；以上4个力称为半球壳谐振子的中面内力，如图5(a)所示。在θ面上，作用于单位宽度上的弯矩用M1表示，扭矩用M12表示，横向剪力用S1表示；在φ面上，弯矩用M2表示，扭矩用M21表示，横向剪力用S2表示；以上6个力称为弯曲内力，如图5(b)所示。

通过分析计算得出中面内力及弯曲内力为

(16)

2.4 半球壳谐振子的平衡微分方程

下面建立表述半球壳谐振子中面的内力与所受载荷之间关系的平衡微分方程。考虑任意微分壳体OO1O3O2的平衡，如图6所示。在图6中，把中面内力和横向剪力画在一个图中，如图6(a)所示；而把弯矩和扭矩画在一个图中，如图6(b)所示，图中的X、Y、Z是单位中面面积范围内的载荷。

首先分析了各力在OO1θ轴上的投影，从而建立平衡微分方程∑(T+S)θ=0，将相关的投影分量相加，令总和等于零，再进行微分，得到平衡微分方程∑(T+S)θ=0的投影方程。同理可得∑(T+S)φ=0和∑(T+S)γ=0的平衡微分方程。将所有的力对OO1θ、OO2φ和Oγ求矩，得到∑Mθ=0、∑Mφ=0和∑Mγ=0的平衡微分方程，建立的平衡微分方程为

(17a)

(17b)

ABZ=0

(17c)

(17d)

(17e)

(17f)

3 谐振子动力学方程

3.1 谐振子的半球壳模型

1) 谐振子坐标系

以谐振子球心为原点，定义谐振子坐标系Oxryrzr，如图7所示。谐振子上点Q的矢径q可以表示为

q=xxr+yyr+zzr

(18)

式中：xr、yr和zr为谐振子坐标系的单位矢量；矢径q的坐标值x、y和z表达式为

(19)

2) 谐振子中面一点沿θ和φ方向的拉梅系数为

(20)

3) 任意一点沿θ和φ方向的曲率半径为

R1=R2=R

(21)

4) 当谐振子中面发生形变时，Q(θ,φ,R)变形之后到达Q′，产生的位移矢量W在局部坐标系(t1t2n系)中的表达式为

W=ut1+vt2+wn

(22)

5)xryrzr系与t1t2n系的转换关系为

(23)

3.2 谐振子动力学方程

由于求解式(15)～式(17)这3个偏微分方程组的难度很大，故而采用谐振子中面不可拉伸的假设[23]，谐振子中面上的正应变和切应变等于零，满足

ε1=ε2=ε12=0

(24)

为了分析半球谐振陀螺谐振子的振动特性，必须要分析其位移分量，因此以位移分量表示谐振子动力学方程。将谐振子的半球壳模型参数式(18)～式(23)及中面不可拉伸的假设式(24)代入式(15)～式(17)后化简，并将式(15)～式(17)联立可得谐振子动力学方程为

(25)

由式(25)可知，该式能用于建立含有中面半径R不均匀、厚度h不均匀的动力学方程。式(25)是在现有动力学方程基础上进行改进建立的更精确的谐振子动力学方程，体现在以下4个方面：

1) 更全面的动力学分析

在建立物理方程时考虑了曲率改变量和扭率改变量，对物理方程中内力的分析更加完善，有利于建立更精确的动力学方程。

在建立谐振子动力学方程方面，现有的动力学方程在谐振子唇缘处进行动力学建模，将半球壳谐振子简化成环形谐振子，不能全面地描述谐振子的振动特性。为解决这一简化问题，动力学方程式(25)描述了整个半球壳的振动特性，可以得到半球壳任意θ∈[0,π/2]的动力学方程。

2) 更完整的半球壳谐振子动力学建模

在加载外载荷方面，动力学方程式(25)没有将外载荷近似简化加载在谐振子唇缘处，而是在建模过程中，保留了外载荷的实际作用效果，有利于反映谐振子的实际振动特性，可以加载求解得到更精确的谐振子2阶谐振状态动力学模型。

3) 有利于建立更准确的激励电极模型

因为激励电极是分布在θ∈[75°,85°]、φ∈[0°,360°]上的一个独立区间，而不是谐振子边缘上的一个点，进行激振力的加载时是作用在整个激励电极上的，而不是作用在谐振子的边缘上，可以更准确地进行激振力的加载，对于后续控制系统激励电极的建模很有意义。

4) 更方便求解外载荷的影响

动力学方程式(25)是线性偏微分方程组，外载荷分析满足叠加原理，可对不同形式的外载荷进行单独分析。

4 谐振子2阶谐振状态动力学模型

4.1 布勃诺夫-伽辽金法求解

谐振子处于工作状态时，不考虑外界加速度和温度的影响，作用在谐振子上的惯性载荷为

(26)

考虑加速度和温度等外界环境因素的影响时，对谐振子的影响主要通过式(26)体现，由此可以分析环境因素通过影响谐振子从而导致的陀螺漂移机理。

谐振子在2阶谐振状态时，环向波数为n的变形方程满足瑞利里茨函数为

(27)

式中：振型方程W2=-[(2+cosθ)tan2θ]/2,U2=V2=(sinθtan2θ)/2；ω2为2阶谐振角频率；t为时间；p(t)和q(t)为与时间相关的系数。

由文献[23]可知，当谐振子进入2阶稳态振动时，p(t)和q(t)近似满足

(28)

式中：a和b为与谐振子振幅相关的系数。

本文利用布勃诺夫-伽辽金法求解近似解析解，过程为

L=ut1+vt2+wn=[(U2cos 2φ)t1+(V2sin 2φ)

t2+(W2cos 2φ)n]p(t)+[(U2sin 2φ)t1-

(V2cos 2φ)t2+(W2sin 2φ)n]q(t)=

L1(x)p(t)+L2(x)q(t)

(29)

将式(26)～式(28)代入动力学方程式(25)中，并用Ax、Ay和Az分别表示动力学方程组的3个式子，则半球壳谐振子边缘的运动方程M可表示为

M=Axt1+Ayt2+Azn=0

(30)

由布勃诺夫-伽辽金法方法得：

(31)

式中：Vhs为半球壳区域，化为球坐标，可得半球壳谐振子的2阶固有振型动力学方程为

(32)

求解结果为

(33)

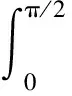
(34)

其中：

(35)

(36)

(37)

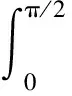
(38)

建模过程中必须考虑到实际谐振子中存在材料内摩擦，模型应该是一个具有衰减环节的2阶系统，因此在模型中加入阻尼比ξ2，将方程写成标准形式为

(39)

式中：ξ2=1/(Qfω2)。

考虑谐振子的材料内摩擦，由式(39)可得带有品质因数的p(t)和q(t)表达式为

(40)

由式(32)、式(39)和式(40)可知，能建立含有密度ρ不均匀、品质因数Qf不均匀的动力学方程，以此为基础分析加工工艺误差对陀螺的影响。

4.2 测试验证

将表1中参数代入文献[21]中的动力学模型，求解出的比例系数和2阶谐振频率为K≈0.313,f2≈2 578.0 Hz。将表1中参数代入文献[22]中得到比例系数为K≈0.277。文献[23]中动力学模型求解得到的比例系数和2阶谐振频率为K≈0.277,f2≈10 269 Hz。

与文献[21-23]中的比例系数和2阶谐振频率的结果相比，本文比例系数、2阶谐振频率的解算结果与实际测试结果基本一致。

5 结 论

针对半球谐振陀螺谐振子动力学建模的实际应用问题，基于弹性力学薄壳理论，提出了完善的谐振子动力学建模方法，为其他振动类陀螺的动力学建模提供了理论基础。

1) 在弹性力学几何方程的基础上，推导了谐振子的变形几何方程、物理方程以及平衡微分方程，建立了精确的谐振子动力学方程，给出了动力学方程建立过程中相关问题的处理方法。

2) 与现有的动力学方程相比，建立的谐振子动力学方程更准确、更有优势，主要体现在：① 更全面的动力学分析；② 更完整的半球壳谐振子动力学建模；③ 有利于建立更准确的激励电极模型；④ 更方便求解外载荷的影响。

3) 通过半球谐振陀螺谐振子的参数计算和实际测试结果的对比验证，结果一致，证明建立了准确的谐振子动力学模型。

4) 建立的谐振子动力学方程为以后研究谐振子的中面半径不均匀、密度不均匀、厚度不均匀、品质因数不均匀等加工工艺误差以及加速度、温度等环境因素导致的陀螺误差机理问题提供了动力学基础。

参 考 文 献

[1] ROZELLE D M. The hemispherical resonator gyro: From wineglass to the planets[C]∥Proceeding 19th AAS/AIAA Space Flight Mechanics Meeting. Reston, VA: AIAA, 2009: 1157-1178.

[2] XU Z Y, YI G X, QI Z Y, et al. Structural optimization research on hemispherical resonator gyro based on finite element analysis[C]∥The 35th Chinese Control Conference. Beijing: Technical Committee on Control Theory, Chinese Association of Automation, 2016: 5737-5742.

[3] MATTHEWS A, RYBAK F J. Comparison of hemispherical resonator gyro and optical gyros[J]. IEEE Aerospace and Electronic Systems Magazine, 1992, 7(5): 40-46.

[4] MEYER A D, ROZELLE D M. Milli-HRG inertial navigation system[C]∥The IEEE/ION Position, Location and Navigation Symposium (PLANS’12). Piscataway, NJ: IEEE Press, 2012: 24-29.

[5] ZHBANOV Y K. Vibration of a hemispherical shell gyro excited by an electrostatic field[J]. Mechanics of Solids, 2008, 43(3): 328-332.

[6] ZHBANOV Y K. Self-tuning control loop for suppression of quadrature in a hemispherical resonator gyro[J]. Gyroscopy and Navigation, 2007(2): 37-42.

[7] 王锦瑜, 冯培德. 激光陀螺速率偏颇系统的分析研究[J]. 航空学报, 2001, 22(1): 46-50.

WANG J Y, FENG P D. Research on rate-bias system of laser gyro[J]. Acta Aeronautica et Astronautica Sinica, 2001, 22(1): 46-50 (in Chinese).

[8] 李金涛, 房建成. 高精度光纤IMU的磁屏蔽方法及实验研究[J]. 航空学报, 2011, 32(11): 2106-2116.

LI J T, FANG J C. Magnetic shielding method and experiment study of inertial measurement unit based on high precision fiber-optic gyroscope[J]. Acta Aeronautica et Astronautica Sinica, 2011, 32(11): 2106-2116 (in Chinese).

[9] 魏玉淼, 董永贵, 李昊. 微机械陀螺非线性特性的自由衰减振荡测量方法[J]. 仪器仪表学报, 2016, 37(11): 2465-2472.

WEI Y M, DONG Y G, LI H. Free damped oscillation measurement method for the nonlinear features of micromechanical gyroscopes[J]. Chinese Journal of Scientific Instrument, 2016, 37(11): 2465-2472 (in Chinese).

[10] 李巍, 任顺清, 王常虹. 半球谐振陀螺谐振子品质因数不均匀引起的误差分析[J]. 航空学报, 2013, 34(1): 121-129.

LI W, REN S Q, WANG C H. Analysis for impact of resonator’sQ-factor nonuniformity on the error of hemispherical resonator gyro[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(1): 121-129 (in Chinese).

[11] SHATALOV M Y, JOUBERT S V, COETZEE C E. The influence of mass imperfections on the evolution of standing waves in slowly rotating spherical bodies[J]. Journal of Sound and Vibration, 2009, 330(1): 127-135.

[12] ZHBANOV Y K. Amplitude control contour in a hemispherical resonator gyro with automatic compensation for difference inQ-factors[J]. Mechanics of Solids, 2008, 43(3): 328-332.

[13] SHATALOV M Y, COETZEE C E. Dynamics of rotating and vibrating thin hemispherical shell with mass and damping imperfections and parametrically driven by discrete electrodes[J]. Gyroscopy and Navigation, 2011, 2(1): 27-33.

[14] 伊国兴, 谢阳光, 王常虹, 等. 加速度对半球谐振陀螺振动检测系统影响分析[J]. 中国惯性技术学报, 2013, 21(5): 676-681.

YI G X, XIE Y G, WANG C H, et al. Analysis of acceleration influence on HRG vibration detection system[J]. Journal of Chinese Inertial Technology, 2013, 21(5): 676-681 (in Chinese).

[15] FREITAG S, BEER M, GRAF W, et al. Lifetime prediction using accelerated test data and neural networks[J]. Computers & Structures, 2009, 87(19-20): 1187-1194.

[16] WANG X, WU W Q, FANG Z, et al. Temperature drift compensation for hemispherical resonator gyro based on natural frequency[J]. Sensors, 2012, 12(5): 6434-6446.

[17] SONG J W, SONG H M, LEE Y J, et al. Design of oscillation control loop with coarse-precision mode transition for solid-state resonant gyroscope[J]. IEEE Sensors Journal, 2016, 16(6): 1730-1742.

[18] WANG X, WU W Q, LUO B, et al. Force to rebalance control of HRG and suppression of its errors on the basis of FPGA[J]. Sensors, 2011, 11(12): 11761-11773.

[19] ZHURAVLEV V P. Hemispherical resonator gyro withmdata electrodes andncontrol electrodes[J]. Mechanics, 2015, 50(4): 375-378.

[20] 徐芝纶. 弹性力学下册[M]. 5版. 北京: 高等教育出版社, 2016: 100-200.

XU Z L. Elasticity[M]. 5th ed. Beijing: Higher Education Press, 2016: 100-200 (in Chinese).

[21] 赵洪波, 任顺清, 李巍. 半球谐振子动力学方程的建立及固有频率的计算[J]. 哈尔滨工业大学学报, 2010, 42(11): 1702-1706.

ZHAO H B, REN S Q, LI W. Establishment of dynamics equation of HRG resonator and calculation of natural frequency[J]. Journal of Harbin Institute of Technology, 2010, 42(11): 1702-1706 (in Chinese).

[22] 谢阳光. 基于半球谐振陀螺的姿态测量系统研究[D]. 哈尔滨: 哈尔滨工业大学, 2013: 13-36.

XIE Y G. Research on attitude measurement systems based on hemispherical resonator gyro[D]. Harbin: Harbin Institute of Technology, 2013: 13-36 (in Chinese).

[23] BA 马特维耶夫, H И 利帕特尼科夫, AB 阿廖欣, 等. 固体波动陀螺[M]. 北京: 国防工业出版社, 2009: 1-43.

MATVEEV V A, BASARAB M A, ALEKIN A V, et al. Solid state wave gyro[M]. Beijing: National Defense Industry Press, 2009: 1-43 (in Chinese).