小曲率半径医学图像快速三维重构算法研究

王 静

(长春理工大学光电信息学院,吉林 长春 130012)

0 引 言

在70年代后，许多医学成像技术如核磁共振成像、计算机断层扫描、超声波等技术的发展越来越先进，医学上对于人体器官的发展[1]。但是随之而来的还有人们日益增高的医疗需求以及对医学技术的期望。目前大部分的医学图像处理还是停留在二维截面的信息表达，通过简单的坐标叠加，完成医学图像的重构。这个过程虽然简单，但是精确度却远远达不到理想状态。对于三维医疗图像则无能为力，而在医生诊断病人过程中，免不了对其内部器官三维图像进行分析，而传统技术无法对三维医学图像进行有效处理及重构，这会造成病人的病变定位的不准确，耽误病人治疗。为了进一步满足人们医疗需求，提高疾病治疗精度，提出医学图像三维重建技术[2]。

随着各界相关人士的逐渐重视，对医学图像的重构问题研究随之更加深入[3-4]。针对传统方法的不足展开深入分析。对图像的可视化处理在计算机科学领域得到了飞速发展，相关研究逐步向国际拓展。就目前而言，为了更好解决医疗图像的重构问题，需要对图像的三维处理方法进行研究及改进，三维图像重构方法大体上可以分为两类[3]，面绘制重构方法和体绘制重构方法。三维图像的立体性，决定了其特殊性，如果利用面绘制方法来进行重构，则需要将三维图像进行面的切分，这个过程不仅过于繁琐，而且其重构精度远远达不到理想效果。而体绘制重构方法需要大量的立体参数进行计算，运算量大，不适合实际应用。

提出了一种医学图像曲面混乱区域配准方法，对小曲率半径图像三维坐标空间变换参数进行改进，采将坐标误差可接受程度收敛至最优值附近。后期需要分别对融医学三维图像的曲面进行小波分解及小波逆变换，重构得到高清晰医学图像三维曲面。为了验证所提方法的有效性，进行一次实验，并对实验结果进行记录分析。由实验结果表明，所提方法能够高效的对医学图像进行重建，重建效果理想，且速度快，具有很强的有效性。

1 医学图像三维坐标获取的改进

1.1 小曲率医学图像坐标重构中的毛刺问题分析

对小区率头像的毛刺分析，首先应清楚其原理，在图像中首先确定CCD和光源侧所有点的坐标，这是后续问题分析的基础，利用符号窗口匹配理论推测出同一像素在CCD侧和光源侧的位置，构建空间方程，从而获取小区率图像像素的空间坐标。综上所述即是结构光检测系统测距原理[5]，如图1所示。

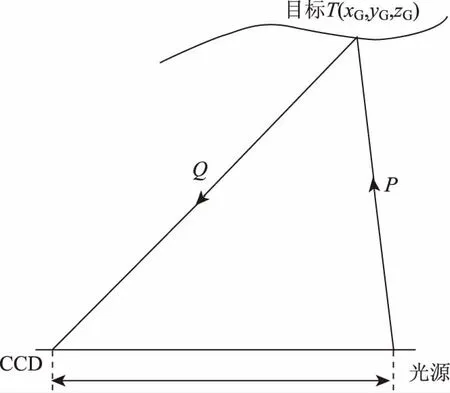
图1 结构光检测系统测距原理图

则光线p的外空间方程为：

(1)

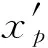
(2)

对CCD侧的接收到的光线Q，可得：

(3)

假设，在发射侧发射出的光线P被CCD所接收，则说明P、CCD交于一点T，则可计算点T在三维全局坐标系下的坐标(xG,yG,zG)。有：

(4)

即：

(5)

两两方程组合求解后，得到Rq、Rq均值，得方程(5)，减少误差。方程(5)中(1)(2)求解，得：

(6)

方程(5)中(1)(3)求解，得：

(7)

方程(5)中(2)(3)求解，得：

(8)

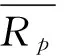
(9)

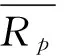
(10)

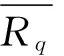
(11)

由上述步骤得到了整体坐标，从理论上分析公式(10)和公式(11)等到的数据应该是相同的，但由于实际测量中难免出现误差，这就造成了结果不等的情况，此时将得到的数据去平均值，作为医学图像特征像素点T的三维全局坐标(xG,yG,zG)。

(12)

为了保证医学图像重构的精确性，对外空间光线方程方法下图像重构效果进行评估[6]，将Z的值设定为1630 mm，对实际平面图进行重构，结果如图2所示。

图2 Z=1630 mm平面重构结果

从图2中可以看出，该重构结果能够表示目标医学平面的大致轮廓，但如果对精度要求较高的情况下则无法得到满意的结论，从图中可以明显看出，该图中含有很多毛刺，从整体重构图来看，毛刺严重程度不等，这说明了这个方法虽然从原理上看可行，但是在实际应用中精度偏低，不具有很好的实用性。这主要是因为小曲率医学图像存在特殊性，图像中有很多坐标是重叠状态[7-8]，当坐标发生多次重叠的情况下，就会形成上图中的毛刺，所以对医学平面图像进行重构即是需要改进三维数据的获取过程。

1.2 医学图像三维重构坐标获取算法改进

由图2可观察重构后的毛刺位置，分析三维坐标后，构建光线方程，若使结果最为准确，要求其中光线方程2和3中Δxq，Δyq，ΔxP，ΔyP均不能为零。通过两两方程组合求解的方式，可以得到三维坐标最终的平均值结果，但该结果并不完全准确，因为在实际处理中并没有考虑光线方程2和3中的参数取值问题。由此得出光源侧所发出的各条光线之间，必定存在某些光线在标定前后的全局坐标未改变或改变甚小[9]，即ΔxP，ΔyP参数值为零或很小；同理可知，在CCD侧接收到的各条光线之间，同样必定存在前后两次标定的成像点坐标改变很小或未改变，即Δxq，Δyq参数值很小或为零。其可能原因可以由公式2、3及公式9、12得知，及Δxq，Δyq，ΔxP，ΔyP这四个参数的取值直接影响着Rp和Rq的值，而不够准确的Rp和Rq值则会导致目标点的错误三维信息，由此导致经过重构后，产生毛刺[10]。为此，提出对该种算法的优化改进处理，即求解公式5的过程中考虑这四个不同参数的取值大小。

首先，比较四个不同参数值的大小，在最小值为Δxq或ΔxP的情况下，利用公式(5)中的2和3方程对Rp、Rq两个参数变量进行求解：

(13)

在Δyq或ΔyP为参数中最小值的情况下，在公式(5)中只利用(1)(3)方程对Rp、Rq两个参数变量进行求解：

(14)

对各参数进行改进优化处理后，得到对应的像素点三维坐标：

(15)

在Matlab环境下进行简单的滤波和插值处理。平面及曲面重的实验工作场景如图3a、b所示，平面与曲面的重建实验结果如图3c、d所示。比较图2可知，经过简单重建处理后，已经修复了大毛刺部分，同时改善了其他部分的小毛刺，修复重建后具有较好的平面效果。

根据传统的标定方法[11-12]，要求标定的设备精度不高，需要手动调整测距和标定的平台，限制了三维检测精度。其三维检测过程中存在较大的实验误差。传统的解码方法对光照等因素的要求过高，而光照这个可变影响因素是无法完全避免的，这就要求首先对三维图像进行关键点的检测，该过程会大幅度降低图像的分辨率，从而影响了三维检测精度。在景深范围内，检测标准平面后，计算得出其相对误差约为0.73%，绝对误差约为11.87 mm。

图3 毛刺消除效果分析

2 医学图像融合方法的实现

目前，存在大部分融合算法所构建的医学图像技术是二维小波变换技术[13]，选取两幅医学图像作为研究对象，融合算法大致流程如图4所示。医学图像融合算法具有差异性，这是因为图像融合原理是通过三维曲面信号小波变换得到数据，再完成融合步骤。

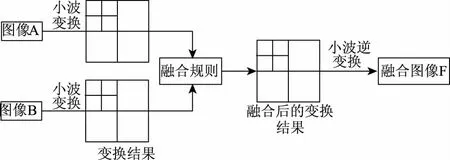
图4 基于小波变换的图像融合过程

在小波变换下，本文所做的图像融合具体步骤[14]为：

(1)首先对需要融合处理的医学图像完成图像配准和图像滤波；

(2)利用小波分解对预处理之后的医学图像进行同和处理，获得源图像高频分量和低频分量；

(3)通过多种运算规则处理高低频系数，将得到的医学图像在各自区域融合处理；

(4)利用小波逆变换技术对上诉过程获得得的高频分量和低频分量进行融合，得到最终需要的融合图像。

通过对上诉融合过程研究总结，得出三维曲面信号条件下的小波变换技术所得医学图像的融合计算公式为：

I(x,y,z)=ω-1(Φ(ω(I1(x,y,z),ω(I2(x,y,z)))))=

ω-1(Φ(W1(x,y,z),W2(x,y,z)))

(16)

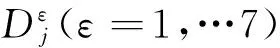
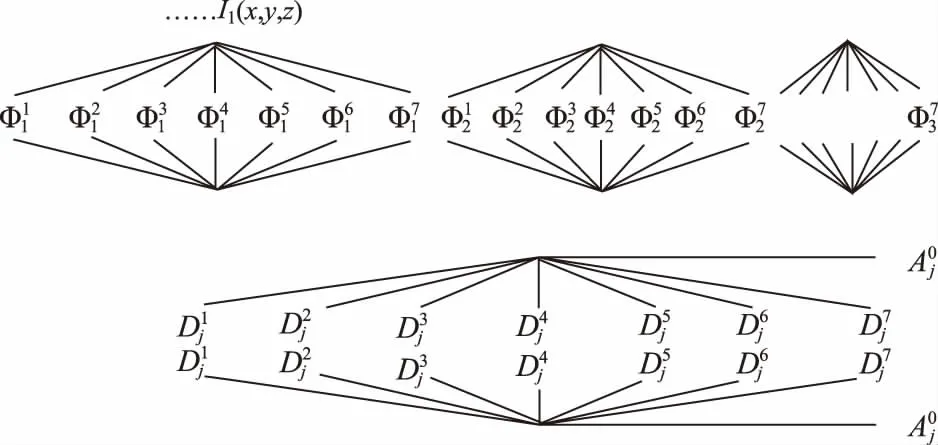
图5 小波分解后各通道融合过程图

二维小波变换和三维下小曲率小波变换下的图像融合算法极为相似，能够通过选择多种Φ算法[16-17]完成多个三维环境下的通过小波变换技术得出的图像具体融合算法。利用随机选取的方法选择两幅图像作为研究对象，选择几个常见的二维小波变换技术转换为三维小波变化技术再进行图像融合，发现得到的算法相似。

(1) 最大值融合

(17)

(2) 去噪融合

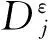
(18)

(3) 高低频融合

将图像高频数据和低频数据全部当作融合图像数据，得出以下公式：

(19)

因为融合后的图像数据仅仅和跟源图像相关，所以三维曲面融合技术的性能研究就能够通过二维图像融合技术性能研究方法进行讨论，比如峰值信噪比(PSNR)法、交叉熵值法、熵值法、均方根误差(RMSE)法和互信息量(MI)法等。

(4) 加权平均融合

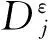
(20)

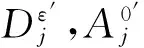
加权平均融合技术是相对比较有优势的技术，其优点[20]是计算过程简单，呈现形式直观，适用于实时处理要求下的图像融合。若要求多幅图像同时进行融合处理时，能够显著提升图像信噪比。但该方法也存在一定弊端，加权平均融合技术的实践原理是对所研究图像的像素完成平滑处理，这种操作会伴随着图像边缘变得模糊。

3 实验结果与分析

3.1 曲面融合试验结果分析

根据上述实验结果能够得出，不同曲面之间做融合处理过程中，不良的拼缝现象仍然有所产生。然而，如果想要达到无缝拼接的目的，就必需要采用融合处理方法对配准后的曲面处理，而本文所提出的是最大值融合的处理办法，用来确定是否为最佳的融合位置的确定方法是利用计算两曲面之间存在的互相关。证明两曲面达到了最优的融合效果时，此时其两曲面之间的互相关为最大值。其中第一部分两融合曲面的归一化互相关，如图6所示。根据图6得出，能够描述两曲面之间为最相关的时候是图中归一化取得到的最大值的地方。从Matlab中能够看出，两融合曲面之间的互相关为最大值时，也就是归一化Max_c=0.44184为峰值时，这时两个曲面之间才达到了最佳的融合效果。

图6 两融合曲面的归一化互相关

在Matlab中，对实验的数据分别进行对应的滤波和插值的处理过程，由此得出三维曲面的拼接融合结果，如下述图7所示。从图7中能够得出，经过修正以后的拼接曲面效果同配准后的曲面融合对比，图像经过修正后配准出现的拼缝毛刺等不良现象也有了明显的消除。

图7 曲面融合效果图

图8描述的是第二组融合曲面的归一化互相关。从Matlab中能够看出，两融合曲面之间的互相关为最大值时，也就是归一化Max_c=0.303 86为峰值时，这时两个曲面之间才达到了最佳的融合效果。

图8 两融合曲面的归一化互相关

在Matlab中，对实验的数据分别进行对应的滤波和插值的处理过程，，由此得出三维曲面的拼接融合结果，如下述图9所示。从图9中能够得出，经过修正以后的拼接曲面效果同配准后的曲面效果相比更加平滑，也改善了一些配准后的拼缝毛刺等现象。

图9 曲面融合效果图

根据图7、图9能够得出，在进行了三维曲面融合处理过程以后，无缝拼接的目的仍然没有在真正意义上得到实现，在整个实验过程中误差依然不断出现。误差的产生主要出现在进行三维曲面融合的过程中，采用小波变换的方法在对曲面归一化互相关处理时会造成模糊等不良结果，这些不良结果使误差不断出现在三维曲面的拼接过程中。

3.2 医学图像重构算法实验应用结果与分析

通过运用医学图像重构算法在实验平台下进行了仿真实验。将采用本文算法的实验结果与采用传统的算法的实验结果分析对比。实验所采用的系统为普通PC机构成的集群系统，dicom影像序列数据是本实验规定所采用的数据，针对实验数据的说明如表1所示。本实验所采用的数据为脑部、胸部等扫描影像数据。

表1 数据说明

通过采用传统串行体绘制算法在1号PC机上做相关的测试实验，得到的实验数据为胸部CT数据，图像像素512×512，实验结果采用串行算法测试得到，且三维图像的绘制仅3.10 s即可完成，如图10所示。然而，虽然只有5层的数据量需要进行计算，但是完成计算的整个过程耗时相当的长，然而在现实应用中，一般数据量都是上百层的数据量，而且计算量与数据量的关系成正比例关系，因此，在实际运用当中，计算速度往往达不到对实时性的要求。

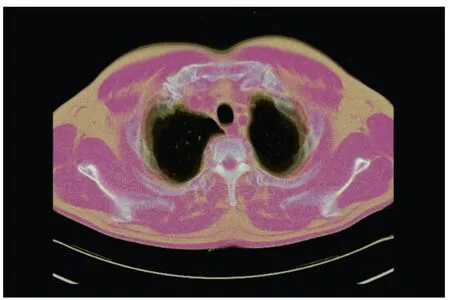
图10 串行算法的胸部数据测试结果

(1)其中第一部分的测试数据为190层脑部CT图像数据。实验最终结果通过多种类型算法测试后得到，如图11所示。由此能够得出，与CPU的图像绘制效果相比，其采用GPU绘制图像的最终效果相对较差。采用1号PC机来对本文的算法进行实验；采用1号、2号和3号PC机来对MPI绘制算法进行实验，设定主节点是1号PC机；采用1号PC机对CUDA的体绘制算法进行实验；采用1号PC机和2号PC机对多机多GPU算法进行实验。四种算法的执行时间，如表2所示。

表2 不同算法的运行时间

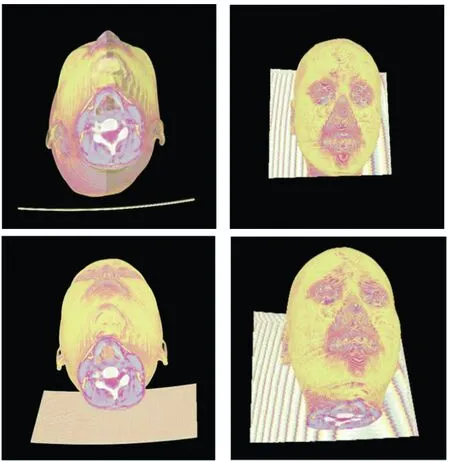
图11 头部数据测试实验结果

在1号PC机上，运用传统串行的图像体绘制算法测试头部200层数据，总耗时大约为132.69 s。分析以上可以得知，虽然1号PC机的计算核心较多(为4个)，该算法虽然结果较为理想，但是过程过于繁琐，算法应用效率较差，无法实现图像绘制书籍的线性增长。这与计算机内部处理也是有关系的，在现代计算机系统中，在对大型数据分析前一般都会有优化处理。虽然传统多核多线程算法会将数据分布到4个不同的核心中计算，但是并不会出现明显的增强4倍处理速度。CUDA的体绘制算法性能较好，这是因为该种算法主要利用CUDA进行大规模的模拟光线计算，具有较好的并行性能。但由于模拟光线的数量过大，CPU所能提供的线程受限，无法对每个射线都进行并行模拟计算。而传统的MPI并行算法中，需要提取一个独立的节点负责任务分配、初始化等工作，只有两个节点可以参与实际计算。由于其中只有一个节点进行初始化等交互性工作，使其计算处理速度较慢，提升效果不高。本文方法中，将计算任务平均分配在不同的各个节点上，由于使用的GPU的处理能力不同，完成任务所用时间也不同，但以最终的任务完成时间作为整体计算时间，因此其计算时间的能力并没有得到有效的线性提升。

(2)利用各种不同算法的处理55层胸部CT数据。实验结果如图12和表3所示。实验发现各种不同的算法虽然在一定程度上加速了体绘制算法，但是并没有达到理论的线性增长速度。因此其增长速度仍需深入探讨研究。

图12 胸部数据测试实验结果

绘制方法串行计算多核多线程基于CUDA算法MPI并行算法本文算法绘制时间25.44s19.63s0.010s15.92s0.009s

4 结 语

医学图像三维重构算法是通过几个不同部分构成的，并且每个组成部分都会决定结果图像重构质量。其中，图像采样、滤波等操作步骤都对直接影响算法的最终结果。因此，几乎很难避免最终图像会出现失真的问题，环状失真是最为常见的一种失真情况，如下面的图13所示，这大大的干扰了图像绘制效果。通过上述的各组实验结果的可以看出图像几乎都出现了失真的问题。那么，下面开始分析造成失真的原因。

(1)采样率：在图像采样理论的基础之上，若图像的采样率比较高，说明与原始数据结构更加接近。互相平行的代理几何体的距离越大，代表采样率越低，失真情况更加恶劣，反之，绘制结果越好。虽然可以通过增加切片层数，进一步的完善采样率，但这样会导致算法的性能大大的降低。结果表明，采样率是直接影响图像失真的一个重要因素。

图13 环状失真

(2)滤波函数：滤波函数能够将离散型数据进行有效变换，使得数据具有连续性，重构的原始信号与一部分离散信号的频谱做积，通过简单整理，然后再将乘积作逆变换，从而得到重构结果。然而用到的三线性插值方法不会对图像结果产生很大的影响，可忽略不计。

(3)分类算法：数据场具有离散性质，所以在光纤不是很理想的情况下，采样点的坐标就会偏离正确位置，因此需要利用插值计算对采样点进行二次调整。因为分类的先后顺序不同，将分类算法分为先分类算法和后分类算法。在此基础上结合传递函数对其继续拧采样处理，因为改函数具有非线性，这就在很大程度上提升了结果的正确率，使得采样频率与理论结果更为接近。传统方法的现实采样精度偏低，存在大量的影响因素，无法满足现实精度要求，因而分类算法极易出现失真的现象。由此可知，分类算法是影响绘制结果的重要因素。

(4)混合精度：采样数据进行混合时，要求采样数据一定是8位精度。采样数据越多，其误差率也会越大，特别是在模糊数据较多的情况下，误差就会更大，这也是出现环状失真的一个重要因素。

实验系统还需要考虑效率问题，其中，最重要的一个指标就是重构速度，它可以直观的衡量可视化算法。算法利用不同的实现方法，其最终的效率也会不同。如果算法在最开始就能将效率问题列入考虑范围之内，就不会对干扰绘制速度。另一方面，需要在系统框架流程的上去看待效率问题，尽可能的降低模块之间的关联度，保持直接调用模式。同时，根据预处理方法对内部流程模块进行优化，该过程可提前预测数据的重复使用情况，以提高图像重构效率。

[1] 张东霞, 甘阳洲, 熊璟,等. 基于口腔计算机断层扫描图像与激光扫描图像融合的牙齿三维模型重构[J]. 生物医学工程学杂志, 2017(1):7-14.

[2] Dong H, Kervran Y, Coulon N, et al. Highly Flexible Microcrystalline Silicon n-Type TFT on PEN Bent to a Curvature Radius of 0.75 mm[J]. IEEE Transactions on Electron Devices, 2015, 62(10):3278-3284.

[3] 周娟. 基于MITK的医学图像三维表面重建算法[J]. 计算机科学, 2016, 43(S1):194-197.

[4] 丰焕亭, 陈春阳. 虚拟医学解剖实验的关键方法仿真[J]. 计算机仿真, 2016, 33(4):411-414.

[5] Hill D E, Hopkins D F. Effect of small radius of curvature on transonic flow in axisymmetric nozzles.[J]. Aiaa Journal, 2015, 4(8):1337-1343.

[6] 范阳阳, 倪倩, 温铁祥,等. Freehand三维超声体数据重建的最新研究进展[J]. 中国生物医学工程学报, 2017, 36(1):92-102.

[7] 罗敏, 李辉. 低照度条件下超分辨率人脸图像采集系统设计与实现[J]. 计算机测量与控制, 2016, 24(11):229-231.

[8] Dong H, Kervran Y, Coulon N, et al. Highly Flexible Microcrystalline Silicon n-Type TFT on PEN Bent to a Curvature Radius of 0.75 mm[J]. IEEE Transactions on Electron Devices, 2015, 62(10):3278-3284.

[9] 任立胜, 王立中. 基于曲率尺度空间的角点检测图像匹配算法分析[J]. 电子技术应用, 2016, 42(12):112-114.

[10] Jie M, Xi H, Fan W. The effects of thermal field on radius of curvature interferometric testing[J]. Optical Review, 2015, 22(2):299-307.

[11] 陈正兵. 基于深度图像的室内三维平面分割方法研究[J]. 电子设计工程, 2016, 24(24):158-160.

[12] 陈思思, 朱德喜, 马庆凯,等. 基于谱域OCT图像的

人眼前节生物学参数自动测量[J]. 中华实验眼科杂志, 2016, 34(4):345-350.

[13] 金显华, 睢丹. 基于拟蒙特卡罗和Taubin平滑的三维图像重构算法[J]. 微电子学与计算机, 2015(8):163-166.

[14] 赵志升, 张晓, 梁俊花,等. 融入背景差分连续重构的心脏医学图像重建[J]. 科技通报, 2015, 31(8):207-209.

[15] 赵龙, 韦群. 序列图像三维重构中点云精简算法的研究与改进[J]. 计算机工程与应用, 2016, 52(8):211-216.

[16] Hoffmann M, Brost A, Koch M, et al. Electrophysiology Catheter Detection and Reconstruction from Two Views in Fluoroscopic Images.[J]. IEEE Transactions on Medical Imaging, 2016, 35(2):567.

[17] 尹阳, 刘君. 重击下颅骨CT图像裂痕区域检测方法研究[J]. 计算机仿真, 2016, 33(12):366-369.

[18] Losada M A, López A, Mateo J. Attenuation and diffusion produced by small-radius curvatures in POFs.[J]. Optics Express, 2016, 24(14):15710.

[19] Ericson E A, Lyzenga D R. Performance of a numerical iterative solution of the surface current integral equation for surfaces containing small radii of curvature[J]. Radio Science, 2016, 33(2):205-217.

[20] 谌湘倩, 马绍惠, 须文波. 基于有序子集加速拆分算法的三维CT图像重建[J]. 现代电子技术, 2016, 39(6):104-107.