基于能量解耦法的轻型载货商用车振动系统模态分析

许恩永

（东风柳州汽车有限公司，广西柳州545005）

乘坐舒适性是客户评价汽车的重要指标之一，在汽车生产销售过程中占有极其重要的位置，目前主要通过座椅处的振动状态来衡量，而汽车动力学是从根本上解决汽车行驶问题过程中遇到诸多振动难题的复杂而又有效的一门学科。目前建立汽车系统动力学方程常用的方法有：拉格朗日法、牛顿—欧拉法和凯恩法等[1]。动力学是汽车进行模态分析的前提，而模态分析是控制振动、抑制噪声等解决NVH常见问题中最为有效的一种分析方法[2]。实际中，容易求得线性振动系统的固有频率和固有振型，却难以判断广义坐标与固有频率之间的对应关系，尤其是广义坐标之间耦合程度较高时，文献[3-5]等都完成了汽车平顺性的建模仿真，但仍没有对固有频率与广义坐标的对应关系进行分析。

本文以某轻型载货商用车为例，通过简化建立该汽车五自由度力学模型，根据牛顿—欧拉法建立其动力学方程，并采用动力总成悬置系统隔振优化的惯用方法——能量解耦法[6-8]，基于常用矩阵化数学软件MATLAB得到该车座椅处最为关注的系统各阶模态与各广义坐标的能量分布，说明不同模态所对应的广义坐标以及各广义坐标的耦合情况，为提高商用车平顺性提供理论依据。最后，利用动力学软件ADAMS建立其动力学模型，并进行模态和振型分析完成上述计算结果进行验证。

1　五自由度振动系统模态分析

1.1　力学模型

商用车是一个极为复杂的刚柔耦合系统，本文研究的某轻型载货商用车模型如图1所示。

图1　某型商用车模型

为建立汽车座椅的五自由度模型分析平顺性相关的模态特性，根据该商用车的结构特点进行适当简化，得到由轮胎、悬架、车身和人椅所组成的刚体系统，其力学模型如图2所示。

图2　汽车五自由度振动系统力学模型

图2可见，该模型具有五个自由度，取广义坐标为（i=1，2，3，4，5），分别表示汽车前簧下质量垂向位移、汽车后簧下质量垂向位移、车身垂向位移、车身俯仰角位移和人椅位移；和表示前后轮的路面不平激励。本文中采用的商用车动力学参数如表1所示。

表1　某型号汽车动力学参数

1.2　动力学方程

汽车五自由度振动系统作平面运动，其动力学分析相对简单，故可采用牛顿第二定律来建立其动力学方程，如下：

建立上面动力学方程需要注意下面两点：

①本文在建立动力学方程时，之所以没有考虑弹性元件的原长和各个部件本身的质量，是因为各个自由度的位移是相对于各自的静平衡位置。

②本文主要进行的是自由振动的响应，即zg1=zg2=0.

1.3　质量、刚度和阻尼矩阵

通过对式（1）至式（5）的合并与化简，可以得到如下的形式：

其中：

1.4　固有频率和振型矩阵

本文主要讨论系统无阻尼自由振动，故令阻尼系数为0，得到：

由振动理论可知，通过对矩阵K和M求广义特征值和广义特征向量，即可得到对角矩阵Λ和振型方所组成的对角矩阵。通过对Λ进行开方即可得到系统各阶圆频率（单位rad/s），再除以2π便可得到系统各阶固有频率（单位Hz）。充分利用矩阵数学软件MATLAB在矩阵计算中的优势，调用其子函数，输入命令[Λ Φ]=eig（K，M），即可得到振型矩阵 Λ 和对角矩阵Φ。

将表1的汽车动力学参数代入式（7），得到质量和刚度矩阵。利用MATLAB软件编制程序，容易得到该系统的振型矩阵Φ和对角矩阵Λ为：

根据对角矩阵及前面介绍的关系可得到系统的前五阶固有频率为：f1=1.31 Hz，f2=2.36 Hz，f3=2.98 Hz f4=10.52 Hz，f5=11.72 Hz.

利用MATLAB软件求解得到的固有频率是按照从小到大的顺序进行排列的，因此难以得知各广义坐标所对应的固有频率。如果单纯地通过观察振型矩阵各列中最大的元素获取贡献量最大的自由度，由于没有考虑到质量、单位和正负号等问题，很多时候并不准确，尤其是在广义坐标的耦合程度较高时容易判断出错。为弥补该不足，下面利用能量法来解决这一问题。

2　汽车五自由度振动系统能量分布

2.1　能量法解耦法

通常振动系统中都存在不同程度的耦合作用，使得系统的激振频带加宽，给隔振和频率配置带来困难，不利于减振降噪。为对这一程度做出评价，通常用某一广义坐标的动能占某阶模态总动能的百分比作为模态解耦的评价指标，即能量法解耦。

根据式（7）即可求得圆频率 ω（i=1，2，3，4，5）及振型矩阵Φ，由此便可求得系统各阶主振动时的能量分布，将它写成矩阵的形式，即为能量分布矩阵。

当系统作i阶主振动时的最大动能为：

展开得：

mkl表示质量矩阵的第k行、第l列元素，（φi）k和（φi）l分别表示振型（φi）的第k、l个元素。

第k个广义坐标在第i阶主振动最大动能所占的百分比为：

如果Tp（k，i）=100%，则意味着第i阶主振型的能量全部集中在第k个广义坐标上，其余广义坐标分配到的能量均为零，即该阶模态对应的主振动没有耦合性，即实现了完全解耦。

根据上面叙述的能量解耦法理论基础，利用MATLAB软件开发能量解耦法函数matrix_of_enegy。该函数的输入参数为振型矩阵Φ、对角矩阵Λ和质量矩阵M，输出参数为能量分布矩阵Tp.函数调用格式如下：

2.2　汽车五自由度振动系统能量分布矩阵

根据前面的能量解耦法函数、对角矩阵、振型矩阵和质量矩阵，得该系统的能量分布如表2所示。

表2　系统的固有频率和能量分布

从表2中可知，第一至第五阶模态分别对应于z4、z3、z5、z2和 z1，它们所占的能量最大，说明了各自由度的所对应的固有频率以及各个自由度的耦合情况；从表中还可以看出，第二和第三阶模态下，z3和z5两自由度的频率接近且耦合程度较高，，而其它另外三阶的解耦率都超过了90%，已经具备很好的解耦效果。

3　汽车五自由度振动系统模态验证

3.1　五自由度振动系统ADAMS模型

多体动力学分析软件ADAMS是进行机械系统动力学仿真分析的权威，在汽车行业应用广泛，故本文利用ADAMS软件建立该五自由度系统的动力学模型，如图3所示，对MATLAB计算结果的验证。为了更好的看出振型，对模型进行简化建立其ADAMS的简化模型，如图4所示。

图3　轻型载货商用车五自由度ADAMS模型

图4　五自由度简化模型

3.2　固有频率对比

通过ADAMS求解器对该模型的系统固有频率进行求解，得到其前五阶固有频率，并将其结果填入表3中，为了与前面MATLAB软件的结果进行对比，将MATLAB的结果也填入表3中。

表3　MATLAB与ADAMS求解系统固有频率对比

从表3中可以看出本文所开发的MATLAB程序求解结果与ADAMS求解结果相差极小，误差在2%左右，由此说明了该五自由度振动系统建模与求解结果是正确且可靠的。

3.3　ADAMS模型固有振型

对本文建立的ADAMS模型进行模态分析，其前五阶振型结果如图5所示。

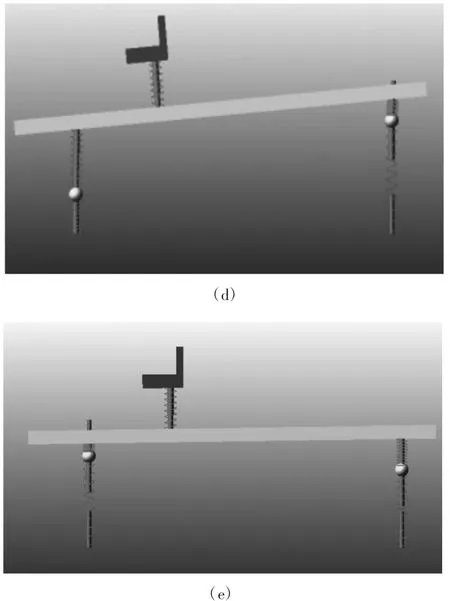
图5　五自由度振动系统ADAMS模型的前五阶振型

从图5可见，第一阶模态的振动主要集中在上；第二、三阶模态的振动主要集中在和上；第四阶模态的振动主要集中在上；第五阶模态的振动主要集中在上。这与表2的能量分布关系是十分吻合的，再次验证了本文模型和计算方法的正确性和可靠性。而影响驾驶员乘坐舒适性的振动频率主要是第二阶模态，振型为座椅的上下振动，改善其舒适性可以此为根据。

4　结束语

本文通过对汽车结构分析和简化，建立五自由度振动系统并进行了模态分析，利用能量解耦法基于MATLAB软件得到了该系统的能量分布矩阵，获得了各广义坐标所对应的固有频率以及各阶模态各广义坐标耦合程度，最后通过ADAMS来验证了结果的正确性，为汽车的隔振与优化，舒适性的改进措施提供理论基础。

参考文献：

[1]刘延柱.高等动力学[M].北京：高等教育出版社，2001：239.

[2]李 伟，史文库.模态分析在轻型载货车变型设计中的应用[J].噪声与振动控制，2008，28（04）：75-78.

[3]朱位宇.某重型卡车平顺性研究及悬架阻尼优化设计[D].长沙：湖南大学，2012.

[4]宋韩韩.基于ADAMS的刚柔耦合整车模型平顺性仿真研究[D].锦州：辽宁工业大学，2015.

[5]钱 凯.汽车行驶平顺性分析及粒子群算法在悬架优化中的应用[D].重庆：重庆交通大学，2013.

[6]王郡成.某中型载货汽车动力悬置系统优化研究及应用[D].青岛：青岛理工大学，2015.

[7]孙永厚，李 峤，刘夫云，等.汽车动力总成悬置系统的解耦优化研究及应用[J].机械设计与制造，2016（9）：147-149.

[8]薛 华，刘志强，刘 岩，等.基于 Matlab的动力总成悬置系统解耦优化[J].噪声与振动控制，2015，35（2）：65-68.