基于立即辐射度的实时全局光照算法
袁璐
(四川大学计算机学院,成都 610065)
0 引言
随着计算机硬件处理能力的不断提升,计算机图形学也迎来了崭新的局面。全局光照模拟作为计算机图形学中活跃的研究方向,在增强图像渲染的真实感上扮演者不可或缺的角色。全局光照的模拟一直以来被广泛的应用在不同的领域,如卡通片绘制、电影制作以及游戏渲染等。然而由于全局光照计算量耗费巨大很难达到实时渲染,因此快速渲染成为了全局光照的重要研究方向之一。
立即辐射度算法作为全局光照算法中的一种,减少了预计算部分,使全局光照实时化成了可能。然而由于为达到真实的渲染效果,目前大部分基于立即辐射度的算法都是离线渲染的。因此为提升渲染效率,本文立将即辐射度算法应用到GPU上,同时通过Lightcuts算法进行进一步的加速计算。
1 相关工作
Keller在1997年提出立即辐射度算法,该算法的核心思想是利用光照辐射度的特性,在场景中被直接光照照亮的地方生成二次光源,即虚拟点光源。并用这些虚拟点光源进行直接光照计算,从而代替复杂光照计算,模拟出真实的全局光照效果。虽然该算法的提出让全局光照的研究方向有了很大发展,但该算法即使在对仅有402个面片的场景进行渲染时,也需要花费24秒的时间。
因此Walter等人于2005年在立即辐射度算法基础上提出的Lightcuts算法,通过对场景中生成的虚拟点光源进行聚类,并用二叉树将相似的光源进行合并以减少场景中虚拟点光源的数量,渲染效率有了很大的提升。
2 算法概述
本文通过用OpenGL渲染管线计算立即辐射度算法中光线跟踪和虚拟点光源生成的过程,再结合Lightcuts算法减少虚拟点光源的数量,最后通过延迟着色(deferred shading)进一步加速光照计算。
2.1 立即辐射度算法
立即辐射度算法计算主要分为两部分:虚拟点光源创建和光照计算。
在虚拟点光源创建部分,首先对场景中的原始光源随机选取方向生成初始光线,再跟踪初始光线并判断光线是否与场景有交点,若有交点则在得到的交点上创建虚拟点光源。虚拟点光源的位置信息和法线信息与得到的交点相同。与基于物理的方法不同,为提升渲染效率,本文中虚拟点光源的贡献度不通过贡献度计算公式计算,而是直接将交点处的漫反射材质属性作为虚拟点光源的贡献度。同时本文只考虑一次间接光照,即虚拟点光源只生成一次,只考虑原始光源生成的初始光线与场景相交,不考虑虚拟点光源再次生成光线与场景相交。
在虚拟点光源间接光照计算部分,对每个着色点计算每个光源对其光照贡献度,并将光照贡献度进行累加,作为着色点最后的光照值。
2.2 Lightcut算法
Lightcuts算法提高场景渲染速率的本质是对场景中光源的数量进行简化。通常来说,场景中的光源数量减少由此会导致渲染结果严重失真。然而由于人眼察觉变化的能力有限,所以只需把减弱后的光源亮度控制在人眼不能察觉的范围内,就可达到减少光源数目而渲染结果亦不失真的目的。根据韦伯定律,在最坏的情况下,人眼能够察觉的亮度的变化通常仅仅在原始亮度的1%之下。但通过实验表明,将误差阈值控制在2%也能得到较好的渲染结果。算法实现步骤如下。
(1)构建光源树
光源树是一棵二叉树,叶节点为原始虚拟点光源,内部节点为代表性光源。光源树的构建需要比较两个光源的相似度,相似度的计算如公式(1)所示:

对于点光源常量c恒为0,公式(1)可变为:

其中Ic为两个光源的亮度之和,αc表示两个光源轴对齐包围盒的对角线长度。权值W越小,则两个光源的相似度越高。
根据公式(2)光源树构造的具体步骤为:
1)选取原始光源中的一个光源作为起始光源a,遍历剩余光源,查找与光源a相似度最高,即公式中W最小的光源b。
2)为光源a与光源b构建父节点,在两个光源之中随机选取一个光源作为代表性光源。对于光源a,有Ia/(Ia+Ib)的概率被选中为代表性光源。
3)将代表性光源加入光源集合中,并在光源集合中删除光源a和光源b。
4)重复步骤1-3,直至光源集合中只剩一个光源,即所建光源树的根节点,至此建树完成。
(2)计算光照估算值及其上界
Walter等给出的每个像素上光照贡献度计算公式为(3)所示:
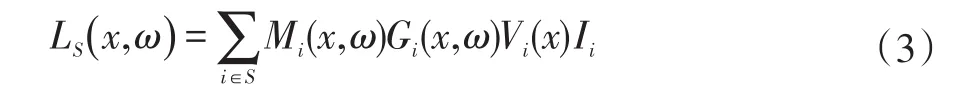
其中,S为所有原始虚拟点光源的点集,i为其中一个光源,x为像素上一点,ω为视点方向,M为光源i的材质因子,G为光源i的几何因子,V代表光源i的可见性,I表示光源i的亮度。
为简化运算,可用光源树上代表性光源k的材质项、几何项、可见项来近似代替所有叶节点原始光源。则公式(3)变换为:
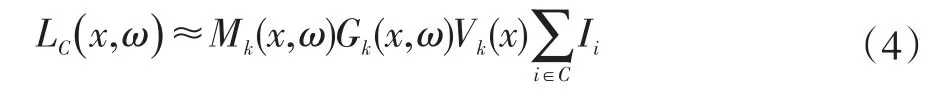
其中,C为一簇光源点集,C⊆S,k为代表性光源。
Walter给出估算LC(x,ω )上界的方法,如公式(5)所示:
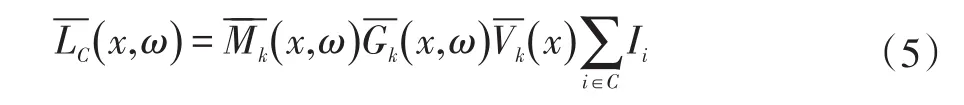
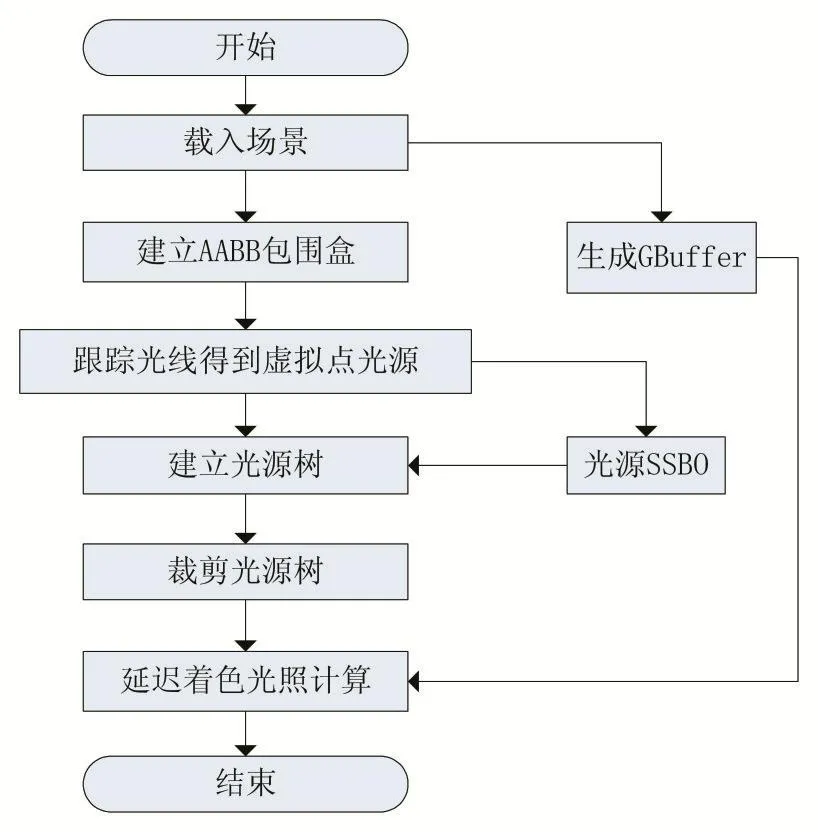
图1
(3)裁剪光源树
光源树裁剪的最终目的是得到一系列可代替原始光源的光源节点的集合,即一条光源割(lightcut)。由韦伯定律,人眼能感知的亮度变化为原始亮度的1%,而Walter等用实验证明原始亮度的2%作为误差阈值就能得到很好的渲染结果。因此上界与估算值的误差只要小于原始光源亮度估算值的2%,则估算值便可作为精确值的近似,并且可认为是人眼不易察觉的误差。
依据韦伯定律,光源树的裁剪过程如下:
1)对于每个像素点,从光源树的根节点开始,将根节点压入备选池中,并计算其上界值Lˉ()x,ω 与估算值L(x,ω)。
最后剩余在备选池中的点即为对应像素点的一条光源割。对于每个像素点都有一条光源割,在渲染时用这条光源割上的光源取代原始光源进行计算。
2.3 实现流程
本文虚拟点光源的生成和光照计算都是在GPU上实现的。为了存储在计算着色器(Compute Shader)中计算得到的虚拟点光源,同时在CPU与GPU中进行数据传递,在OpenGL4.3版本的支持下,本文采用着色器存储缓冲区对象(Shader Storage Buffer Object,SSBO)作为光源的存储结构。为增加物体的层次感和深度感,本文对每个光源都做了一次阴影映射(Shadow Mapping)以产生直接阴影和间接阴影。
本文算法主要流程如图1所示。
首先在CPU端将场景和原始光源载入,同时对场景建立坐标轴对称包围盒(Axis-Aligned Bounding Box,AABB),该包围盒用作后续的光线求交。
然后在GPU端对场景先渲染一次,获得场景的位置、法线和颜色信息,并存在叫做G缓冲(G-Buffer)的纹理中。
再对原始光源随机选取N个方向,作为初始光线。跟踪光线,判断光线与场景包围盒是否有交,若光线与场景包围盒有交点,则生成一个虚拟点光源,且将交点处的位置、法线和漫反射纹理信息赋值给该虚拟点光源,然后把该虚拟点光源存入SSBO中。
接着在CPU端对得到的虚拟点光源根据公式建立光源二叉树,将该光源二叉树转换成二维数组,存入一张纹理中传入GPU端。
最后结合第一遍渲染管线得到的场景几何信息,为每个片元选择合适的光源割,将光源割用作延迟着色光照计算。
3 实验及分析
本文实验采用配置为Intel Core i3 4160的CPU,NVIDIA GeForce GTX 960的显卡,DDR3 8G的内存。在1个初始光源的康奈尔盒中,产生100个VPL的渲染效果如图2所示。

图2
本文在相同的硬件环境和场景下,对使用了Lightcuts算法和未使用Lightcuts算法的进行了对比。实验场景中初始光源为1个,未使用Lightcuts产生了400个虚拟点光源,帧率为34fps。而使用Lightcuts裁剪后虚拟点光源数量变为182个,帧率为59fps,渲染效果对比如图3所示。
4 结语
立即辐射度算法是一种不需要预处理的近似全局光照算法,通过在直接光照照射点上产生虚拟点光源,进而模拟出间接光照的效果。因此特别适合用作实时全局光照计算。由于目前大部分基于立即辐射度的算法都是非实时渲染,因此本文基于GPU渲染管线的支持,提出了一种实时的立即辐射度实现的方法,并得到较好的渲染效果。
同时本文对走样现象未作处理,且未考虑复杂场景,不能满足大型动态场景的实时渲染。另外本文实验场景都是基于漫反射材质,因此丧失了镜面材质等的全局光照效果。以上缺陷都是本文接下来的研究重点。
参考文献:
[1]Kajiya J T.The Rendering Equation[J].Acm Siggraph Computer Graphics,1986,20(4):143-150.
[2]Keller A.Instant radiosity[C].Proceedings of the 24th Annual Conference on Computer Graphics and Interactive Techniques.1997:49-56.
[3]Segovia B,Iehl J C,Péroche B.Metropolis Instant Radiosity[J].Computer Graphics Forum,2007,26(3):425–434.
[4]Laine S,Saransaari H,Kontkanen J,et al.Incremental Instant Radiosity for Real-Time Indirect Illumination[C].Eurographics Symposium on Rendering Techniques,Grenoble,France.DBLP,2008:277-286.
[5]Dong Z,Grosch T,Ritschel T,et al.Real-time Indirect Illumination with Clustered Visibility[J].Proc Vision Modeling&Visualization,2009.
[6]Walter B,Fernandez S,Arbree A,et al.Lightcuts:A Scalable Approach to Illumination.ACM Transactions on Graphics,2005,24(3):1098-1107.
[7]Walter B,Arbree A,Bala K,et al.Multidimensional lightcuts[C].ACM SIGGRAPH.ACM,2006:1081-1088.
[8]Walter B,Khungurn P,Bala K.Bidirectional lightcuts[J].ACM Transactions on Graphics,2012,31(4):1-11.

