基于Minimum s-t Cut三维表面重建算法

詹洋，尹颜朋

（四川大学计算机学院，成都 610065）

0　引言

随着计算机视觉技术发展，3D点云获取更加便捷。然而如何根据3D点云重建出完整而准确的三维表面仍然是一个难题。本文的主要目的是采用多视图三维重建算法所产生的3D点云作为输入，重建出尽可能完整而准确的表面模型，为VR（Virtual Reality），AR（Augmented Reality）等提供三维模型。常见的多视图三维重建算法有 Structure-from-Motion（SfM）[1]、planesweeping[2]、growing based[3]等。本文采用 Bundle Adjustmen[4]三维重建算法获取稀疏点云，PMVS[5]对稀疏点云进行优化和加密，得到稠密3D点云。目前常用的三维表面重建的算法有：泊松（Poisson）表面重建[6]，泊松表面重建采用隐函数的方式拟合3D点云，从而得到水密的三维表面模型，但缺点是易受噪声的干扰而丢失细节信息；Calakli F 等提出 SSD（Smooth Signed Distance）表面重建[7]，采用变分的方法计算三维表面模型，其缺点也易受噪声的干扰；Laurentini提出一种Visual-hull[8]的方法，但对实验条件要求苛刻，无法适应室外的情况。其中泊松表面重建和SSD只运用到三维点的坐标信息，而忽略其他例如可见性等信息，Visual-hull虽然利用可见性信息，但其无法适应室外条件。可见性为每个三维点由哪些摄像机产生，即可见性序列。通过可见性信息，可以去除大量噪声和重现三维表面细节。本文采用Delaunay三角化对3D点云空间进行分解，利用可见性信息将表面重建问题转化为能量最小化问题，构建有向图，采用Minimum s-t Cut进行优化得到三维表面重建模型。图1为本文算法和泊松表面重建算法、SSD（Smooth Signed Distance）表面重建算法，通过对比可以看出本文算法可以去除噪声的干扰且呈现细节信息。

1　背景

1.1　Delaunay三角化

对任意在d维空间中的点集进行三角化网格操作，其原理是将其凸包分割为单形。Delaunay三角化具有空球属性，简单来说，在每个单形外接球中不存在d+2个点，所以Delaunay三角化是唯一的。在计算机图形学和表面处理中Delaunay三角化是一个常用的工具。

图1　

1.2　Minimum s-t Cut

有限元有向图G(V,E)，其中V={v1,v2,…,vn}为顶点，E为有向边其非负权重为wpq。额外增加两个特殊顶点，源点s和终点t。运用s-t Cut算法可以将顶点V分为两个集合 S和T，其中 s∈S,t∈T。其能量方程为：

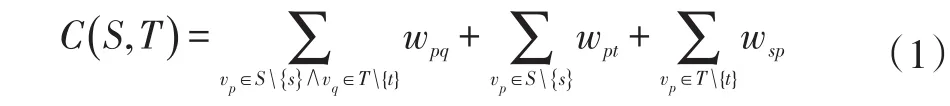
其中wpt为顶点p到终点t构成的有向边的权重，wsp为源点s到顶点p构成的有向边的权重，wpq由顶点p到顶点q构成的有向边的权重。应用Ford-Fulkerso[9]理论可将s-t Cut转化为最大流最小割求解，使得C()S,T的能量最小。

2　重建算法

通过Bundle Adjustmen加PMVS得到稠密3D点云以及每个点的可见性序列。第一步是对3D点云P进行Delaunay三角化自适应的四面体分解。由于3D点云中可能存在噪声点，为了减弱噪声的影响，在Delaunay三角化过程中，对当前插入的三维点(p,C)∈P,其中p为三维坐标，C为可见性序列集合。先检查是否已经插入，如果已经插入只需找到插入点更新其可见序列信息，如果没有，则查找其最近邻并根据当前点的可见性序列将当前点和其最近邻投影到二维空间中，检查其像素差，如果其像素差小于k则当前点不插入只更新最近邻点可见序列信息，否则插入当前点。

得到Delaunay三角化T结果后，下一步需要利用可见性信息将表面重建问题转化为能量最小化问题，其能量方程的形式为：

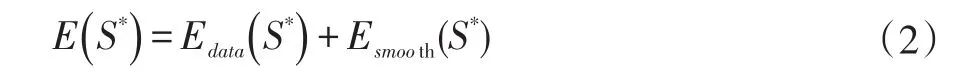
其中S*为目标表面。Edata是数据项,Esmooth为平滑项。Edata记录Delaunay三角化中每个三角形的权重，也是有向图中有向边的权重。其公式为：

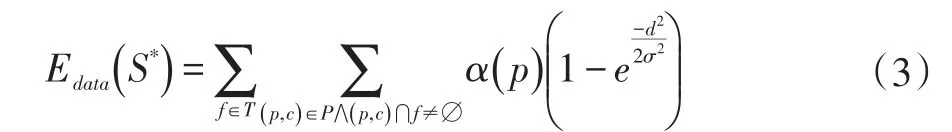
其中 f为Delaunay三角化T中三角形，()p,c为3D点云P包含可见性序列中摄像机点坐标（c∈C）-三维点（p）坐标点对，C为可见性序列集合，α(p)为当前点p与三角形 f交点的个数，d为交点距p的距离，σ为调节参数。其计算的原理是，对于每个三维点(p,C)∈P,，每个摄像机点坐标（c∈C）-三维点（p）坐标点对，计算线段seg（c,p）与Delaunay三角化 T所有相交的面，并计算交点距p的距离d,包含c的Delaunay四面体标记为outside并于源点s相连构成有向边，包含p的Delaunay四面体标记为inside并与终点t相连构成有向边，为了减弱噪声影响，采用距p点很小距离σ作为线段的终点。具体形式见图2（a）。上述计算原理可以归结为线面交的问题，如果用完全遍历的方式其时间复杂度为Ο(npncnf)，其中np为三维点的总数，np为摄像机的个数，nf为Delaunay三角化中三角形的个数，时间复杂度大。而线面交的问题可以转化为碰撞检测问题，可以采用AABB tree来减少时间复杂度，其时间复杂度可以减少为Ο(npnclognf)，可以很好地提高效率。

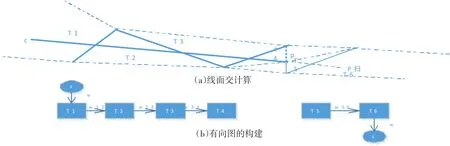
图2　

图3　

如果只有Edata项重建表面S*易受到尖锐三角形的干扰，产生不平滑的表面。所以Esmooth来去除S*中尖锐的三角形，使得目标表面平滑。其目标是尽可能地得到正三角形。实现方法为，在Delaunay三角化 T中所有的三角形对应两个四面体，分别计算四面体外接球与三角形所在的平面形成的夹角的余弦值，当余弦值越大，说明三角形的质量越好，其公式为：

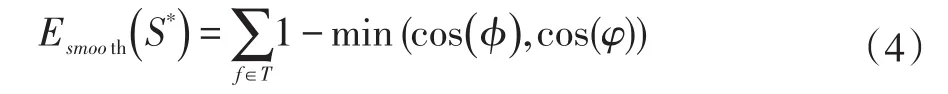
其中 f为Delaunay三角化T中三角形，ϕ、φ为f对应平面与四面体外接球形成的夹角。

分别计算出Edata，Esmooth后，就可以得到每个有向边的权重，将Delaunay三角化中每个四面体当作有向图的顶点，每个三角形当作有向图的有向边，按照图2（b）的方式构建有向图，通过运用Minimum s-t Cut算法进行优化，对Delaunay三角化中每个四面体进行标签分配（inside or outside），其中不同标签两个相邻四面体之间的三角形，即割边就是我们所求的目标表面S*。

3　实验结果

采用开源数据集对重建算法进行验证，OWL有30张分辨率为5184×3456图像，hall有61张3008×2000图像。通过图1说明可以得到本文算法可以去除大量噪声点的影响且重建出表面细节，而poisson表面重建和SSD表面重建算法易受噪声点的影响。图3实验说明本问算法可以较好地呈现出表面的细节，例外地面，门户等。实验结果表明利用可见性信息结合用Minimum s-t Cut的方式对三维点云进行表面重建可以有效地减少噪声对目标表面的干扰而可以重建出精细的细节，能够较准确而完整地重建出三维表面模型。

4　结语

本文采用Delaunay三角化方式对3D点云空间进行自适应分解，利用可见性信息将表面重建问题转化为能量最小化问题，构建有向图，以Minimum s-t Cut方式求解能量最小化问题，得到最终表面重建模型。实验表明基于Minimum s-t Cut三维表面重建算法可以重建出较完整且准确的三维表面模型，具有一定的研究价值。但本文算法还需在效率上进行完善，需要继续改进。

参考文献：

[1]R.Hartley and A.Zisserman,Multiple View Geometry in Computer Vision[M].Cambridge University Press,2003.

[2]R.Collins.A space-Sweep Approach to True Multi-Image Matching[J].Technical Report UM-CS-1995-101,1995.

[3]Y.Furukawa and J.Ponce.Accurate,Dense,and Robust Multiview Stereopsis[J].In CVPR,2007.

[4]Agarwal S,Snavely N,Seitz S M,et al.Bundle Adjustment in the Large[C].European Conference on Computer Vision.Springer,Berlin,Heidelberg,2010.

[5]Furukawa Y,Ponce J.Accurate,Dense,and Robust Multiview Stereopsis[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2010,32（8）:1362-1376.

[6]Kazhdan M,Hoppe H.Screened Poisson Surface Reconstruction[J].ACM Transactions on Graphics（TOG）,2013,32（3）:29.

[7]Calakli F,Taubin G.SSD-C:Smooth Signed Distance Colored Surface Reconstruction[M].Expanding the Frontiers of Visual Analytics and Visualization.Springer London,2012:323-338.

[8]A.Laurentini.The Visual Hull Concept for Silhouette-Based Image Understanding.PAMI,16（2）:150-162,February 1994.

[9]Ford Jr L R,Fulkerson D R.Flows in Networks[M].Princeton University Press,2015.