基于相空间重构ARIMA和SVR的母线净负荷预测

金山红，朱 想，赫卫国，王 波，梅 飞，李玉杰，袁晓玲，刘皓明

（1.国网浙江省电力公司 嘉兴供电公司，浙江 嘉兴 314000；

2.中国电力科学研究院，南京 210003；3.国网浙江省电力公司 宁波电力公司，浙江 宁波 315000；4.河海大学 能源与电气学院，南京 211100）

电力系统需要向用户提供安全、可靠的电能，由于电能本身不能大量存储的特点，实时的供电和负荷平衡是电力系统稳定运行的关键因素之一，负荷预测则是保证这种平衡的一个重要手段。随着新能源技术的不断发展，风电、光伏等分布式电源并入电网，其强烈的随机性及波动性将进一步对电网的稳定运行造成威胁，所以准确的母线净负荷预测对电网的安全、经济运行具有重要意义。母线净负荷受到作息时间、生产工艺、气候、节假日及其他突发事件等的影响，具有时间性和随机性等特点，难于精确建模和预测［1］。

迄今为止，国内外专家学者在净负荷预测的理论和方法方面已经取得了卓有成效的研究成果。净负荷预测方法主要分为经典预测方法和现代预测方法。经典预测方法主要包括时间序列预测法及回归预测法，通过对净负荷历史的观测数据进行统计分析，建立数学模型，从而实现对未来净负荷的预测。由于电力系统负荷的随机性和很强的非线性，经典方法的应用往往存在一定局限性，现代预测方法的研究为负荷预测提供了强有力的工具。目前较多使用的主要包括神经网络、模糊逻辑、灰色理论和小波分析等。

文献［2］采用相似日的负荷预测技术，将历史数据以一周为周期进行分组选取与预测日相似的负荷情况进行预测。文献［3］—文献［5］将支持向量机与聚类分析和经验模态等算法相结合，提出了综合性的净负荷预测方法。文献［6］—文献［9］首先采取最优交集、并行化等对样本数据进行优化，在保证预测精度的基础上减少了工作量。文献［10］—文献［11］考虑了电力系统负荷自身的变化特点及分布式电源接入的影响建立综合的净负荷预测模型。文献［12］对比了叠加性和综合性2种净负荷预测的方法，提出了一种综合的净负荷预测方法。文献［13］提出了基于小波变换和层次聚类分析的配变短期负荷预测方法，通过数据分析，验证了提出方案对所研究案例的适用性。文献［14］提出了一种兼容需求侧资源的负荷预测新方法，通过多层次叠加技术测算到预测区域内考虑需求侧资源的最大负荷，在此基础上构建考虑需求侧资源的负荷预测模型。

随着分布式电源的接入，净负荷的不确定性进一步增强，所以电力系统净负荷是一组典型的非线性时间序列。本文针对净负荷的这一特性，基于并入分布式光伏的电力系统，对其线性成分和非线性成分分别进行预测。首先利用ARIMA模型对线性成分较强的跟踪能力，利用净负荷历史数据建立线性成分分析模型，形成包含净负荷序列非线性成分的残差序列；其次，使用CC法对历史数据拟合残差进行相空间重构，并将重构后的残差使用SVR模型进行训练，建立非线性成分预测模型。最后将线性成分预测结果与非线性成分预测结果合并得到净负荷的最终预测数据。

从分析结果来看，提出的预测方案将2种模型进行组合，充分利用各自优点来克服彼此的不足，可以较好适应电力系统净负荷强烈的非线性特性，且对净负荷预测精度较高。

1 基本原理

1.1 自回归滑动平均模型

自回归滑动平均模型的基本原理是把时间序列视为一个随机过程，建立数学模型来描述或模拟，可以良好的反应时间序列线性成分的动态特征和持续特性，揭示出时间序列过去于现在及将来与现在的相互关系。一般表示为ARIMA（p,q,d），其中p为自回归模型（AR模型）阶数，q为滑动平均模型（MA模型）阶数，d为差分处理阶数。ARIMA（p,q,d）的一般表达式如式（1）

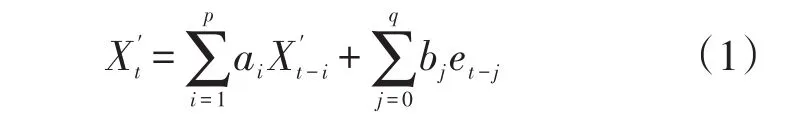
式中:ai为自回归系数；bj为滑动平均系数；et-j是白噪声序列，为独立误差。

ARIMA（p,q,d）的建模步骤:

（1）差分处理:对原始序列［Xt］进行d阶差分处理得到平稳时间序列［］；

（3）参数估计:利用相关矩进行ai和bj的参数估计，确定最终ARIMA（p,q,d）模型；

（4）数据预测:通过建立的ARIMA模型实现单步或多步预测。

1.2 CC法相空间重构

相空间重构也叫动力系统重建，即通过一维的时间序列反向构造出原系统的相空间结构，找到原动力系统隐藏的演化规律［1］，更好地反应实际系统的高维特性。假设原始时间序列为{x (k),k=1,2,…,N} ，那么在相空间中重构的一点的状态量可表示为

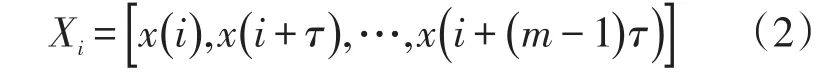
式中:m为嵌入空间维数；τ为时间延迟。

重构相空间技术的关键在于正确的选取嵌入空间维数m和时间延迟τ。CC法相空间重构以m和τ的选取是相互依赖的为理论基础，同时计算出二者的值。该方法具有容易操作，计算量小且具有较强的抗噪声能力。本文采取该方法对相关样本进行相空间重构。

该方法的具体执行步骤如下:

（1）将原始时间时间序列{x (k),k=1,2,…,N}分解成t个互补重叠的子序列，t为重构时延，即

式中:N为t的整数倍。

（2）对每个子序列计算关联积分

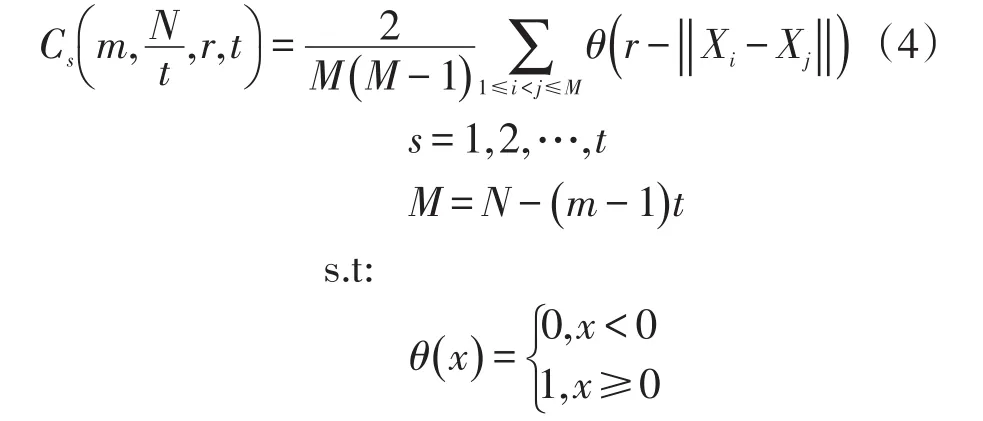
式中:M为重构相空间状态量个数；θ()·为Heavisde单位函数，根据BDS统计结论，取m=2,3,4,5，对应r=0.5σ,σ,1.5σ,2σ，σ为时间序列标准差。

（3）采用分块平均策略计算检验统计量

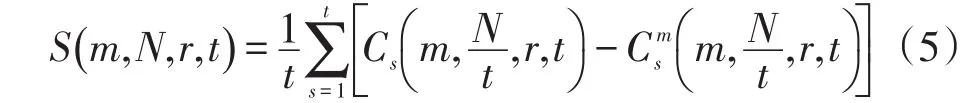
（4）计算差量

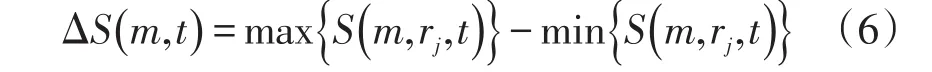
ΔS(m ,t)度量了S(m ,N,r,t)对半径r的最大偏差。当ΔS(m ,t)为最小值时，此时重构相空间中的点接近均匀分布，重构系统的轨道在相空间完全展开，时间序列的相关性最接近于零。因此ΔS(m ,t)～t曲线反映了原始序列的自相关特性。

（5）计算

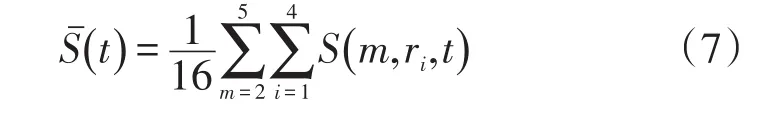
1.3 支持向量回归

SVR是SVM用于回归建模的方式，作为一种机器学习算法，目前广泛应用于预测和拟合等方面，其核心思想在于构建分类超平面，并且保证离超平面距离最近的样本与超平面之间的距离最大。对于两分类问题:被最优分类超平面w·x+b=0完全无误地分为2个类别。因此，构造最优超平面问题转化为优化问题

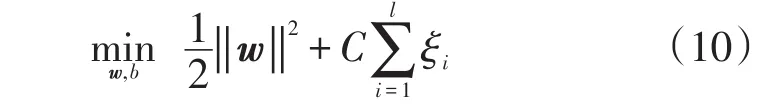
约束条件为

式中:w为最优超平面法向量；b为阈值；C为惩罚参数；ξi为松弛变量。可以利用拉格朗日乘子法对上述问题求解。若扩展到非线性问题，可以利用映射φ(x)将低维空间中的样本映射为高维空间中，此时目标函数为

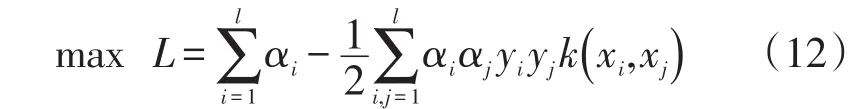
式中:αi为拉格朗日乘子。

SVR将线性不可分的输入样本空间映射到高维空间实现线性回归，得非线性回归函数 f(x)=wTφ(x)+b。利用拉格朗日乘子法进行求解。一般情况下，核函数的选择中高斯核函数较多，其中σ为高斯核参数。

2ARIMA⁃CC_SVR模型

2.1 母线净负荷计算

从系统侧看，母线净负荷即某时刻母线负荷与相应时刻分布式电源出力之差［15］，即

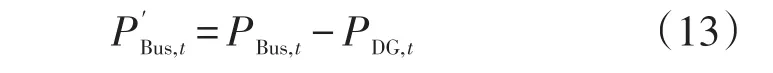
2.2 ARIMA⁃CC_SVR建模步骤

电力系统净负荷受自然、社会以及各种突发情况的影响，是一种复杂的非线性时间序列，具有周期性、非线性以及突变性，不能具体的描述为单纯的线性非线性系统。考虑到ARIMA对线性系统以及SVR对非线性较强的预测处理能力，再因为单一的净负荷时间序列不能充分反映电力系统负荷情况的动态特性，且不满足SVR对数据的要求，本文提出了ARIMA模型和基于相空间重构的SVR相结合的净负荷预测模型，其工作原理如图1所示。

电力系统净负荷数据 {pt,t=1,2,…,M }包含着线性成分和非线性成分，则可以将其视为由线性部分{lt,t=1,2,…,M} 和 非 线 性 部 分{nt,t=1,2,…,M}组成，则净负荷可以描述为

基于ARIMA⁃CC_SVR模型的净负荷预测具体建模及预测步骤如下:

（1）确定ARIMA（p,q,d）参数，基于ARIMA对净负荷线性部分lt进行预测，预测结果为，残差为 nt，即

式中:残差序列{nt,t=1,2,…,M} 包含净负荷序列{pt,t=1,2,…,M }的非线性关系。

（2）基于CC法对ARIMA（p,q,d）模型残差序列{nt,t=1,2,…,M} 以嵌入空间维数m和时间延迟τ进行相空间重构，得到重构之后的相空间矩阵为

（3）基于重构后的残差矩阵利用SVR建立净负荷非线性部分预测模型。假设训练样本有k+1个，则训练的输入矩阵X和输出矩阵Y分别为式（17）和（18）所示。预测阶段则将作为SVR模型的输入，则此时SVR模型的输出Y′=nk+2即为净负荷非线性成分的预测结果，记序列{n^t}为净负荷非线性成分的预测结果。

图1 ARIMA⁃CC_SVR工作原理图

（4）净负荷预测结果

3 预测结果与分析

为验证ARIMA⁃CC_SVR净功率预测模型的有效性，本文选取某市220 kV变电站采集的2017年5月份10天的母线总功率和接入该母线的分布式光伏出力数据，分布式光伏安装容量约为50 MW，基于Eviews8.0和MATLAB8.2对提出模型进行验证，数据的实时监测采样周期为5 min。选取样本中前7天数据进行预测模型建模，后3天数据作为预测数据，下面给出数据样本后3天的预测结果并对结果进行分析。

3.1 ARIMA（1，1，1）模型预测结果

用样本前7天的净负荷数据进行建模，图2为预测模型对样本中后3天净负荷的预测结果。

从图2中可以看出ARIMA模型可以较好的预测出净负荷变化的整体趋势，也就是对净负荷时间序列的线性部分可以达到较好的预测精度。可以明显发现，当净负荷波动比较剧烈时，ARIMA预测结果并不能真实反映净负荷的真实情况。

图2 ARIMA模型预测结果

3.2 CC相空间重构，嵌入空间维数m和时间延迟τ的确定

对于确定的样本空间，CC法的嵌入空间维数m和时间延迟τ是确定的。、Scor(t)和t的关系曲线如图 3，可以确定 τ=7 ，tω=22 ，根据tω=(m -1) τ可以确定嵌入空间维数

图3和t的关系曲线

3.3 ARIMA⁃CC_SVR模型预测结果

对ARIMA（1，1，1）模型预测残差以m=5，τ=7进行相空间重构，使用SVR模型对重构残差进行建模以预测，使用交叉验证法对SVR参数进行优化，最终选不敏感系数ε=0.001，惩罚系数C=100，ARIMA⁃CC_SVR模型预测结果如图4所示，经过相空间重构的SVR预测之后，预测结果对波动性较强的净负荷情况得以改善，说明本文提出的预测方案可行。

图4 ARIMA⁃CC_SVR模型预测结果

为评价含分布式光伏系统净负荷的预测效果，本文采用平均绝对百分误差εMAPE和均方根误差εRMSE来衡量整体误差程度以及预测值与真实值之间的偏离程度

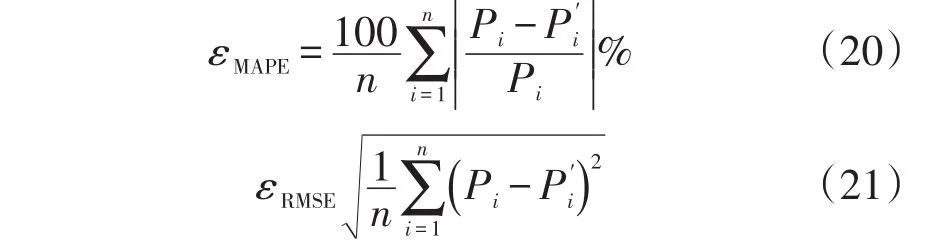
预测精度如表1所示。从表1中可以看出本文提出的ARIMA⁃CC_SVR预测模型比单纯的使用ARIMA模型的整体预测精度明显提高。进一步分析净负荷波动强度不同的情况，不同波动情况下的预测精度如表2所示，从表2可以看出，本文提出的预测方案对于不同程度的波动的净负荷情况，预测精度均有明显改善。

表1 预测精度

表2 不同波动情况下的预测精度

综合预测结果及模型本身的特点，对本文提出的净负荷预测模型进一步阐述:

（1）ARIMA模型对波动性不强即非线性成分不明显的时间序列预测精度较高；

（2）相空间重构可以构造出原动力系统的相空间结构，更好的反应原动力系统的内部联系。CC法相空间重构以嵌入空间维数和时间延迟的选取是相互依赖的为理论基础，计算量小、可靠性高且抗噪能力较强；

（3）SVR模型对非线性变化有较强的跟踪与捕捉能力，可以有效分析净负荷的非线性成分；

（4）ARIMA⁃CC_SVR预测模型考虑到净负荷线性与非线性对预测模型的要求，采用分别建模再合并的综合分析方法，保证了预测模型的完备性，并提高了净负荷预测预测精度。

4 结论

（1）相对于传统的净负荷预测技术，本文采取了对净负荷非线性及线性成分分别提取的预测方案，不管是针对平稳还是波动性较强的净负荷情况，均可取得较好的预测效果。

（2）本文提出的ARIMA⁃CC_SVR预测模型充分利用ARIMA模型对线性变化的较强追踪能力以及SVR对非线性变化较强的捕捉能力，针对单一数据情况，运用CC法进行原动力系统重建，实现了混合建模。

（3）本文通过对含分布式光伏电站净负荷的预测分析，验证了模型的有效性。对于不同的含有分布式光伏的配电网，其分布式光伏的渗透率可能不同，但本文所提的净负荷预测方法从净负荷本身出发建模，对于不同渗透率情况仍然适用。

［1］ 郑永康.相空间重构与支持向量机结合的短期负荷预测研究［D］.成都:西南交通大学，2008.

［2］ 肖白，聂鹏，穆钢，等.基于多级聚类分析和支持向量机的空间负荷预测方法［J］.电力系统自动化，2015，39（12）:56-61.

［3］ 刘文颖，门德月，梁纪峰，等.基于灰色关联度与LSSVM组合的月度负荷预测［J］.电网技术，2012，36（8）:228-232.

［4］ 孙谦，姚建刚，赵俊，等.基于最优交集相似日选取的短期母线负荷综合预测［J］.中国电机工程学报，2013，33（4）:126-134+17.

［5］ Yaclan Y,Bican B.Empirical mode decomposition based denoising method with support vector regression for time series prediction A case study for electricity load forecasting［J］.Measurement,2017，103:52-61.

［6］ 马静波，杨洪耕.自适应卡尔曼滤波在电力系统短期负荷预测中的应用［J］.电网技术，2005，29（1）:75-79.

［7］ 王德文，孙志伟.电力用户侧大数据分析与并行负荷预测［J］.中国电机工程学报，2015，35（3）:527-537.

［8］ 王保义，赵硕，张少敏.基于云计算和极限学习机的分布式电力负荷预测算法［J］.电网技术，2014，38（2）:526-531.

［9］ 汤庆峰，刘念，张建华，等.基于EMD⁃KELM⁃EKF与参数优选的用户侧微电网短期负荷预测方法［J］.电网技术，2014，38（10）:2691-2699.

［10］ Sepasi S,Reihani E,Howlader AM,et al.Very short term load forecasting of a distribution system with high PV penetration［J］.Renewable Energy,2017，106:142-148.

［11］ 钟清，孙闻，余南华，等.主动配电网规划中的负荷预测与发电预测［J］.中国电机工程学报，2014，34（19）:3 050-3 056.

［12］ Kaur A,Nonnenmacher L,Coimbra C F M.Net load forecasting for high renewable energy penetration grids［J］.Energy,2016，114:1 073-1 084.

［13］ 沈沉，秦建，盛万兴，等.基于小波聚类的配变短期负荷预测方法研究［J］.电网技术，2016，40（2）:521-526.

［14］ 曾鸣，李娜，王涛，等.兼容需求侧资源的负荷预测新方法［J］.电力自动化设备，2013，33（10）:59-62+73.

［15］ 颜宏文，李欣然.基于差分进化的含分布式电源母线净负荷预测［J］.电网技术，2013，37（6）:1 602-1 606.