省级用电市场发展态势综合量化评估分析方法研究

杨晓梅，李艺丰，王蓓蓓，胡晓青，孔 林，潘 璐

（1.国网江苏省电力公司，南京 210024；2.东南大学电气工程学院，南京 210096；3.国网无锡供电公司，江苏 无锡 214000；4.国网秦皇岛供电公司，河北 秦皇岛 066000；5.悉尼大学工程和信息技术学院，悉尼 2008）

2015年，中共中央、国务院发布《关于进一步深化电力体制改革的若干意见》（中发〔2015〕9号）［1］（以下简称“9号文”），对我国新一轮电力体制改革作出了总体部署。国家发改委、能源局又发布了电力体制改革的6个配套文件，涉及输配电价改革、电力市场建设、电力交易机构组件、放开发用电计划、售电侧改革、燃煤自备电厂监管等内容［2］，重点解决了9号文提出的“三个放开，一个独立”（即有序放开即有序放开输配以外的竞争性环节电价，有序向社会资本开放配售电业务，有序放开公益性和调节性以外的发用电计划，推进交易机构相对独立、规范运行）的具体实施问题，利于有序开展各项试点工作。

其中在售电侧的改革，将强化竞争机制成立售电公司，允许民间资本进入，形成市场化的售电新机制。由于电力公司有向全体用户供电的义务，在改革的过程中，需要有售电商为没有选择售电商的用户提供售电服务，即保底服务。因此，对于评估电力行业的电量消费现状时也需要考虑更多的影响因素。同时，在电力消费的运行过程中，又不能简单的只从用电量增速这一指标来看到行业用电的发展好坏，要正确地把握用电市场的发展趋势及规律，还需要进一步考虑到多方面电力需求影响因素，挖掘出电力需求与经济发展的内在联系及本身的波动趋势，将有助于指导电力系统运行规划，为相关部门选择相应的策略提供了切实可靠的依据。

目前，国内外学者对能源消费与经济之间的相关研究已经取得了丰富的理论和应用成果。文献［3］利用中国1954—2003年的年度数据，对能源总消费、煤炭消费、石油消费、天然气消费以及水电力消费等进行了协整性分析；文献［4］对我国电力消费与经济增长之间的关系进行了协整分析和格兰杰因果关系检验，并建立误差修正模型，研究结果表明，两者之间在长期和短期都存在着双向格兰杰因果；文献［5］利用中国1953—2003年的年度数据，对与能源总消费、煤炭消费、石油消费、天然气消费以及水电力消费等进行了实证分析，结果表明，存在GDP与能源消费总量之间的协整关系；文献［6］利用Granger因果关系和误差修正模型对10个主要工业部门的用电量与GDP之间的双向因果关系进行了分析。但国内大多数［7—10］研究所涉及的经济因素比较片面单一，在国内目前复杂多变的态势下，应引入更多的经济指标来分析其和能源消费之间的关系。

基于此背景，本文将针对省级用电市场，将季节调整、多元统计分析方法中的主成分分析方法以及生产函数引入评价分析中，重点筛选出和电力消费所相关的指标数据，并用季节调整的方法剔除季节性波动和其他随机因子，筛选出反映其真实规律的数据；其次使用主成分分析方法实现聚类分析，建立因子得分模型；最后基于改进的柯布-道格拉斯生产函数，来量化各类经济指标对用电量的影响程度，以此反映经济社会与用电市场的内在联系。

1 研究思路

本文研究的出发点将针对省级用电市场，在其电网公司处在动态的、不确定的、复杂的外部环境的背景下，收集整理各类经济、电量等外部环境指标，帮助公司分析量化各类指标对其核心指标——全社会用电量的影响程度，并从时间维度来分析各类指标的影响程度变化趋势规律。

图1给出了本文设计的外部环境指标影响量化分析流程图。

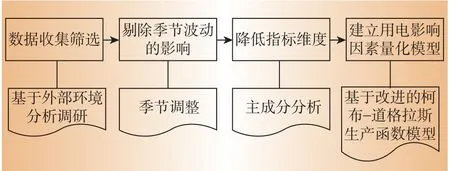
图1 分析预测方法流程图

2 理论模型建立

2.1 季节调整

季节调整是一个数学过程，通过这个过程，将循环的季节因素的影响从一个经济的时间序列中剔除出去。季节因素是经济时间序列中每年重复出现的循环变动，天气、风俗、政策等因素的影响都会引起季节性波动。季节性波动的复杂性会掩盖经济发展过程中的客观规律，使序列的预测变得复杂、困难，因此要将季节因素和其他随机因子从原序列中剔除，这就是季节调整。目前季节调整最常用的方法是X11方法［11］，而本文选用的X12方法是在X11方法基础上发展而来，可将电量分解为趋势循环项、季节项和随机因子3个部分。并逐步剔除季节项以及随机因子，确定最终趋势循环项，将其作为经过季节调整后的数据。

2.2 主成分分析

在实际研究中，多指标问题是经常遇到的，而且在多数情况下，不同指标之间具有一定的相关性，这势必增加问题分析的复杂性。主成分分析就是设法将原来的指标重新组合成一组新的互相无关的几个综合指标来代替原来的指标，同时，根据实际需要从中取几个较少的综合指标，尽可能多地反映原来指标的信息。由于主成分分析法能浓缩信息，简化指标的结构，使分析问题的过程简单、直观、有效，所以被广泛应用于各个领域［7］。

因子得分是主成分分析的最终体现。当因子成分确定以后，便可以根据主成分得分模型计算各主成分在每个指标上的具体权重，从而得到各个主成分得分。这里假设用F1、F2、…、Fm表示，其中X1、X2、…、Xn为分析指标

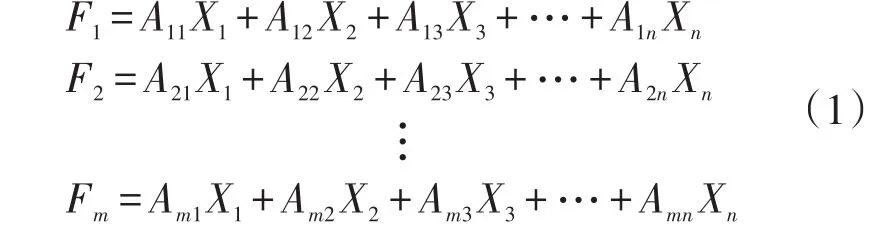
设公因子F1、F2、…、Fm的估计值即因子得分，各公因子的特征值为 λ1,λ2,…,λm，表明每个公共因子对原始数据的解释能力，所以通过贡献率构造评价分析模型

这里可以根据因子得分来代替原始变量，达到数据降维的效果，y则可以当作该类指标组的代表变量。

由于主成分分析完全没有参数限制，其结果仅与原数据有关，不存在主观因素，因此已经在输电网规划决策［12］、负荷预测［13］、暂态稳定评估等方面成功运用。

2.3 改进的生产函数模型

在西方经济学中，生产理论是最重要内容之一；同样，在西方的计量经济学中，生产函数模型的研究与发展始终是一个重要的、最活跃的领域，其在数理经济学与经济计量学的研究与应用中都具有重要的地位。生产函数模型是指在一定时期内，在技术水平不变的情况下，生产中所使用的各种投入的生产要素的数量与所能生产的最大产量之间的相互关系。

柯布-道格拉斯生产函数最初是美国数学家柯布（C.W.Cobb）和经济学家道格拉斯（P.H.Douglas）共同探讨投入和产出的关系时创造的生产函数，是在生产函数的一般形式上作了改进，引入了技术资源这一因素。他们认为在技术经济条件不变的情况下，产出与投入的劳动力及资本的关系可以表示为

式中:Y为产出总量；A为常数，也称效率系数；K和L分别为投入的劳动量和资本量；α和β分别为劳动力和资本的产出弹性系数，说明当投入的劳动力增加1%时，产出平均增长β%；当资本投入增加1%时，产出平均增长α%。

同样，原有的柯布-道格拉斯生产函数已经不能再适应新的经济发展形态，在工业时代用以衡量生产力水平的产量，资本投入量和劳动力投入量已经不能完全适应信息时代的生产力发展水平了。综合上述原因，需要对柯布-道格拉斯生产函数做出一定的改进修正，使之适用于量化评估电力市场影响因素，因此改进后的柯布-道格拉斯生产函数为

选取2017年7—10月在我院治疗的肺心病患者72例作为研究对象。1）纳入标准：由医师筛选符合肺心病诊断标准，不限年龄、种族、地区，并取得知情同意，并经治疗后，病情好转，成功出院的患者；2）排除标准：心、脑、肾等重要脏器有明显功能障碍，及精神障碍、妊娠以及合并其他肺部疾病患者，以及拒绝参加此研究者。将72例患者采用随机数表法分为实验组及对照组。实验组中，男30例，女6例；年龄46～81岁，平均年龄为（59.280±5.612）岁，对照组中，男27例，女9例；年龄42～79岁，平均年龄为（60.650±5.932）岁。两组患者的一般资料对比，差异无统计学意义（P＞0.05），具有可比性。

为了便于分析，对式（2）两边取对数，使等式线性化，从而得到如下方程

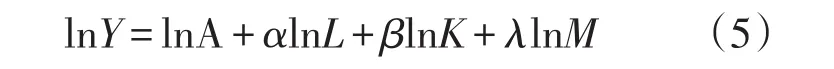
式中:Y为用电量；L为生产资料投入；K为资本投入；M为工业产销投入；即通过生产函数测算，可以获取工业产销、资本投入、生产资料要素产出弹性等量化用电市场影响因素的数值，最终结合时间跨度完成对用电市场发展水平的综合评定。

2.4 评价指标体系

根据上述理论模型的需求，针对省级用电市场，为实现量化外部环境因素对其影响程度的目的，需要建立一套较为全面完善的影响因素指标体系。根据从统计局、电力公司收集到的各类指标数据，建立了表1中的省级用电市场影响因素评价指标体系。

3 用电影响因素量化分析计算流程

用电影响因素量化计算流程如图2所示。

首先，收集外部环境下各类经济指标、电量指标数据，并按照不同投入类型对其进行归类；利用2.1节季节调整方法将天气、节假日等季节因素和其他随机因子从原序列中剔除；采用min⁃max标准化方法对调整后的数据进行处理，将其转化为无量纲的数值；然后利用2.2节主成分分析法分别对3类投入指标组进行聚类，并利用因子得分模型，构造出代表各类指标组的3类投入因子；最后基于2.3节改进后的柯布-道格拉斯生产函数模型对其进行分析，得到各类投入对其产出的影响量化程度，并可从不同的时间跨度中分析影响程度的变化趋势规律，深入挖掘出3类投入指标组下面每个细分指标对产出的影响程度，实现精细化分析。

表1 省级用电市场影响因素指标体系

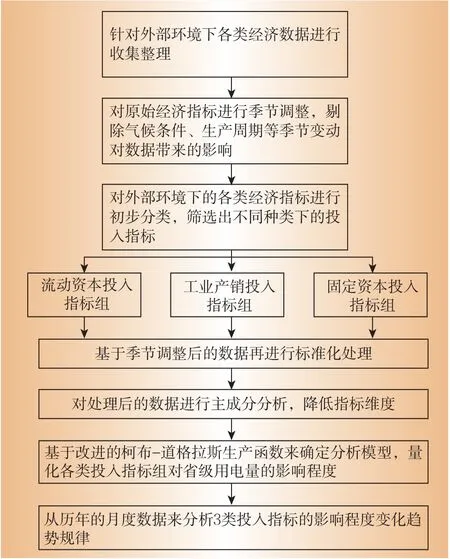
图2 分析计算流程图

4 算例分析

4.1 阶段量化程度分析

选取我国东部沿海某省作为典型实例，收集各类经济、电量数据进行分析，时间跨度选为2011年1月—2015年9月，目标变量将选取全社会用电量，影响变量均选取生产资料投入指标、工业产销投入指标、资本投入指标，从整体上量化一定时间阶段内各类投入对目标的影响程度。

依据设计的计算方法步骤，首先对3个投入指标组中每个细分指标的原始数据进行季节调整，其次，通过SPSS软件对每个指标组进行主成分分析。因篇幅所限，这里仅选取工业产销投入指标组作为主成分分析的典型实例，根据主成分分析方法，得到特征值以及公因子的方差贡献率和累计方差贡献率如表2所示。从表2中可知该指标组下可提取2个公因子，累计反映各变量综合信息为98.8%，这样就在损失很少信息的前提下把多个指标转化为几个不相关的综合指标。

表2 公因子的特征值、方差贡献率和累计方差贡献率

借助因子得分模型来代替原始变量，建立工业产销投入指标组的代表变量M。同理可以得到资本投入指标组的代表变量K以及生产资料投入指标组的代表变量L，其次就可以把M、L、K3个代表变量代入到改进后的柯布-道格拉斯生产函数中，可得式（6）

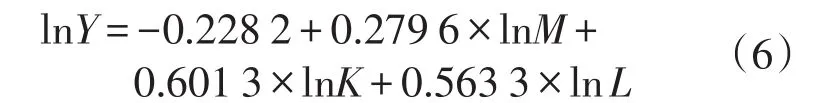
改进后的柯布-道格拉斯生产函数通过了显著水平为0.05的t检验和F检验，说明可信度较强。修正的样本可决系数为0.952，表明工业产销投入、固定资本投入和流动资本投入对全社会用电量增长的解释能力为95.2%，很高的解释能力表明模型很好地拟合了样本数据。

此外，从式（6）可知偏斜率系数0.601 3表示全社会用电量对资本投入的弹性，即在工业产销投入和流动资本投入保持不变的条件下，固定资本投入每增加一个百分点，全社会用电量将增加0.601 3个百分点，其影响程度要明显大于工业产销投入和生产资料投入对全社会用电量增长的影响程度，可见资本投入对全社会用电量增长的影响最为显著。

4.2 细分指标影响程度分析

基于4.1节阶段量化程度分析所得到的结论，深入探究各类投入指标组内细分指标对目标变量的影响程度，这里将根据因子得分模型即式（1），并结合生产函数方程式（6）来实现精细化分析。整理得每个细分指标对全社会用电量的影响程度见表3，即每个指标增加1%时，对应用电量将会增加x%，其中x为表中指标对应数值。

从表3可以看出，在2011年1月—2015年9月期间，对该省下全社会用电量影响程度最大的是化肥产量，其每增加1%，用电量将增加0.235 6%，其次为水泥产量，对应全社会用电量增加0.1531%，生产资料投入组中指标均为高耗能产品，在其生产过程中需要消耗大量的电能，且其电能消耗则直接反应于产品产量，故生产资料投入对用电量的影响程度较为明显。而在资本投入指标中，制造业投资对用电量影响程度最大，这也与该省是闻名全国的制造业大省的现状相符，其制造业产业总体规模大，有活力，基础好，因此该省若想提高用电发展水平，必须重视该地区设备制造业等相关行业的发展。

4.3 影响程度趋势分析

为了反映工业产销投入、固定资本投入和流动资本投入在不同阶段下对全社会工业用电及工业用电的影响程度，特选取东部沿海该省在2011年—2015年间的月度数据，将按照每半年的阶段周期对其进行分析，结果如图3所示。

从图3可以看出，从2011年到2015年间，3类投入指标组对全社会用电量增长的影响程度均呈下降趋势，这就与在这5年间国家产业发展环境和策略息息相关，2011年作为“十二五”的开局之年，又是中国经济战略性调整的转型“元年”，并且5年间国际环境错综复杂，世界经济贸易增速不断滑落，金融市场不断震荡。因此，在逐渐低迷的外部环境影响下，3类投入对用电量的影响程度也会随之下降。

表3 细分指标影响程度汇总

图3 3类投入指标组影响程度走势图

其中，生产资料投入对用电量的影响程度下滑最为明显，其指标均为耗能较大的行业产量，图3中趋势也反映出5年中此类高耗能产品的日渐低迷发展态势。伴随着国家大力推进产业结构调整转型，以及9号文的出台，逐渐遏制高耗能行业的发展势头，单位产品能耗不断下降，节能降耗成效明显。

而工业产销投入代表该省工业经济的生产规模，工业经济在“十二五”之间处在一个下行的区间，并且伴随经济结构调整，其对全社会用电量的影响程度将不可避免的呈现出下降的趋势，维持在较低的水平上。在资本投入上，投资结构不断优化，其中，高耗能投资占比继续下降，而高技术产业投资和服务业投资增长速度领先，且占比也在不断提高。

5 结论

随着新电改政策的不断推进，在此背景下，本文将季节调整、多元统计分析方法中的主成分分析方法以及生产函数引入评价分析中，并选取我国东部沿海某省作为实例分析。算例结果证明:①通过对季节调整后的指标数据进行主成分分析，再基于改进的柯布-道格拉斯生产函数可以确定每个投入指标组对用电量的影响程度；②根据因子得分模型可以深入分析量化各个细分指标对用电的影响程度，有助于电网企业对用电形势的变化进行更精细化的分析；③可反映在不同阶段下各个指标的影响程度的变化趋势，可为未来的保底服务政策、节能减排、地市发展规划等相关决策提供依据。

［1］ 中华人民共和国国务院.关于进一步深化电力体制改革的若干意见（中发〔2015〕）［Z］.2015-03-15.

［2］ 国家发展改革委，国家能源局.关于印发电力体制改革配套文件的通知（发改经体〔2015）〕）［Z］.2015-11-26.

［3］ 马超群，储慧斌，李科，等.中国能源消费与经济增长的协整与误差校正模型研究［J］.系统工程，2004，22（10）:47-50.

［4］ 王海鹏，田澎，靳萍.中国电力消费与经济增长的变参数协整关系［J］.华北电力大学学报，2005（4）:48-51.

［5］ 贲兴振，杨宝臣.中国能源消费与经济增长的协整关系分析［J］.哈尔滨理工大学学报，2005，10（4）:117-120.

［6］ 何永秀，赵四化，李莹，等.中国工业用电量与经济增长的关系研究［J］.工业技术经济，2006，25（1）:78-82.

［7］ 张兴平，牛玉琴，赵旭.中国电力消费协整关系模型［J］.中国电机工程学报，2008，28（13）:114-119.

［8］ 谢品杰，谭忠富，侯建朝，等.我国城市化与电力消费水平的动态关系分析［J］.电网技术，2009，33（14）:72-77.

［9］ 李强，王洪川，胡鞍钢.中国电力消费与经济增长——基于省际面板数据的因果分析［J］.中国工业经济，2013（9）:19-30.

［10］ 张龙.宏观经济与用电量关系辨析［J］.中国电力企业管理，2012（8）:40-43.

［11］ 郭琦，项静恬.经济时间序列的X-11季节调整方法［J］.数理统计与管理，1993（3）:52-63.

［12］ 聂宏展，聂耸，乔怡，等.基于主成分分析法的输电网规划方案综合决策［J］.电网技术，2010，34（6）:134-138.

［13］ 程其云，王有元，陈伟根.基于改进主成分分析的短期负荷预测方法［J］.电网技术，2005，29（3）:64-67.