计及电动公交车-电池联合调度的公交换电站有序充电策略

李笑蓉，陶 冀，丁健民，程 瑜

（1.国网冀北电力有限公司 经济技术研究院，北京 100038；2.华北电力大学 电气与电子工程学院，北京 102206）

随着经济发展和城市化进程的推进，汽车数量不断增长所导致的气候变化和环境污染问题，在日益挑战着传统的交通出行方案。近年来，电动汽车代替传统燃油汽车已成为汽车工业的重要发展方向，并在公共交通得到了有力地推广。发展电气化公共交通已成为我国交通能源转型和升级的重要举措［1］。

电动公交的电能补给方式包括充电和换电2种模式。电动公交车通常使用统一规格电池，并且统一管理，具备较好的条件以采用换电模式。换电模式下，公交车在换电站内通过电池更换设备将满电的电池装入车中，完成换电过程后，即可驶离换电站，继续运营，换电时间一般在10 min左右，对公交车正常运营的影响较小。电动公交的电能可靠补给直接影响到人们乘坐公交车出行的安全和舒适度。同时，换电模式下公交车更换下的电池充电计划有一定的灵活安排区间，可以作为用户侧的需求响应资源，减少电动公交大规模普及引起的新增充电负荷对电网负荷峰谷特性的负面影响。故本文以电动公交采用换电模式为背景，考虑电动公交车和电池的联合调度需求，研究电动公交换电站的有序充电策略。

目前，国内外对于电动汽车充换电设施的研究主要包括选址规划［2—5］和优化运行［6—9］。专门针对电动公交充换电设施的规划和运行的优化策略研究相对较少。基于电动公交整车充电模式，文献［10］研究了充电需求，分析了车速、载客量对电动公交充电站充电需求的影响。文献［11］研究了快充式公交充电站的优化运行，基于对进站电动公交车的进出站时间和荷电状态的实时采集，优化安排充电计划。基于电动公交换电模式，文献［12］分析了电动公交的日换电电量需求，建立了减小充电成本和负荷波动的换电站优化运行模型。文献［13］基于给定的换电需求，计及分时电价影响，以全天充电电费最低为目标，研究换电站的优化运行。文献［14］针对电池集中配送模式下的电动公交的换电站和电池充电站的优化规划问题进行了研究，文中根据日油耗量测算换电电量需求和次数。电动公交充电负荷在城市10 kV配电网络中负荷水平相对较大，电动公交充换电站的配电容量通常达到6 000 kVA左右，大规模电动公交充电负荷接入必然对配网运行产生影响。文献［15］提出太阳能与电动公交车换电站联合建设运营模式，以发挥电动汽车对电网的填谷作用。文献［16］强调了馈电线路容量对电动公交充电计划安排的影响，研究了馈线上的电动公交车运营总数量的最大值。

为更精准预测和调控电动公交的充电负荷，有必要充分计及公交车调度计划和电池换充计划的时序特征，对车和电池的运行状态进行更细化地模拟。故本文基于换电模式，计及电动公交换电站的充、换电设施和电池备用数量的影响，联合模拟电动公交车调度计划与电池换充计划，以降低峰谷差为优化目标，建立电动公交换电站有序充电决策模型，以分析优化调控下的电动公交充电负荷水平。

1 公交车状态转换时序分析模型

式中:符号ceil为向上取整操作。

在线路上运营的公交车可分为3种状态:“等待发车状态”、“行驶中状态”以及“换电状态”。这3种状态的转换过程为下面4种场景:①公交车发车，从“等待发车状态”转换为“行驶中状态”；②公交车到站，且剩余电量能够支撑其下一次发车运行一圈后回到起点，则公交车进入“等待发车状态”；③公交车到站，剩余电量不满足下次发车电量需求，则公交车从“行驶中状态”转换为“换电状态”；④公交车更换电池完成，“换电状态”结束，进入“发车等待状态”。其状态转换过程如图1。

某线路公交车从公交场站出发，运行一圈后回到场站。换电站位于线路所在的公交场站，对公交车进行电能补给。考虑电动公交运营首末车时间、单程行使里程、发车间隔、换电时长等因素，建立公交车状态转换时序模型，全过程模拟每辆车的进、出站时间和SOC值，从而可仿真一天内电动公交车换电需求产生的时间分布。

1.1 公交车数目计算及其状态转换

公交车运行一圈的时间为Trun，换电站更换电池的时间为Tswap，发车间隔为Tgap，为保证公交车正常运行，则本条线路所需的最小公交车数目N1为［17］

图1 公交车状态转换过程图

1.2 公交车状态转换时序分析流程

电动公交车换电需求产生时刻的分析流程图如图2所示，仿真流程以分钟为单位时间间隔，仿真周期为一天，仿真车辆i从1到N1，具体步骤如下:

（1）判断时刻t是否为发车时刻。根据公交车调度计划，初始化公交车首班车和末班车的发车时间，仿真流程中，从运营开始时间Tst开始，到运营结束时间结束，逐时采用式（2）判断是否为发车时刻，若满足式（2），则t为发车时刻

式中:符号mod为求余操作。

（2）选择发车车辆，实现场景1。采用顺序发车，选取等待发车队列中等待时间最长的车辆 j发车，车辆 j满足式（3）

式中:j=1,2,…,N1；Fj表示车辆 j是否处于等待发车状态，Fj为1，表示处于等待发车状态；Fj为0，代表车 j不处于等待发车状态。运营起始时刻每辆车Fj均为1。为第 j辆车在发车队列里的等待发车时间，根据各时刻点减去此车进入等待队列时间得，初始值为0。

选择车辆 j发出后，将车辆 j从等待发车队列中剔除，并生成车辆 j的预计到站时间和预计到站SOC值，如式（4）所示

式中:c为电动公交车单位里程耗电量；L为运营一圈的里程；C为满电状态下的电池容量。

（4）判断时刻t到站车辆是进入等待发车状态或是换电状态，即是进入场景2或场景3。判断到站车辆i的SOCi是否足以支持下一趟运行，当满足式（5）时，表明剩余电量不能支撑下一圈公交运营，公交车需要换电，实现场景3。

式中:SOCwarn为电池SOC警戒值。

如判断时刻t到站车辆需进入换电状态，则生成换电需求产生序数k，k初始值为0，每次有车辆进入换电状态时更新k=k+1，生成第k次换电需求产生的时刻Tk，如式（6）；并生成第i辆车预计换电结束时刻，如式（7）

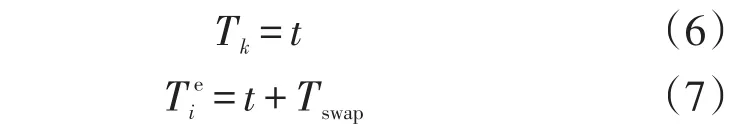
当时刻t到站车辆i的SOCi足以支持下一趟运行时，即不满足式（5），将此车加入等待发车队列，Fi设为1，并记录此车进入等待队列时间，实现场景2。

（6）t=t+1，循环上述步骤，至t到结束时刻。

（7）统计输出换电需求产生总次数M和每次换电需求产生时刻=1,…,M )。

2 换电站有序充电模型

图2 公交车状态转换时序分析图

电动公交配置的电池数量是影响其充电负荷有序充电调控潜力的关键因素。换电模式下某条线路电动公交配置的电池数量至少要满足保障公交车调度计划的最小规模。在大于最小规模的电池配置方案下，电动公交换电站的充电计划安排具有一定的有序充电的调控裕度。

2.1 电池配置数目最小需求

换电站需要配置的最少电池数目取决于换电站保证电动公交正常运行的需要，即每次换电需求产生时，换电站必须至少能够提供一组满电电池以供更换。电动公交车数目为N1，每辆公交车上配备一组电池，此外，换电站配置备用电池组数目为N2，电动公交运营配置的电池组总数为N1+N2。换电站遵循先到站的空电池充满电后优先服务的原则，则第k次换电更换下来的空电池最早可以开始充电的时间t1(k) 如式（8）

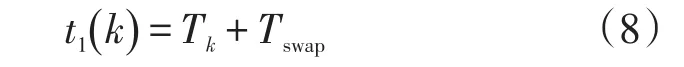
式中:Tk为第k次换电需求产生时刻，根据第1节电动公交车状态转移时序分析模型获得。

第k次换电更换下来的空电池最晚可以开始充电的时间t2(k) 如式（9）

式中:Tcharge为一组电池从警戒SOC充至满电所需的时间。

为了保障在第一次换下的电池充电期间产生的换电需求，换电站需要额外配置备用电池组。换电站需要配置的最小备用电池组数根据第一次换下的电池组充满电之前的有待满足的换电次数决定，即在时刻T1+Tswap+Tcharge到来之前所发生的换电需求次数为换电站需配置的备用电池组N2的最小数目需求N2,min，表示如式（10）

式中:符号index为提取数组中某元素的项数操作。

当换电站配置的备用电池组数目为最小需求量N2,min时，电池要即换即充才能保证电动公交车的换电需求得到满足，换电站缺乏有序调控充电时间的调节裕度。当换电站备用电池组配置规模超过最小需求量N2,min，N2越大，换电站充电负荷的调节裕度越大。

2.2 换电站有序充电计划的优化模型

电动公交换电站是连接公交网络和配电网络的枢纽。公交车的日间运营特征，使得电动公交大规模接入后可能对城市配网负荷特性产生负面影响，增大电网峰荷需求，进一步拉大峰谷差。在满足电动公交运营需求的前提下，电网企业制定直接或间接激励措施激励电动公交换电站有序调控充电负荷，以减少对电网峰谷差的负面影响，对实现城市配电网络经济、安全运行具有重要意义。电动公交换电站运营商可响应电网企业降低峰谷差的激励措施，在满足公交车换电需求的前提下，有序控制换下来电池组的充电过程。

当换电站备用电池组配置规模超过最小需求量N2,min时，更换下来的电池的充电时间存在一定的调节裕度，换电站可以利用充电时间的调节裕度，选择合理的充电开始时刻，以实现对系统峰谷差d影响最小的充电计划控制目标，如式（11）

式中:psum(t)为电动公交换电站充电负荷接入区域的总负荷，即区域内其它负荷pbase(t)与换电站充电负荷p(t) 的总和，如式（12）

式中:充电负荷p(t)与换下来的电池的开始充电时刻和充电时长有关，计算如式（13）

式中:Pk,charge(t)为第k次换下来的电池组的充电功率曲线；pcharge为单一电池组充电功率。本文设电动公交电池充电过程为恒功率过程，在充电时长Tcharge内，充电功率不变。第k次换下来的电池组的开始充电时刻tc(k)是决策变量，其需满足式（15）的约束

2.3 蒙特卡洛模拟求解有序充电计划的优化模型

本文利用蒙特卡洛模拟求解上述有序充电计划的优化决策问题。该方法原理简单，易于实现，适用于小规模的优化求解［18］。具体步骤如下:

（1）在满足式（15）的约束下，随机生成初始的充电起始时刻tc()k。

（2）根据式（11）至式（14），将每次换下来电池所产生的充电负荷与系统的其它负荷叠加，形成换电站充电负荷接入区域的总负荷。

（3）计算区域总负荷的峰谷差，若峰谷差小于过程变量，则将此峰谷差值赋值给过程变量，并记录这组充电起始时刻数据，否则直接进行下一步仿真。

（4）判断是否达到设置的循环次数，若到达，则结束仿真，输出最小峰谷差以及优化决策的每块换下来电池的充电开始时刻。每次仿真中总循环次数设为1 000 000次，以保证仿真结果的准确度。

2.4 基于实时信息的日间滚动充电计划

根据式（4）预估次日各车的到站时间和到站SOC，采用2.2节中优化模型，形成日前充电计划。实际运行中，车辆的运行时间和SOC消耗与交通状况等很多因素有关，实际到站时间和到站SOC与预估值会有偏差。因此，有必要根据实测的车辆到站时间和到站SOC在日间滚动优化充电计划，动态修正日前充电计划控制充电机，换电站充电计划的滚动优化决策示意图如图3所示。

图3 换电站充电计划的滚动优化决策示意图

在实际运行日，当第k次电池的实际换电时间与预计时间不一致，则进行日间滚动优化。日间充电计划优化模型与日前充电计划优化模型一致，但需要根据实际发生数据修改相关参数。在日间滚动优化模型中，对于第k次更换下来的电池的充电时间，前第i( )i=1,…,k-1次更换下来的电池用其实际开始充电时间代入式（14）；，且根据第 k次更换下来的电池的际到站时间和到站SOC，调整约束条件式（15）中最早可以开始的充电时间t1(k)和最晚结束充电时间t2(k)。

求解日间滚动优化模型，决策出第k次换下来电池的充电开始时刻tc()k，修正日前充电计划，形成最新的日间充电计划。待第k+1次电池换电需求实际发生后，继续根据实际值与预计值是否存在偏差，判断是否滚动优化充电计划，如进行滚动优化，则对应修正第k+1次换下来电池的充电计划。

3 算例分析

以城市某条公交线路电气化为背景，研究线路采用电动公交后的充电负荷特性以及有序充电的调控策略。公交线路的运营时间为6:00～22:00，公交车行驶一圈的路程L是10 km，运行时间Trun平均为40 min，发车间隔Tgap为10 min，每次换电时间需求Tswap为10 min，电池SOC警戒水平SOCwarn取0.2，单位里程耗电量c取1.4 kWh/km，一组电池满电容量C为140 kWh。每组电池恒功率方式下充电功率pcharge为28 kW，每组电池每次充电时长为4 h。

3.1 换电需求分布

根据1.1节式（1），满足该线路公交调度计划的线路日运营电动公交车辆需求为5辆，采用1.2节图2所示的公交车状态转换时序分析模型，仿真一天的线路运营情况，一天内共有10次换电需求产生，具体产生时刻见表1。

表1 换电需求次数及其产生时刻表

3.2 充电负荷及其有序调控

满足上述换电需求，根据2.1节式（10）分析该条线路需要配置的备用电池组最小需求N2,min为5组，此时换电站的充电负荷为即换即充，缺乏有序调控裕度，图4展示了该模式下充电计划；图5展示了换电站配置备用电池组N2为6时，采用本文2.2节有序充电优化调控策略模式下的充电计划。

对比图4和图5可见，采用有序充电调控策略后，充电负荷分布更分散，部分充电负荷转移到夜间至清晨时间充电，且日间最大同时充电的电池组数量由图4中的5组电池下降为图5中的4组电池，降低了电网高峰负荷；尽管有序充电模式下夜间最大同时充电电池组数仍是5组，但该充电需求水平发生在夜间，起到了一定的填谷效应。

图4 即换即充模式下充电计划示意图

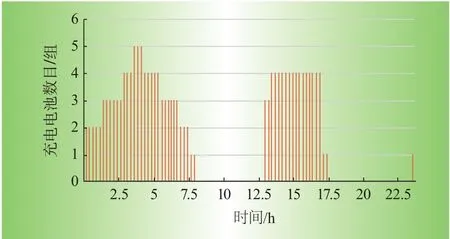
图5 有序充电模式下充电计划示意图

图6展示了叠加了该电动公交车充电负荷的10 kV馈线的负荷曲线变换情况，图6中蓝线为线路上接入的其它常规负荷曲线。若电动公交换电站采用即换即充的方式，其充电起始时刻取决于电池更换时刻，电池的充电计划与车辆调度计划硬关联，加剧了线路的高峰负荷和峰谷差，如图6中红线；若采用本文2.2节的有序充电策略，实现电池的充电计划与车辆调度计划间柔性关联，优化后的线路负荷曲线日间高峰负荷没有加剧，夜间有一定的填谷效应，如图6中绿线。

图6 有序充电调控前后线路负荷曲线对比

3.3 电池配置对充电负荷有序调控潜力的影响

换电站配置备用电池数量影响电池充电调度计划，仿真分析该条线路配置不同规模电池组数目时有序充电方式下的负荷曲线，结果如图7所示。由图7可见，伴随备用电池组数目的增加，电动汽车有序充电计划能更大力度地利用夜间负荷低谷时段充电，起到移峰填谷、改善负荷曲线的效果。

图7 不同电池数目配置下的线路负荷曲线

3.4 公交车调度发车间隔对充电负荷有序调控潜力的影响

首、末车运营时间和发车间隔是构成公交车调度计划的关键因素。传统非电动公交车的首末车运营时间和发车间隔一般参考线路的客流量情况和线路计划配车数等因素确定，可在一定范围内微调。首、末车运营时间的调整会导致电动公交的充电需求在时间轴上发生平移，但由于首、末车可调整的时间区间有限，与系统其它负荷错峰用电的潜力有限。电动公交的发车间隔是影响电池换电需求的产生次数和时刻分布的重要因素。故本文研究发车间隔参数调整对充电负荷的影响。上文算例中的运行线路其它参数不变，调整发车间隔时间，计算即换即充模式下此条公交线路日间充电负荷的峰值，结果如表2。

表2 发车间隔微调后充电峰荷

从表2中可以看出，发车间隔时间与充电负荷关联的敏感度具有非线性特征，如该条公交线路在7～10 min区间内微调发车间隔时间，会对最大充电负荷产生影响，最大同时充电的电池组数从8组降到5组；而在10～12 min区间内微调发车间隔时间，最大充电负荷没有变化。当发车间隔调整到13 min时，最大充电负荷降到4组电池同时充电。可见，对于发车间隔较小，且处于供电能力紧张区域的电动公交线路，合理规划发车间隔时间对降低高峰充电负荷需求具有重要意义。

4 结束语

本文考虑公交车调度计划的时序特征，同时计及换电站电池充电计划的调度需求，首先建立电动公交车状态转换时序分析流程，模拟电动公交换电需求的产生次数和时刻分布；其次考虑电动公交充电负荷接入电网对电网负荷特性的影响，建立计及电动公交车-电池联合调度的电动公交换电站有序充电决策模型，并采用蒙特卡洛模拟求解优化策略；最后结合算例分析电动公交电池充电计划优化安排和电池配置对其与电网削峰填谷能力的影响。算例仿真结果表明，计及电动公交车-电池联合调度的电池充电计划优化，有利于减少电动公交充电负荷接入对电网高峰负荷的冲击，增加低谷时段负荷需求。采用本文模型，可实现对电动公交充电负荷的精细化预测和有序调控，并分析电池配置规模和发车间隔时间对公交线路充电负荷有序调控潜力的影响，为电动公交线路设施配置和调度计划以及配电网规划运行提供决策支撑。后续，将进一步融合本文电动公交充电计划优化模型开展电动公交充换电设施的优化规划。

［1］ 杨泽宙.纯电动公交车充换电站经济效益研究［D］.北京:北京交通大学，2017.

［2］ 刘志鹏，文福拴，薛禹胜，等.电动汽车充电站的最优选址和定容［J］.电力系统自动化，2012，36（3）:54-59.

［3］ Wang G,Xu Z,Wen F,et al.Traffic ⁃Constrained Multiobjective Planning of Electric⁃Vehicle Charging Stations［J］.IEEE Transactions on Power Delivery,2013,28（4）:2 363-2 372.

［4］ DharmakeerthiCH,MithulananthanN,SahaTK.Modeling and planning of EV fast charging station in power grid［C］//Power and Energy Society General Meeting.IEEE,2012:1-8.

［5］ 高赐威，段天琪.电动汽车换电站定址分容研究［J］.电力需求侧管理，2015，17（1）:2-8

［6］ Worley O,Klabjan D.Optimization of battery charging and purchasing at electric vehicle battery swap stations［C］//Vehicle Power and Propulsion Conference.IEEE,2011:1-4.

［7］ Ip A,Fong S,Liu E.Optimization for allocating BEV recharging stations in urban areas by using hierarchical clustering［C］//International Conference on Advanced Information Management and Service.IEEE,2011:460-465.

［8］ 范子恺，俞豪君，朱俊澎，等.电力高峰时段电动汽车负荷优化调度［J］.电力需求侧管理，2014，16（5）:3-9.

［9］ 倪峰，赵明宇，陈良亮，等.电动汽车有序充电研究［J］.电力需求侧管理，2015,17（5）:16-19.

［10］ 张曦予，李秋硕，陶顺，等.电动公交车充电站功率需求影响因素分析及建模［J］.现代电力，2014，31（1）:28-33.

［11］ 李斌，刘畅，陈慧妙，等.基于混合整数规划的电动公交车快速充电站有序充电策略［J］.电网技术，2016，40（9）:2 623-2 629.

［12］ 苗淼，雷霞，何建平，等.考虑削峰填谷的电动公交换电站充电优化研究［J］.西华大学学报自然科学版，2015（4）:37-41.

［13］ 张帝，姜久春，张维戈，等.基于遗传算法的电动汽车换电站经济运行［J］.电网技术，2013，37（8）:2 101-2 107.

［14］ 钱斌，石东源，谢平平，等.电动公交车换电站—电池充电站优化规划［J］.电力系统自动化，2014（2）:64-69.

［15］ 金杰，金艳.具有填谷功能的太阳能发电站-公交车换电站的研究［J］.智能电网，2016，4（1）:50-53.

［16］ 朱鹰屏，韩新莹，刘世立，等.基于改进双中心粒子群算法的电动公交车运营数量优化策略研究［J］.电力系统保护与控制，2017，45（8）:126-131.

［17］ 张维戈.纯电动公交车换电站优化设计和经济运行研究［D］.北京:北京交通大学，2013.

［18］ 苗世洪，徐浩，钱甜甜，等.扩展时间尺度下的电动汽车有序充电策略［J］.中国电机工程学报，2015，35（23）:5 959-5 967.