基于分形理论的水下地形生成∗
潘竹炉
1 引言
地球表面上71%的区域是海洋,海洋把世界联系到一起,然而到目前为止,人类已探测的海底只有5%,还有95%的海底是未知的[1]。海洋不仅是生命的源泉,提供了人类赖以生存的物质和空间,还蕴含丰富的生物、化学、矿产等资源。随着人类活动空间的扩展,航海早已不局限于海面上,潜艇、水下机器人等航海新设备急切需要水下三维空间地形图。二维电子海图只能用水深和等深线来描述水下的地形地貌,有表述不直观、信息不全等问题,不利于海底地形分析。利用传统的二维矢量电子海图提供的水深数据、等深线和海岸线等信息构建水下DEM,将使水下空间可观测维数大大增加。三维海底地形可视化系统操作更简便、表达更直观、逼真性更强、信息量更大,更有利于人的接受、感知和理解。
2 数字高程模型
数字高程模型(DEM)一般来说是将离散、不规则的原始采样高程值使用某些数学手段(例如过采样、拟合、插值等)重建出相似曲面来逼近原始的地表。常见的DEM模型根据数据结构的不同主要分为规则格网DEM(如图1(a))和不规则三角网DEM(如图1(b))。规则格网数据结构冗余较多,但是拓扑关系较好,数据存储简单;不规则三角网有较好的数学结构,数据冗余少,但拓扑关系较差,数据存储复杂[2]。
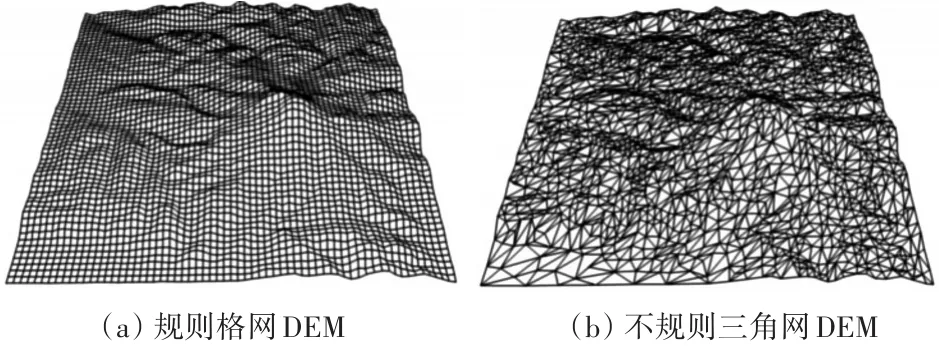
图1 常见数字高程模型
数字高程模型的平滑内插是基于海底地形的过渡平滑趋势构建三维海底地形的,通过二维海图提供的离散水深点的水深,估计拟合离散点之间的水深,从而构建出完整的水下地形。由海底的过度平滑趋势可知,距离越近的点,相关度越高。由图2所示,按内插点的区域可分为分块内插、逐点内插和整体内插。但是考虑到数据量的问题,一般采用逐点内插,目前,较简单的算法有特定区域的圆、TIN三角网插值、基于VoronoiCells的自然临近点插值[3](例如Sibson插值、Laplace插值)、基于数据融合的插值算法[4]。
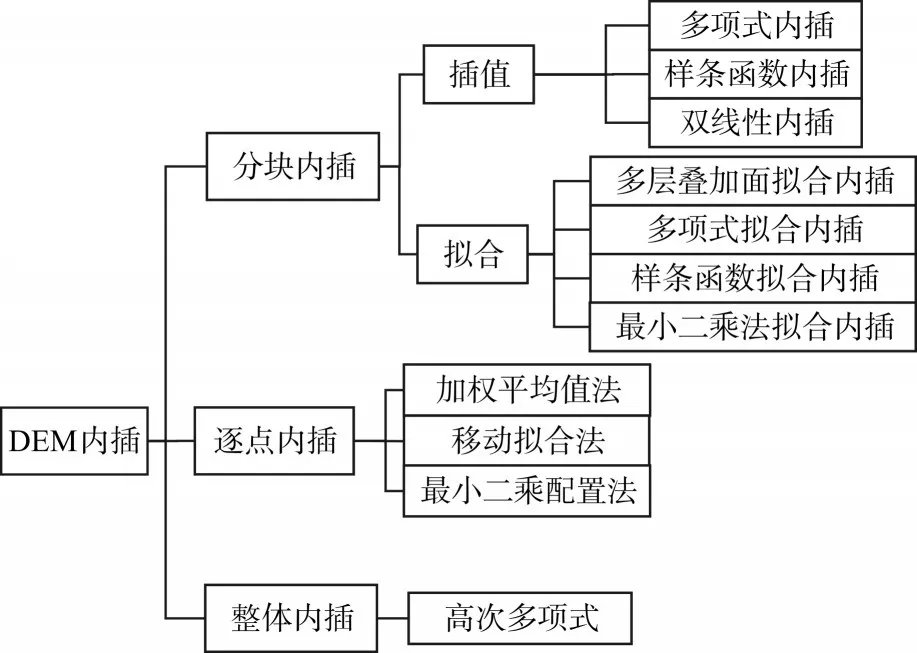
图2 DEM平滑内插分类
3 分形内插算法构建DEM
分形理论隶属于非线性科学,在生物、地球科学、材料物理等领域都有着很广泛的应用[5]。分形理论萌芽于19世纪60年代,于20世纪七、八十年代正式演变为一门独立的学科,分形插值是分形理论的一个重要应用。分形插值主要应用了分形的自相似原理,利用迭代算法由原始特征插值出局部细小特征。分形能表达出自然界中许多非线性现象,使用分形插值理论构建地表或许最能逼近自然界真实地形[6]。
3.1 分形理论简介
分形理论(Fractal Theory)是一门以不规则几何形态为研究对象的新理论、新学科。分形对象在自然界是普遍存在的,粗糙不平的地表、弯弯曲曲的海岸线、绵延不绝的山脉、袅袅的炊烟、枝繁叶茂的数木、漫天飞舞的雪花等都是分形。
Mandelbrot因为提出了“英国的海岸线有多长”的问题有了分形思想萌芽的故事几乎成为佳话被广为流传。大量经典的分形是自相似的,这种分形的局部和整体具有一定比例的几何相似性,如Sierpinski垫片(图3(a)),Koch曲线(图3(b))。自相似集的生成元中,每一个压缩映射都把它变换为一个小拷贝,它在不同方向上的压缩比是相同的。多次迭代过程最终输出图形与输入变得无关,真正决定最终输出的是反馈机器中的数学变换,Barns⁃ley等把这种数学变换称为迭代函数系(Iterated Functional System),简写为IFS。
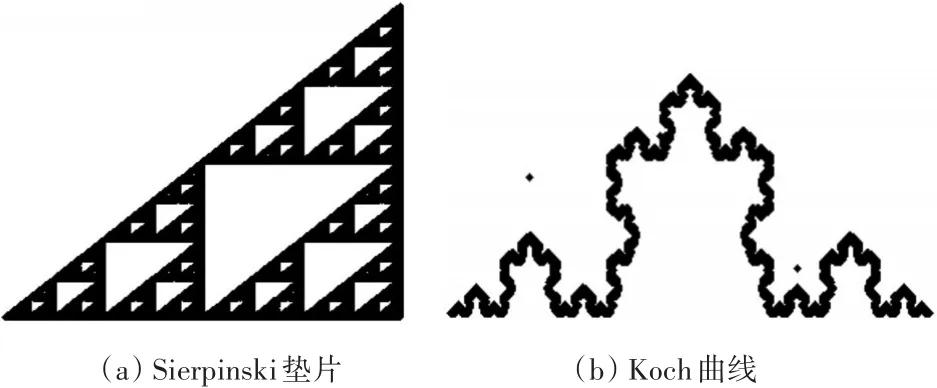
图3 常见的分形图形
3.2 分形插值算法
分形插值由Barnsley在IFS的基础上归纳推导出来[7]。它是分形理论的一个重要应用。自Euclid创立几何以来,人们提出了各种插值算法来描述几何体。然而对于现实世界的大量离散数据,除了直到20世纪60年代提出的样条函数插值[8],几乎没有任何方法能完美克服几何体的低阶全局光滑问题。可见数学插值更偏爱“光滑”,“平滑”等字眼。分形插值函数[9]利用大自然中广泛存在的精细自相似结构特征来拟合滚动性强的曲线,为解决几何体的低阶全局光滑问题开辟了新的领域。
3.2.1 三维IFS分形插值算法推导
两个维度的数据集合 I=[a,b],J=[c,d];设平面点集 D=I×J={(x,y)∶x∈I,y∈J} ,以 △x,△y 为步长,将D按M×N格网化:
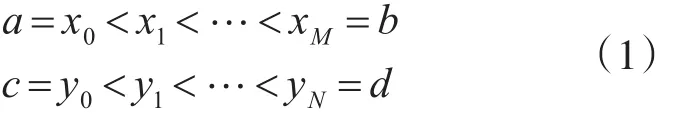
设(xm,yn){m=0,1,…,M;n=0,1,…,N}点处的高程数据为zm,n,我们的目的是构造二元分形插值函数 f∶D→R ,使
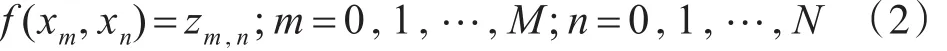
设满足上式的X方向和Y方向仿射变换为

且满足边界条件:
由式(3)和(4)可解得
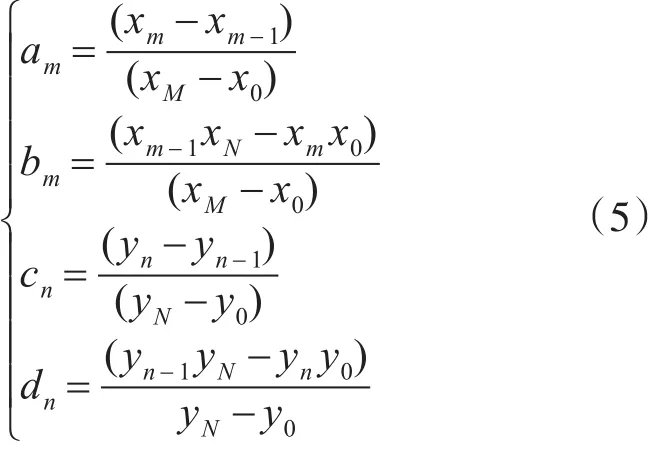
则可得平面点集x和y方向上得仿射变换为
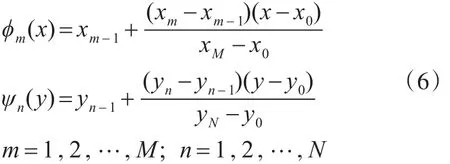
设高程z方向的仿射变换为
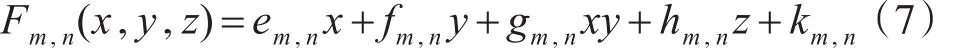
式中hm,n为高程z方向上的压缩倍率,它是决定分形插值后曲面的粗糙起伏程度的自由参数,需满足 0≤hm,n<1(否则IFS不收敛),一般称它为垂直比例因子。
而且可得边界条件:
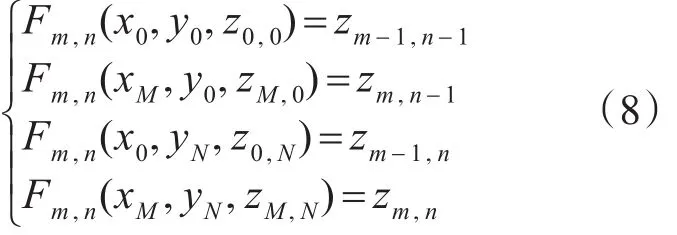
联立式(7)和(8)可得
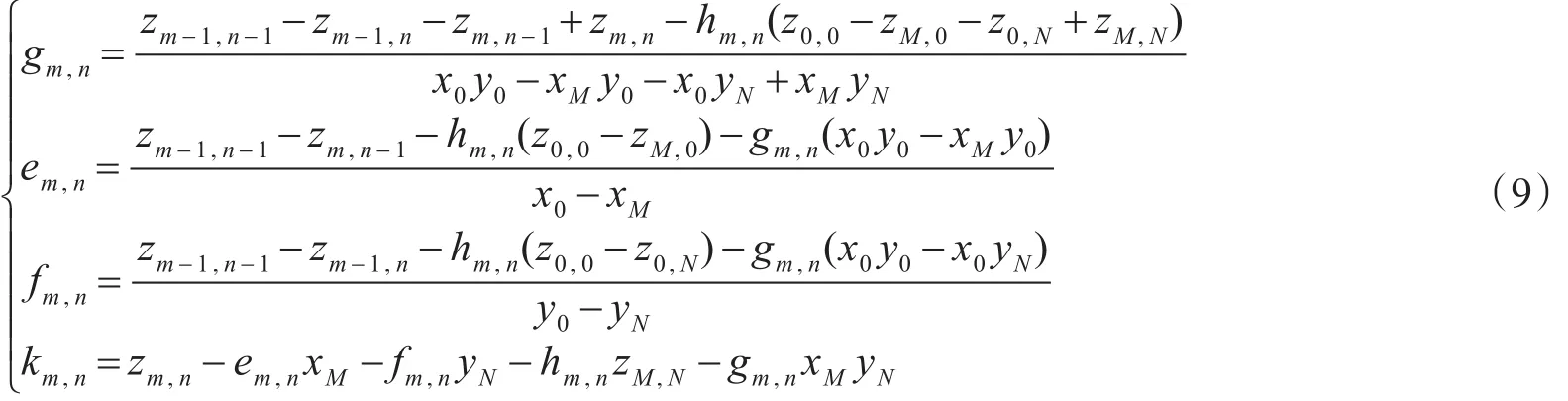
令 Wm,n(x,y,z)=(ϕm(x),ψn(y),Fm,n(x,y,z));(m=1,2,…,M;n=1,2,…,N),那么就定义了一个迭代函数系统。 Fm,n(x,y,z)为分形插值函数fm,n(x,y)的隐函数。
3.2.2 分形插值曲面的计算步骤
根据上面推导的公式,分形插值曲面的算法步骤如下:
1)输入待插值的格网化后的点云(xm,yn,zm,n);m=0,1,2,…,M;n=0,1,2,…,N ;
2)输入自由参数 hm,n;
3)根据式(9)计算参数 gm,n,em,n,fm,n,km,n;
4)根 据 式(6)和(7)计 算 :ϕm(xi),ψn(yj),Fm,n(xi,yj,zi,j) ,m=1,2,…,M ;n=1,2,…,N ;i=0,1,…,M ;j=0,1,…N ;
5)经过步骤4)原来的 (M+1)×(N+1)格网变成((M-1)2+1)×((N-1)2+1)格网。数据量大大增加,这就是一次分形插值曲面。若不够密集,可以继续进行二次迭代。
4 三维海底地形的仿真实现
为了验证测试算法的插值效果,选取一个上海长兴岛附近的二维电子海图作为数据源,如图4所示,图中左边陆地是横沙岛,右边是长兴岛,上面的黑点就是离散点的水深位置分布。

图4 离散水深点在谷歌地球上的分布
为了方便构建DEM,在陆地部分加入SRTM[10]高程数据,然后将补充数据后的平面离散点集使用平滑内插算法—移动拟合法生成的DEM如图5所示。
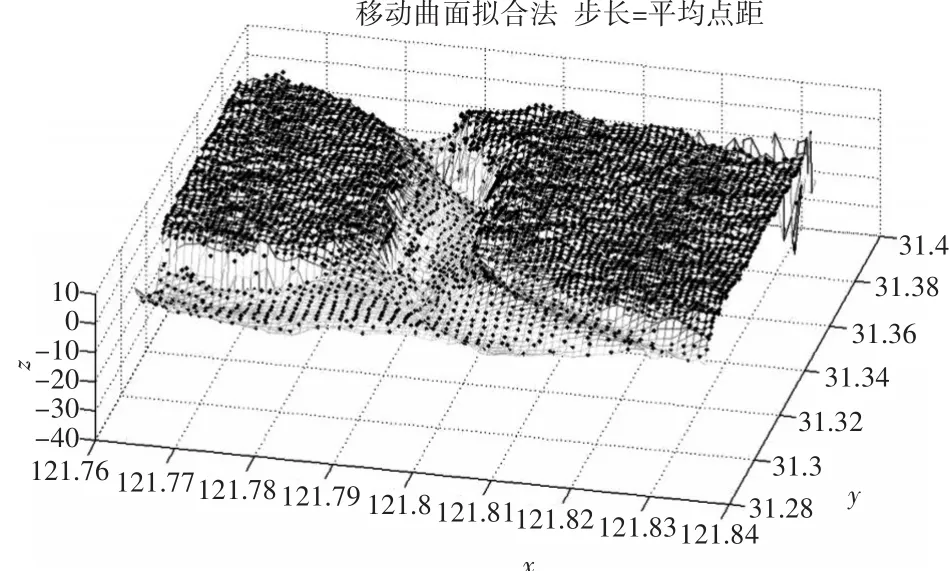
图5 平滑内插算法输出的DEM
原始二维海图离散的水深数据共有1790组(以一个高程点数据为一组),以平均点距的1.62倍格网化成29×24格网化,使用Matlab实现分形插值曲面算法得到785×530的格网数据,如图6所示,选取的自由参数为0.3,此时由于自由参数比较大,所以地形起伏比较大,但是基本上保持了实际的陆地海洋边界,如果自由参数选的足够小,则分形后的地形变得很光滑,也就退化为传统插值算法。
由图5和图6可以看出,分形插值前后的主要变化是
1)离散数据集比较小的情况下,数据量大大增加,高程点变得更加密集;
2)分形插值后局部和整体具有一定比例的几何相似性,这就是分形的自相似性。
选取自由参数为0.1的分形插值后的三维高程数据,采用DEM可视化技术,导入MultiGen Creator[11]地形建模工具生成的视图如图7所示。
5 结语
三维海底地形图在在军事仿真、水下作业、游戏开发和虚拟现实等方面都有十分广阔的应用前景。本文综合利用离散的水深信息构建数字高程模型,推导了数字高程模型的三维分形内插算法,并通过Matlab建模比较了传统平滑内插算法和分形插值算法,为三维水下地形图提供了一种行之有效的实现方法。
[1]http://www.noaa.gov/ocean.html[EB/OL].
[2]沈海峰,李庆阳.电子海图高程数据的离散化研究[C]//广州:第四届广东海事高级论坛论文集,2012:94-97.
[3]申浩,田峰敏,赵玉新.基于VoronoiCells插值的三维海底地形图生成方法[J].系统仿真学报,2006,18(2):444-446,450.
[4]赵凯,胡大斌,肖建波.基于数据融合的DEM插值与可视化[J].计算机仿真,2012,29(7):144-146,213.
[5]朱华,姬翠翠.分形理论及其应用[M].北京:科学出版社,2011.1,27-47.
[6]邱秋香.三维海底地形仿真技术的研究与实现[D].哈尔滨:哈尔滨工程大学,2011:9.
[7]卢福丹,陈元枝,蔡续.三维海底地形仿真的研究[J].计算机应用与软件,2014,31(1):77-80.
[8]陈颙,陈凌.分形几何学[M].北京:地震出版社,2005:5-6,35-44.
[9]孙洪泉.分形几何与分形插值[M].北京:科学出版社,2011:99-219.
[10]http://en.wikipedia.org/wiki/SRTM[EB/OL].
[11]王乘,周均清,李利军.Creator可视化仿真建模技术[M].武汉:华中科技大学出版社,2005:261,356.

