基于TensorFlow深度学习框架的卷积神经网络研究

袁文翠， 孔雪

(东北石油大学 计算机与信息技术学院，大庆 163318)

0 引言

众所周知，随着人们对智能化需求的提高，人工智能将是未来发展的大方向。从企业到国家甚至全球对人工智能领域都非常重视，深度学习则是人工智能领域的一个重要分支。本文针对深度学习中的卷积神经网进行了研究，并在手写数字数据集的识别上进行了应用实验。主要工作包括两方面：一是构建卷积神经网络对手写数字数据集进行识别，运用交叉熵损失函数去代替传统二次代价函数，并通过使用Relu激活函数来防止梯度消失来增加学习的速率，提高模型的准确率；二是在TensorFlow[1]中利用改进后的卷积神经网对手写数字数据集的分类结果进行直观展示。TensorFlow是谷歌在深刻总结其前身 DistBelief 的经验教训上形成的目前比较流行的深度学习框架，与其他框架相比，具有可以在不同的计算机上运行，以及高度灵活性、可移植性、自动求微分等特征。

1 CNN卷积神经网络基本结构

在神经网络中，BP神经网络的应用是十分广泛的，但是其有很多的缺点，例如：权值太多，计算量太大，网络结构复杂，容易造成过拟合等现象的发生。为了解决这些问题，在1962年哈佛医学院神经生理学家Hubel和Wiesel[2]通过对猫视觉皮层细胞的研究，提出了感受野的概念，1984年日本学者Fukushima基于感受野概念提出的神经认知机neocognitron[3]可以看作是卷积神经络的第一个实现网络，也是感受野概念在人工神经网络领域的首次应用。

卷积神经网络[4]是一种特殊的深层的神经网络模型，它的特殊性体现在两个方面，一方面它的神经元间的连接是非全连接的，另一方面同一层中某些神经元之间的连接的权重是共享的(即相同的)。它的非全连接和权值共享的网络结构使之更类似于生物神经网络，降低了网络模型的复杂度，减少了权值的数量。很好的解决了传统神经网络权值过多计算量过大的问题。

CNN的基本结构包括两种特殊的神经元层，其一为卷积层，每个神经元的输入与前一层的局部相连，并提取该局部的特征；其二是池化层，用来求局部敏感性与二次特征提取的计算层。这种两次特征提取结构减少了特征分辨率，减少了需要优化的参数数目。CNN网络结构，如图1所示。

2 对CNN卷积神经网络进行优化

2.1 对目标函数进行优化

每一个算法都有一个目标函数(objective function)，算法就是让这个目标函数达到最优。首先我们看一下传统的二次代价函数(quadratic cost)：

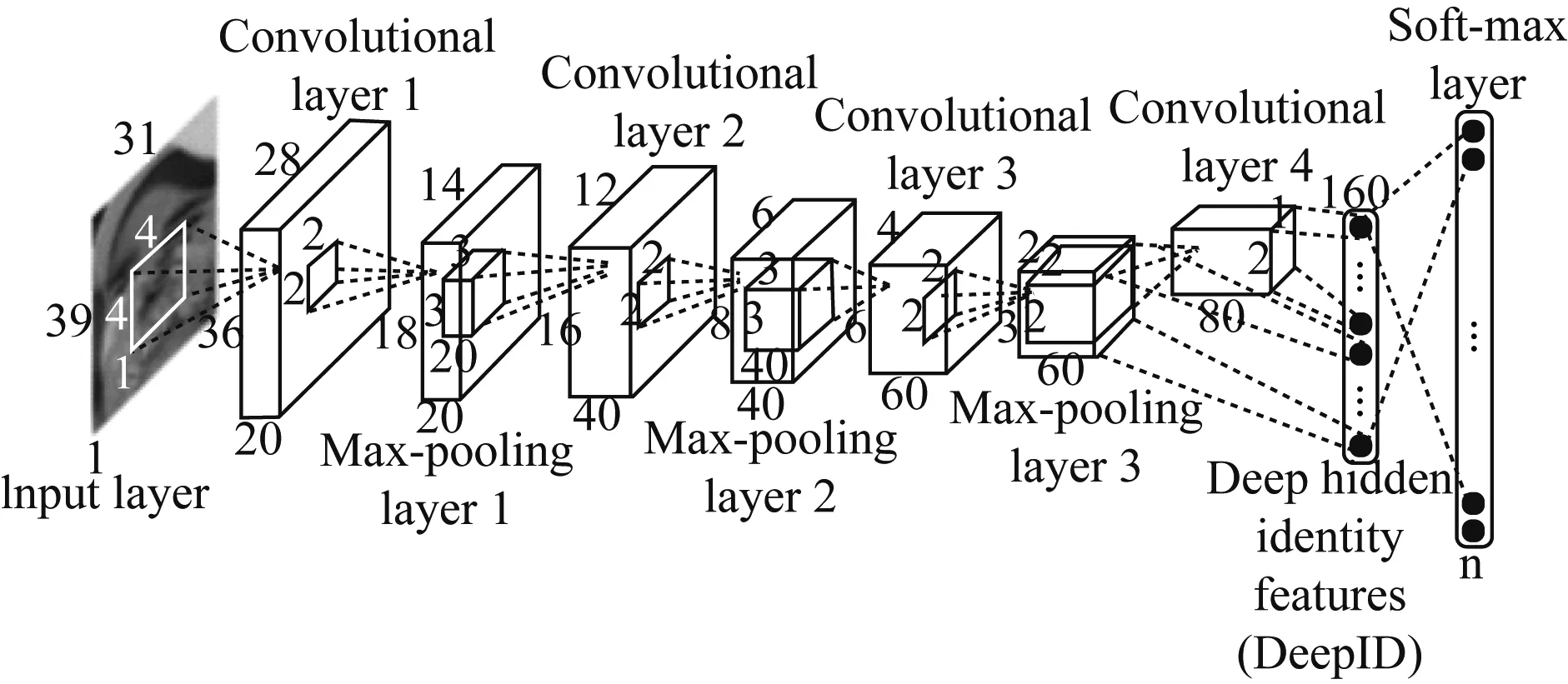
图1 CNN卷积网络结构图

其中，C表示目标函数，x表示样本，y表示实际值，a表示输出值，n表示样本的总数。在公式中y(x)-a(x)就是真实值与输出值得差，也就是误差值。所以我们的目标就是使误差最小化也就是目标函数最小化，为简单起见 ，同样以一个样本为例进行说明，此时二次代价函数为：

假如我们使用梯度下降法(Gradient descent)[5]来调整权值参数的大小，权值w和偏置b的梯度推导如式(1)、(2)。

(1)

(2)

其中，z表示神经元的输入，σ表示激活函数。w和b的梯度跟激活函数的梯度成正比，激活函数的梯度越大，w和b的大小调整得越快，训练收敛得就越快。假设我们的激活函数是Sigmoid函数,如图2所示。

图2 sigmoid函数

假设我们的目标是收敛到1，A点为0.82,距离目标比较远，梯度比较大，权值调整的比较快，学习速率快，而B点为0.98距离目标比较近，梯度较小，权值调整较慢，学习速率较低，以上情况符合我们的预期，距离目标越远则学习速率越快，距离目标较近的时候降低学习速率，可以避免学习速率过快而找不到最低点。

反之如果我们的目标是0，则所达到的结果远离我们的预期，所以我们将改变一下原有的二次代价函数，使权值和偏置值的调整与σ′(z)无关，这样就解决了上述问题。在本文中我们将用交叉熵代价函数去代替二次代价函数。首先我们先看一下交叉熵代价函数的推导过程：

由公式(2)可知为了消除σ′(z)，想得到一个代价函数使得式(3)。

(3)

由公式(3)即可推出式(4)。

(4)

对公式(4)两侧求微分可得交叉熵代价函数：

其中，C表示目标函数，x表示样本，y表示实际值，a表示输出值，n表示样本的总数。在这里我们还使用梯度下降法来调整权值参数的大小，权值w和偏置b的梯度推导如下：

由以上推导公式可以看出权值和偏置值的调整与σ′(z)无关，另外，梯度公式中的σ(z)-y表示输出值与实际值的误差。所以当误差越大时，梯度就越大，参数w和b的调整就越快，训练的速度也就越快。很好的解决了激活函数梯度的变化对权值更新速率的影响。

2.2 对激活函数进行改进

2.2.1 sigmoid激活函数结构分析

激活函数是神经网络中的一个重要组成部分，通过对神经网络的输入进行函数变换，得到适当的输出，通常情况下激活函数为线性表达能力较差的神经网络注入非线性因素，使数据能够在非线性的情况下可分，也可以将数据进行稀疏表达，更加高效的进行数据的处理。而可以提高学习速率。

传统神经网络中最常用的两个激活函数，Sigmoid系(Logistic-Sigmoid、Tanh-Sigmoid)被视为神经网络的核心所在。传统激活函数图像，如图3所示。(摘于AlexNet的论文Deep Sparse Rectifier Neural Networks)。

图3 sigmoid/tanh函数

一般我们优化参数时会用到误差反向传播算法，即要对激活函数求导，得到sigmoid函数的瞬时变化率，其导数表达式为：

φ′(x)=φ(x)(1-φ(x))

导数图像，如图4所示。

图4 sigmoid/ sigmoid’函数

由图可知，导数从0开始很快就又趋近于0了，易造成“梯度消失”现象,使学习停滞。为解决这一问题我们将提出Relu激活函数[7]来代替传统的sigmoid系函数。

2.2.2 Relu激活函数[5]结构分析

Relu的函数式：

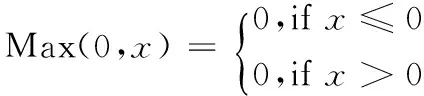
Relu函数图像，如图5所示。

图5 Relu函数

由图5可以看出，Relu会使一部分神经元的输出为0，这样就造成了网络的稀疏性，并且减少了参数的相互依存关系，缓解了过拟合问题的发生，并且发现ReLu更容易学习优化。因为其分段线性性质，导致其前传，后传，求导都是分段线性。而传统的Sigmoid函数，由于两端饱和，在传播过程中容易丢弃信息。所以本文将选用Relu激活函数和交叉熵代价函数进行试验去提高实验的准确率。

3 实验验证

3.1 运用手写识别数据集进行实验

本实验运行的环境是anaconda3中的juypter notebook。由于每次训练后模型都会更新权值和偏向，从而提高准确率，在进行20次实验后模型的准确率提高幅度几乎为零，所以本实验将进行20次训练。

首先运用传统简单的三层神经网络进行实验，每个训练批次的大小是100张图片，训练20次，没有进行目标函数和激活函数的改进，试验结果，如图6所示。

由实验结果可以看出，在进行10次训练后模型的准确率才达到90%以上，说明用简单的传统神经网络进行训练得到的模型学习速率慢，准确率低。由此我们将进行改进，将传统的神经网络改为CNN卷积神经网络进行试验，看是否可以提高学习速率和准确率，如图6所示。

图6 第一次实验结果图

在这次实验中，我们将构建一个有两层卷积层和两层池化层的卷积神经网络，没有对网络中的目标函数和激励函数进行改进，得到实验结果，如图7所示。

图7 第二次实验结果图

运用CNN卷积神经网络进行模型训练后，在第一次模型训练后结果就已经达到90%以上，基本达到普通神经网络的最终训练结果，并且准确率也有了大幅度的提升。

在这次实验中我们将在上次实验的基础上对模型的目标函数和激励函数进行改进，看看是否可以提升模型的准确率，实验结果，如图8所示。

图8 第三次实验结果图

由实验结果可以看出，在第二次训练后模型的准确率已经达到了97%以上，解决了学习速率低的问题，并且在模型的准确率方面也有所提升，所以通过以上三次实验可以论证本文提出的方法确实可以提高模型的准确率。

3.2 运用TensorBoard进行模型可视化

TensorBoard是TensorFlow内嵌的可视化组件，可以通过读取事件日志进行相关摘要信息的可视化展示。下面我们将对模型精准度和模型分类效果进行可视化，如图9所示。

图9中紫色线是测试集的精准率走势，橘色线是训练集的走势，我们很容易的可以看出，测试集和训练集的走势基本一致，可以判断模型没有发生过拟合[6]的现象，如图10所示。

图10将0到9十个数字行进分类训练，并且以不同的颜色进行标记，图10是模型训练1 000轮后显示出来的效果图。通过此图可以很直观的看到模型的分类效果。

图10 分类效果图

4 总结

目前深度学习已经被广泛应用于学术界和工业界，但在深度学习的多种神经网络中，卷积神经神经网络无论是在速率，还是在准确率方面表现都是最为出色的，本文提出一种对卷积神经网络进行优化的两种方式，并且通过实验验证得到了具有较高识别精度的模型，对构建更复杂的卷积神经网络具有一定的参考意义。

[1] 章敏敏,徐和平,王晓洁,周梦昀,洪淑月. 谷歌TensorFlow机器学习框架及应用[J/OL]. 微型机与应用,2017,36(10):58-60.

[2] HUBEL D H, WIESEL T N. Receptive fields，binocular interaction，and functional architecture in the cat's visual cortex [J].Journal of Physiology,1962,160(1):106-154．

[3] FUKUSHIMA K. Neocognitron: a self-organizing neural network model for a mechanism of pattern recognition unaffected by shift in position [J]. Biological Cybernetics,1980,36(4):193-202．

[4] 李彦冬,郝宗波,雷航. 卷积神经网络研究综述[J]. 计算机应用,2016,36(9):2508-2515.

[5] Dmitry Yarotsky. Error bounds for approximations with deep ReLU networks[J]. Neural Networks,2017.

[6] Murphy K P. Machine Learning: A Probabilistic Perspective[M]. Cambridge， MA: MIT Press,2012: 82-92．