堆垛机神经网络PID控制系统研究

，

(陕西国防工业职业技术学院，陕西 西安 710300)

0 引言

一个完整的自动化立体仓库系统，应该是在人机互动下共同来完成相应的操作过程，主要是采用计算机控制来实现的，通过对计算机输入执行指令，来定位仓库。对于有些仓库系统由于货物的特殊原因，不能进行现场操作，也可以通过计算机实现远程操作，并且可以对货物的运行情况进行实时监控，完全保证了货物的精确定位。目前，工业生产型立体化仓库已从机电控制的高架仓库，发展到以智能化、集成化和信息化为特征的第5代自动化立体仓库阶段[1]。这样对电机的控制要求就显得十分重要。

传统PI控制在对控制对象模型要求不高的情况下，能够很好地对系统进行调节与控制，可靠性高，易于实现，目前仍被广泛用于各种控制任务中。但在堆垛机控制系统中，要达到给定的控制要求，堆垛机需具有一定的稳定性和良好的系统抗干扰能力，同时对机械环和加速度的响应能力要求较高，故传统的PID控制难以胜任[2]。引入神经网络控制，利用其自组织、自学习能力可以有效地对堆垛机施加控制。在此，提出了一种基于BP神经网络PID(BP-PID)与常规PI复合的控制方法，根据设置的误差限来实现控制策略的切换，这样结合两者控制上的优点解决了堆垛机系统控制上的难点。

1 堆垛机控制过程

堆垛机的控制过程是在x，y，z轴3个方向下的三维空间内完成的，如图1所示。

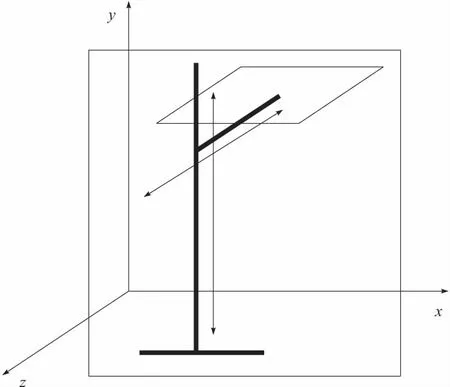
图1 堆垛机控制系统三维空间

其中，堆垛机水平行走机构，主要完成在立体仓库铺设的轨道上做水平运动，把这个方向上的运动定义为x轴运动方向；堆垛机的提升机构主要完成在机体立柱上的运动，相对于整个机体在垂直平面内做上升或下降运动，把这个方向上的运动定义为y轴运动方向；堆垛机的货叉机构完成在载货台上的伸缩运动，把这个方向上的运动定义为z轴运动方向[3-4]。

这样，对堆垛机的控制过程就转化为对x，y，z轴上3个电机的控制。为了达到快速、准确地定位货仓位置，根据货仓位置信息的距离，通过数据处理，在转速控制上采取了先加速再减速或先加速再匀速最后再减速的控制过程[5-6]，如图2所示。

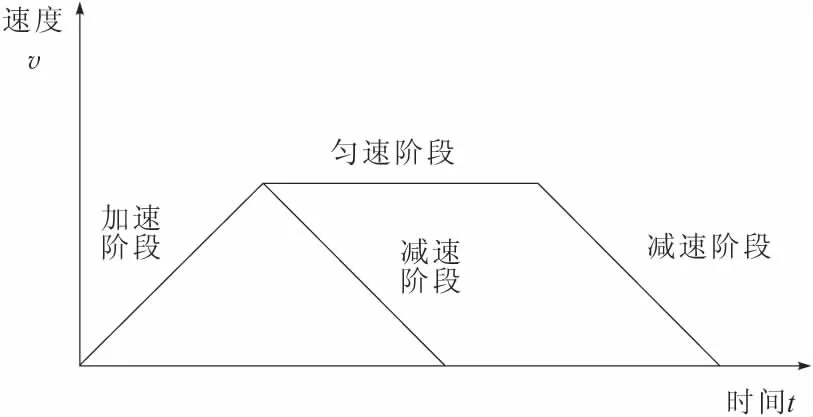
图2 堆垛机速度控制过程

根据设置的速度误差限，控制器将在BP-PID控制与PI控制之间进行切换，实现转矩与磁链稳定、快速的转换，提高了转速的跟随性与抗干扰性。

2 堆垛机控制系统模型

堆垛机控制系统具有非线性、强耦合和多变量的特性，要获得较高的动静态性能，必须从其系统模型出发，分析转矩和磁链的控制规律。Park的输入整形控制法稳定性不佳[7]。文中通过坐标变换，在按转子磁链定向的坐标系中得到直流电动机模型；通过直流电动机模型的控制方法，得到磁链与转矩的控制规律；最后将转子磁链定向坐标系中得到的控制量反变化到三相坐标系下对应的控制量，以实施闭环控制[8]。

静止正交坐标系与按转子磁链定向的同步旋转正交坐标系如图3所示。其中，αβ为静止正交坐标系，mt为按转子磁链定向的同步旋转正交坐标系，即旋转正交dq坐标系中的d轴与转子磁链矢量重合的状态。当m轴与转子磁链矢量重合时，有：

图3 按转子磁链定向同步旋转坐标

(1)

ψrt=ψrq=0

(2)

为了使m轴与转子磁链矢量始终重合，还必须使：

(3)

由电机的理论知识可知，以ω-is-ψr为状态变量的状态方程为：

关于建筑业的绿色化发展，主要存在以下几个问题，对我国绿色建筑的发展造成了障碍，同时也造成了能源浪费，不利于企业经济效益的发展。

(4)

将式(1)、式(2)、式(3)代入式(4)中,得到mt坐标系中的状态方程为：

(5)

这样从式(5)中导出mt坐标系的旋转角速度为：

(6)

mt坐标系旋转角速度与转子转速之差为转差角频率，即

(7)

将式(1)、式(2)代入转矩方程式，得到mt坐标系中的电磁转矩表达式为：

ψr

(8)

这样，定子电流被分解为励磁分量和转矩分量，励磁仅由励磁电流分量ism产生，转矩正比于磁链和转矩电流分量，实现了定子电流2个分量的解耦。

3 堆垛机BP-PID控制

堆垛机控制系统要具有稳定、快速、抗干扰性，其中调节器在里面起到了关键作用。模糊控制由于缺乏系统性，无法定义控制目标[9]，文中设计了一种BP-PID与常规PI复合控制的调节器，结合两者的优点实现了对堆垛机控制系统的有效控制。其中BP神经网络PID控制结构如图4所示。

图4 BP-PID控制系统结构

由图4可以看出，BP-PID控制结构是由BP神经网络和PID控制器2部分组成的。BP神经网络根据系统输入误差信号e(k)和PID控制器输出信号u(k)，在线调整PID控制参数KP，KI，KD；PID控制器根据系统状态直接对系统进行闭环控制，其PID参数受控于BP神经网络，通过神经网络自学习、自组织能力实现系统参数最优化控制。其中，BP神经网络是输入层、隐含层和输出层3层神经元的互联体。每次BP网络学习过程经过了正向传输和反向传播2个部分，输入信号经过3层神经元后输出PID控制参数，通过PID控制器对被控对象施加控制，被控对象输出参数与目标信号进行比较，得到误差值和系统的运行状态。最终通过误差反向传播对各层神经元权系数进行修正，使得输出参数无限逼近于目标值[9-10]。

本文结合BP-PID控制与常规PI控制两者的优点，采用BP-PID与PI并联复合的控制方法，如图5所示，通过输入误差与设定误差限的比较进行控制切换。当速度误差大于设定值时，选取BP-PID控制策略，利用BP神经网络自学习能力，将误差快速减小到设定误差值以下；当速度误差小于设定值时，选取PI控制策略，利用其算法简单、运算速度快等特点，满足堆垛机系统实时性要求。在常规PI控制策略中，采用了PI变参数法，根据负载转矩误差限来实时调整PI参数，将系统误差消除在萌芽状态，提高了系统稳定性和抗干扰性。

图5 BP-PID与PI并联复合结构

4 堆垛机MATLAB仿真模型

在MATLAB/Simulink环境中，对堆垛机控制系统进行了仿真研究。为了便于分析与处理，将交流电机模块、驱动模块和速度检测模块看成一阶惯性环节。其中，交流电机输入频率与输出稳态转速比值KD=27；电机时间常数TD=0.19 s；转速反馈系数α=0.004 1;测速仪时间常数TC=0.006 s。

其中，用于BP神经网络PID控制的仿真模型如图6所示。

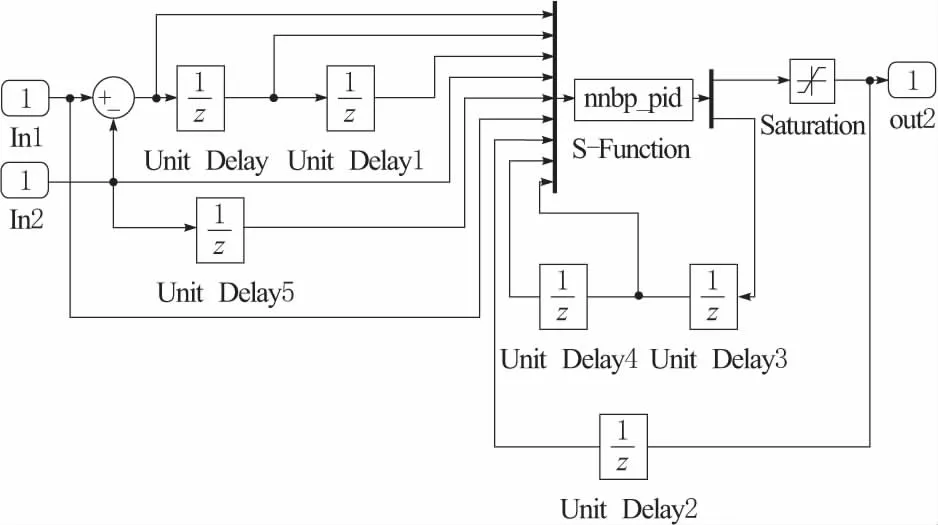
图6 BP-PID控制系统仿真模型

BP-PID的学习速率η=0.25，α=0.05，转速切换值为50 r/min。BP-PID控制进行的主要运算由Simulink中的S-function实现，采用输入层4个节点，隐含层5个节点，输出层3个节点的网络结构。

5 仿真结果与分析

对堆垛机的启动、停车和负载变化这3种工况下的运行状态进行了仿真，其中虚线为PI控制下的响应曲线，实线为PI与BP-PID复合控制下的响应曲线，仿真时间为10 s，仿真步长设为0.05。

堆垛机启动状态下的响应曲线如图7所示。由图7可知，采用PI控制调节时间约为6.5 s，在8.5 s达到稳定状态；采用PI与BP-PID控制调节时间为4.5 s，在6 s达到稳定状态，响应速度优于PI控制，且具有较小的超调量。

图7 启动响应对比

负载变化时，PI控制与复合控制的响应曲线对比如图8所示。当系统达到稳定后，在15 s时改变负载。由图8可知，当负载变化时，BP-PID与PI复合控制能够让系统快速进入新的平衡状态，且波动较小；而PI控制调节时间长，且有一定的波动量。

图8 负载变化响应对比

堆垛机系统停车时的响应曲线对比如图9所示。由图9可知，在系统稳定状态下，20 s时开始制动减速，采用PI控制在28 s时完全停车；采用复合控制在26 s时完全停车，系统响应速度快，调节时间短。

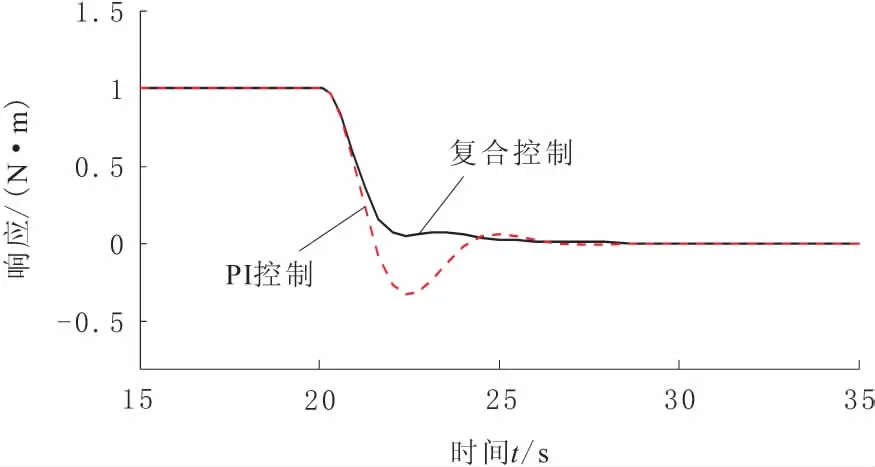
图9 停车响应对比

6 结束语

通过BP神经网络PID与传统PI控制相结合的控制方法，两者取长补短，较好地解决了堆垛机控制系统中存在的系统参数变动和负载扰动等问题。通过速度误差限切换控制策略，在传统PI控制时，采用了PI变参数法，对速度误差进行快速预判和消除。仿真结果表明，BP-PID与BP复合的控制方法具有较快的调节速度，且波动量小，系统动静态性能良好。

[1] 蔡安江，应嘉奇，王坚，等.分散式立体仓库堆垛机调度模型[J].计算机集成制造系统，2016，22(3)：793-799.

[2] 王雪，蔡安江，应嘉奇.基于模糊PID的堆垛机控制系统研究[J].机械设计与制造,2017(5)：17-20.

[3] 金琦淳，胡元，崔吉.自动化立体仓库中堆垛机的设计[J].制造业自动化，2012，34(8)：116-118.

[4] 张晓东，曹毅，李秀娟.立体仓库巷道堆垛机控制系统设计[J].自动化仪表，2013，34(5)：46-48.

[5] 闫兴华，葛影，马顺杰.堆垛机光电开关系统的优化设计[J].起重运输机械，2016(5)：54-56.

[6] 鲁春强.基于堆垛机行走速度自适应参数模型的算法研究[J].物流技术，2012，31(12)：359-361，453.

[7] Park B J, Hong K S, Huh C D. Time-efficient input shaping control of container crane systems[C]//Proceedings of IEEE International Conference on Control Applications,2000：80-85.

[8] Abdel-Rahman E M, Nayfeh A H, Masoud Z N.Dynamics and control of cranes: a review[J]. Journal of Vibration and Control, 2003，9(7)：863-908.

[9] 张祖鹰.堆垛机模糊反馈校正控制系统的设计[J].制造业自动化，2010，32(12)：48-50,53.

[10] 李新明，王好臣，林春梅，等.堆垛机速度智能控制的优化研究[J].机械工程与自动化，2012(3)：112-114.