基于多项式插值的分数延时滤波器的FPGA实现

肖美龄，龚晓峰

（四川大学电气信息学院，四川成都 610065）

数字化可调节的分数延时滤波器（fractional delay filter，FDF）在信号重构，回声消除，定时同步，任意分数倍采样率转换等许多领域都有着广泛的应用[1-3]，因此被人们广泛研究。但由于理想的FDF脉冲响应无限长，导致在实际系统中实现非常困难。基于farrow结构[4]的多项式插值滤波器很好地解决了这个问题[5]。

近年来，关于FDF的研究也有很多，文献[6]对farrow结构进行了改进，提出了广义改进型farrow结构，文献[7]采用加权最小二乘法与积分计算目标误差函数、矩阵的行拉直、矩阵的三角分解相结合的方法设计FDF，文献[8]提出了插值多项式的阶数和分段数的选择策略。文献[9]采用基于样条插值的方法来设计分段插值多项式。文献[10]采用基于最小二乘的方法来设计分段插值多项式。以上方法都是在理想情况下的研究，虽然有效提高了FDF的设计精度，但工程实现上依然比较复杂，文献[11]结合流水线技术与分布式算法减少了乘法器的使用，但运行时钟较低，且分数延时不可调节，基于分段二次抛物线插值算法设计的FDF相对于三次插值性能同样优越且实现更加简单[12]，但基于二次分段抛物线插值滤波器在进行延时估计时存在局部极值问题。本文通过仿真分析选择合适设计参数解决了发现的极值问题，并使用可编程逻辑器件FPGA来实现了该FDF，可用于实际的无线电设备中。

1 多项式插值在信号处理中的应用

1.1 拉格朗日多项式插值

对许多的实际问题，往往需要用函数y=f（x）来表示来出某种内在的规律，我们只能通过观测到的部分数值来构造一个能反映函数特性并且便于计算的简单函数p（x）来近似f（x），这就是插值法[13]。

常见的插值算法有拉格朗日插值、牛顿插值等，由于在计算量、计算复杂度和精度方面的优势，比较常用的是拉格朗日插值算法[14]。拉格朗日插值多项式：

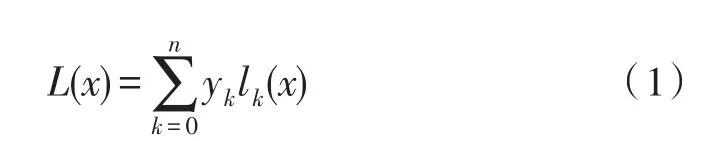
式（1）中，每个lk（x）为拉格朗日插值基函数，其表达式为

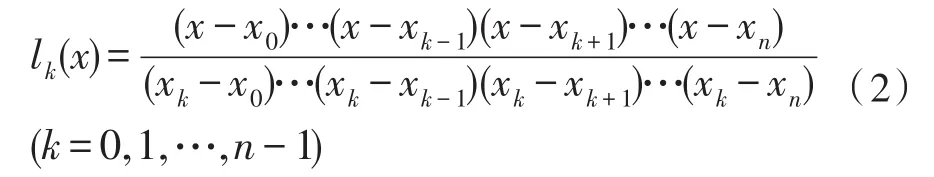
1.2 分数延时滤波器

延时在通信系统中是不可避免的，数字延时分为整数延时和分数延时，整数延时容易实现和控制，然而，当期望的延时是分数倍的，就需要通过FDF来实现。

当一个信号延迟了tD，延迟后信号表示为y（t）=x（t-tD）。转换成离散信号t=kT，T表示采样间隔，可以表示出

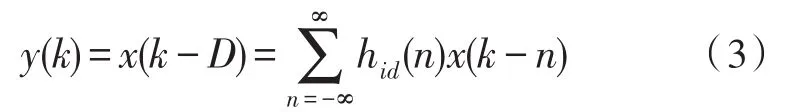
式（3）中，D是一个正实数，并且可以分成一个整数部分和一个小数部分

式（4）中，m是离散信号的整数延时，μ是离散信号的小数延时。当D不是一个整数时，在两个插值样点x（k-m）和x（k-m-1）之间，可以用一个带限插值来逼近y（k）。理想的FDF系数可以表示为

理想的无限长FDF是不可实现的，因此用一种近似的解决方案

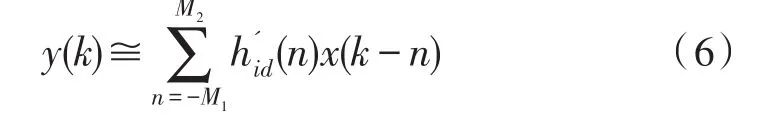
式（6）中，

拉格朗日多项式插值滤波器被广泛用于小数延时估计中。用拉格朗日多项式插值来逼近，N阶的拉格朗日插值器系数为

针对4个插值基点，可以设计为二次分段抛物线插值器，多项式系数为

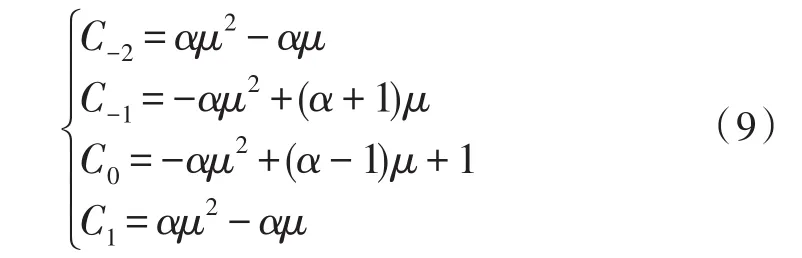
其中α为设计参数。

在医学信号处理，数字通信，时间延迟估计等过程中会需要实现分数倍采样率的转换，采样率转换可归纳为一个重采样的过程：先将采样信号x（mTs）重建为模拟信号x（t），再对模拟信号重采样得到所需频率的采样信号

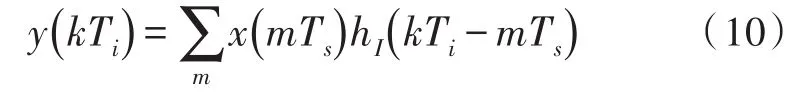
式（10）中Ts和Ti分别为输入和输出采样间隔。但Ts/Ti的值一般不是有理数。将这里的模拟滤波器hI（t）用（8）式表示的拉格朗日插值滤波器表示。并定义基本指针mk，分数间隔μk，滤波器指针如下。

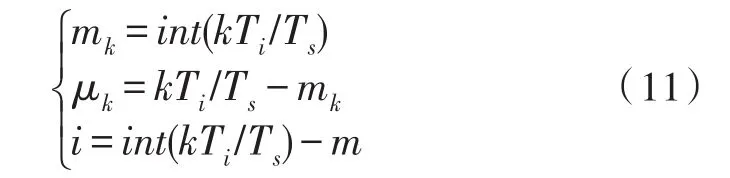
则（11）式可改写为

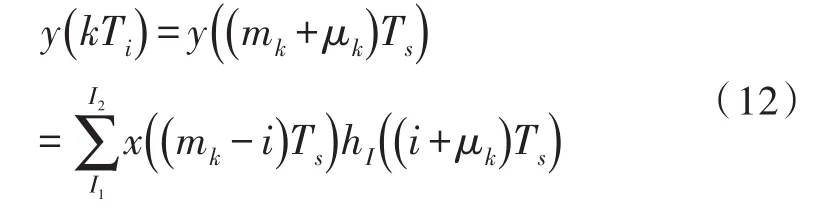
实时计算μk和mk就可以实现分数倍采样率的转换。通过调整数字延时μk，可以改变频率转换的比例。

2 延时估计精度分析

2.1 小数延时估计中的局部极值问题

在时延估计算法中，相关法是最经典的时延估计方法，它通过信号的自相关函数滞后的峰值估计信号之间延迟的时间差。这种方法简单易懂，容易实现[15]。通过相关法来验证小数延时估计精度，两接收信号的互相关函数为

式（13）中：x1（t）为源信号，x2（t+τ）为小数倍延迟后信号，由自相关函数的性质可知

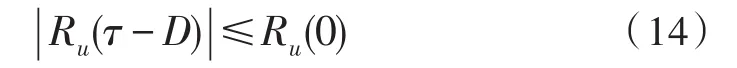
即当τ-D=0时，两个接收信号的相关性最大，选择τ=D作为延时估计值。则即当相关性函数取得最大值时的τ为估计出的延迟。

为了对几种插值方法的延时估计精度进行仿真分析。需要产生原始基带信号和其准确延迟，这里我们巧妙运用抽取原理。为更好地切合实际信号，在MATLAB中随机生成有效带宽1 kHz，采样率1 MHz的离散信号d0。进行100倍的抽取操作，得到信号d1，由抽取理论可知抽取后信号d1实际采样率为10 kHz，且频谱不会发生混叠。并通过抽取得到d1信号经过原5个采样间隔后的100倍抽取信号d2。d1即为d2经过0.05个延时后信号。软件仿真流程如图1。

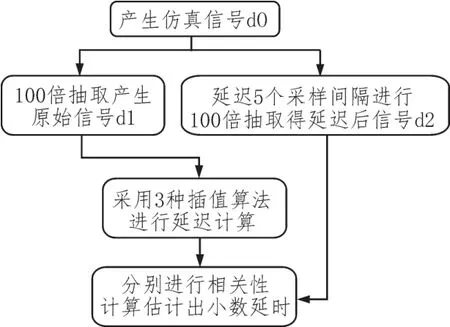
图1 小数延时估计流程图

将d2以0.001个采样间隔为步进从-1至1进行延迟计算，求出的每组延迟结果与d1求相关性函数值得到一条相关性曲线。3种不同的插值分别得到3条相关性曲线。如图2所示。

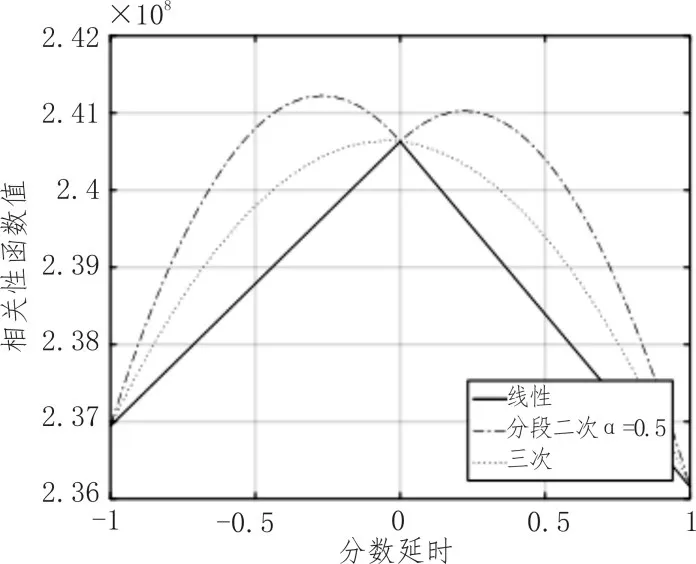
图2 延时估计精度对比（α=0.5）

分析图2，线性插值极值点在0点处，而α取值为0.5时的分段二次抛物线插值存在两个极值点，均无法有效估计出分数倍延迟，三次插值极值点在-0.046出现，即估计出当前延时为0.046个采样间隔，相比于实际0.05个采样间隔的延时，延时估计效果很好。

2.2 最终实现方案的确定

在使用硬件实现插值滤波器时，二次分段抛物线插值滤波器（α=0.5）相比于三次拉格朗日插值实现过程上更为简单，主要取决于其特殊的滤波器系数使得数据运算规模和乘法器都减少，但是由于二次分段抛物线插值（α=0.5）存在的局部极值问题。如何选取其中的设计参数α来达到逼近于三次插值的性能而又不增加计算复杂度是目前需要解决的问题。

用二次插值去逼近三次插值有很多方法，决定于逼近准则。用拉格朗日三次插值多项式表示出4个插值样点中最中间的值为

拉格朗日二次插值基函数用点（xk，yk），（xk+0.5，yk+0.5），（xk+1，yk+1）可以表示为

将式（15）、（16）带入式（17）可以得到

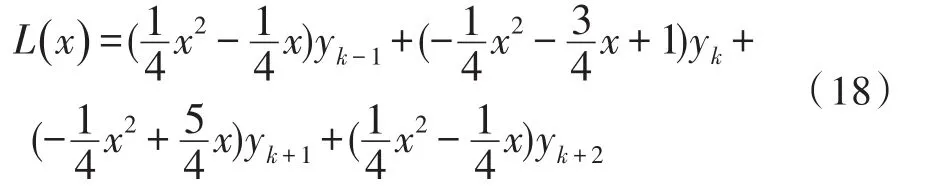
最后我们得到了新的二次分段抛物线插值器系数

以与图2相同的方法验证分段二次抛物线插值当α=0.25时的延时估计精度。

图3 延时估计精度对比（α=0.25）

分析图3可以得出二次分段抛物线插值（α=0.25）不存在局部极值问题，极值点出现在-0.045处，即估计出延时为0.045个采样间隔，与三次插值估计出的0.046非常接近。

2.3 FPGA实现

本文的FDF硬件组成划分为2个子模块：变速率参数计算模块和小数延时模块。图4就是本文的FPGA硬件设计整体框图。对于图4中的小数倍延迟子模块，本文在基于分段二次插值farrow结构的基础上加入了并行设计的思想进行了改进，减小了输出延时，如图5所示。并进行了计算复杂度的对比如表1所示。

对于变速率参数计算模块，每个插值点的插值基点与小数间隔都不相同，需要实时计算。为了保证输出精度，小数间隔的中间计算过程采用定点整形运算。

将式（11）中mk和μk改进为递推公式如下，简化计算[16]。

式（20）、（21）中，fs和fi分别为输入和输出采样率，在（20）式两边同时乘以fi可得

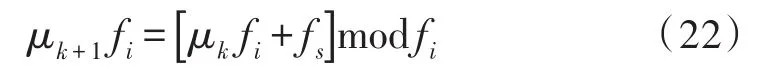
计算μk的值可以变为计算μkfi的值，中间计算全都采用整形运算，只需在最后进行浮点除法运算求得μk。为了保证运算精度，μk用32位浮点数表示，输入数据量化为32位整形数，在进行乘法运算前通过整形转浮点IP核转化为32位浮点数。

图4 FPGA硬件设计整体框图

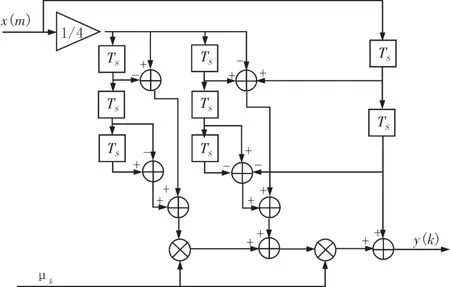
图5 改进的FDF实现结构（α=0.25）

表1 不同插值器的计算复杂度

最后，本文对基于farrow结构的分段二次插值滤波器（α=0.25）进行了Verilog HDL编程实现了FDF（抽取和内插），并在Altera的FPGA板（EP4CGX150CF23I7）上下载成功，quartusⅡ上单路信号仿真波形如下

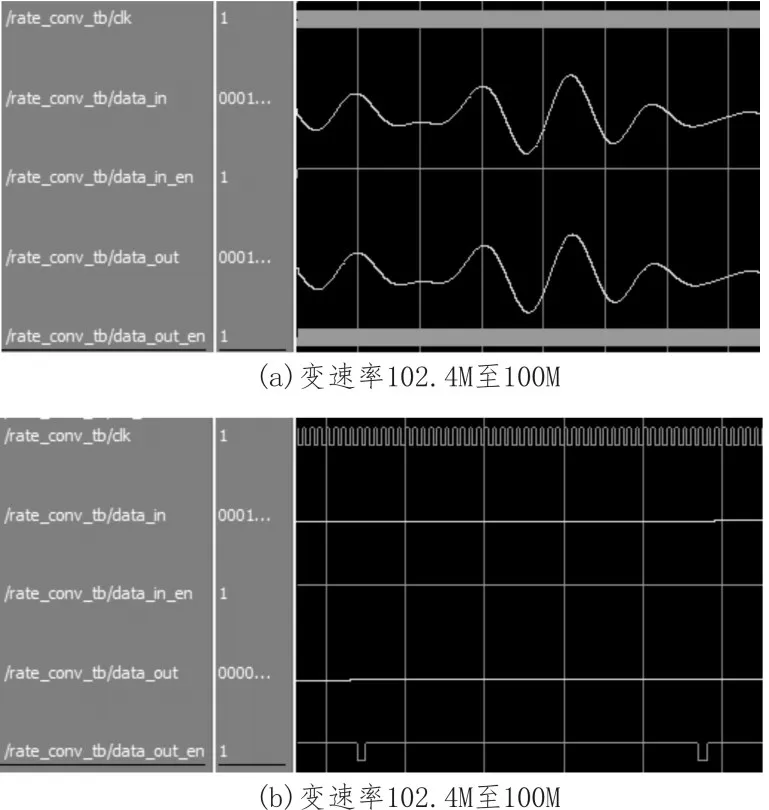
图6 FDF模块仿真和仿真局部放大图

图7 仿真数据对比

本文采用与MATLAB平台技术并行的方式，在MATLAB平台上也对FDF进行了软件建模，将硬件模块输出结果与软件模型输出结果及原始信号对比。如图6所示，时钟信号为102.4 MHz，输入数据数率为满时钟速率，输出数据数率为100 MHz，输出数据有效由data_out_en信号指示。图7为根据数据有效指示导出的数据，由于是进行抽取仿真，在同一采样点下，输出信号相比原始信号呈现延迟状态，可以看出模块输出与软件模型输出几乎完全一致，误差是由定点运算的量化误差造成。

3 结 论

本文对基于farrow结构的分段二次插值的延时估计效果进行研究，发现分段二次插值在进行延时估计时存在局部的极值问题，针对该问题进行了分析对比从而提出了一种解决方案，并基于该方案实现了该FDF，实验证明采用本文结构来实现FDF具有消耗硬件资源少，运算精度高，可进行信号的实时处理等优点。

[1]Vesma J，Saramäki T.Design and properties of polynomial based fractional delay filters[C]//IEEE International Symposium on Circuits and Systems，2000（1）:104-107.

[2]Abbas M，Gustafsson O，Johansson H.On the fixed-point implementation of fractional-delay filters based on the farrow structure[J].Circuits&Systems I Regular Papers IEEE Transactions on，2013，60（4）:926-937.

[3]Eghbali A，Johansson H，Saramäki T.A method for the design of Farrow-structure based variable fractional-delay FIR filters[J].Signal Processing，2013，93（5）:1341–1348.

[4]Farrow C W.A continuously variable digital delay element[J].IEEE InternationalSymposium on Circuits and Systems，1988，3:2641-2645.

[5]Erup L，Gardner F M，Harris R A.Interpolation in digital modems- part II:implementation and performance[C]//IEEE Transactions on Communications，1993，41（6）:998-1008.

[6]Hunter M T，MikhaelW B.A novel farrow structure with reduced complexity[J]. IEEE International Midwest Symposium on Circuits and Systems，2009（10）:581-585.

[7]周晶，王敬时.分数延时FIR滤波器设计及仿真[J].信息化研究，2013（4）:24-27.

[8]Babic D，Vukotic S.Estimation of the number of polynomial segments and the polynomial order of prolonged Farrow structure[C]//Telecommunications Forum Telfor.Belgrade，2014:461-464.

[9]Blu T，Thevenaz P，Unser M.Complete parameterization of piecewise polynomial interpolation kernels[J].IEEE Transactions on Image Processing，2003，12（11）:1297-1309.

[10]Pulikkoonattu R，Subramanian H K，Laxman S.Least square based piecewise parabolic interpolation for timing synchronization[C]//Radio and Wireless Symposium.IEEE Xplore，2008:155-158.

[11]陈光辉，曾以成.分数延迟FIR滤波器设计及FPGA 实现[J].微计算机信息，2010，26（20）:172-174.

[12]Eltawil A M，Daneshrad B.Piecewise parabolic interpolation for direct digital frequency synthesis[C]//IEEE Custom Integrated Circuits Conference，2002，21（5）:401-404.

[13]李庆扬，王能超，易大义.数值分析[M].武汉:华中科技大学出版社，2006.

[14]陶伟，刘发林，王昊禹，等.一种非迭代的基于插值滤波器的小数延时估计算法[C]//全国微波毫米波会议论，合肥，中国电子学会，2015:683-686.

[15]行鸿彦，唐娟.时延估计方法的分析[J].声学技术，2008，27（1）:110-114.

[16]Gardner F M.Interpolation in digital modemspart I:fundamentals[C]//IEEE Transactions on Communications，1993，41（3）:501-507.

[17]宋鹏，田乐.基于FPGA的时间同步精度的设计与实现[J].西安工程大学学报，2014，28（1）:89-93.

[18]彭喆，付盛坤.基于FPGA的内嵌滤波算法的高速PCI采集卡设计[J].工业仪表与自动化装置，2017（3）:74-77.