面向云计算的混合同态加密算法研究

战 非 ，赵 侃 ，曹国震 ，张少茹

（1.西安航空学院计算机学院，陕西西安710077；2.西安交通大学医学院护理系，陕西西安710049）

随着云计算技术的普及，海量的用户数据需存储在云服务器端，数据的隐私保护一直是困扰云计算广泛应用的重要问题。传统的加密技术先对明文加密，然后将密文存储在云服务器端，但是当用户需要在云服务器端进行检索、计算和统计操作时，传统的加密方案是无法实现对密文操作等价于明文操作[1]。

近年来全同态加密算法的提出和发展确为之提供了可能。所谓全同态加密指对明文进行加减乘除的多项式运算再加密，与对加密后的密文进行同样的运算的结果是等价的[2-3]。目前较为成熟的同态方案包括基于理想格设计的同态加密体制、基于整数的全同态加密机制以及非Squash和Bootstrapping的加密体制等。但目前提出的这些算法在计算效率和计算深度上都没有达到理想状态，所以同态加密还有很大的研究和发展的空间。

文中通过对同态加密原理的分析，结合较为成熟的RSA和Bresson这两种部分同态的加密算法，在限定理想算法参数的基础上，通过对其二者进行拆分和混合，提出一种BRH（Bresson-RSA Homomorphic Encryption Algorithm）全同态加密算法，该算法通过实验，实现了在云服务器端针对密文进行“不解密”的多项式计算，等价于对明文数据的全同态操作。

1 全同态加密理论分析

所谓加密算法的同态性是指，当两段明文x和y，当其二者满足Dec(En(x)⊗En(y))=x⊕y，En()代表加密运算，Dec()代表解密运算，⊕代表明文域的运算，⊗代表密文域的运算。若⊕代表加法运算，称该加密满足加法同态，如本文后面分析的Bresson算法；若⊗代表乘法时，称该加密满足乘法同态[4-5]，如本文分析的RSA算法。如加密算法能够实现任意多次加法和乘法运算，但仍然同时满足加法同态性和乘法同态性，则称其为全同态算法，可如下式表示：

f代表满足满足加减乘除运算的任意计算函数。

全同态加密的性质在云计算中具有广阔的应用前景，用户可以在云端委托不信任的第三方对数据进行统计和计算而不会泄露明文数据，相对于传统的加密方案，极大地提高了云计算效率[6]。

2 RSA算法及同态分析

RSA算法通过大数难以分解的数学问题保证其安全性，密钥长度达到1024位[7]。RSA是一种能够抵御目前绝大多数密码攻击的公钥加密算法，其密钥产生及加密解密流程如下：

1）产生两个大素数p和q，p≠q；

2）计算n=p×q，根据欧拉公式φ(n)=(p-1)×(q-1)；

3）随机选择满足 gcd(e,φ(n))=1的(e,n)作为公钥；

4）计算d=e-1modφ(n)，以(d,n)作为私钥；

5）对明文按式C=pemodn进行加密；

6）对密文按式P=Cdmodn进行解密；

现对RSA算法的同态性进行分析：

设算法公钥为(e,n)，私钥为(d,n)，明文为m，密文为c。加密解密过程如上所述，对于明文m1和m2进行加密可得：

由以上分析可得RSA算法具有乘法同态性，由于其不满足加法同态，所以RSA算法是一种满足乘法同态的部分同态加密算法。

3 Bresson算法及同态分析

Bresson加密算法在2002由Cramer和Shoup提出的一种在公钥密码体制的通用范式的基础上发展而来加密算法，安全性通过规约到因式分解的数学难题来进行保证[8]。Bresson算法的密钥生成及加解密过程如下：

1）设N=pq，其中p和q为素数。若p0和q0也为素数，且满足p=2p0-1,q=2q0+1，G为模N2的二次剩余循环群。

4）解密过程当已知密钥α，按下式进行解密

现对Bresson算法的同态性进行析：

设明文为m1和m2，通过算法加密的密文分别为En(m1)=(A1,B1)和En(m2)=(A2,B2)，其中

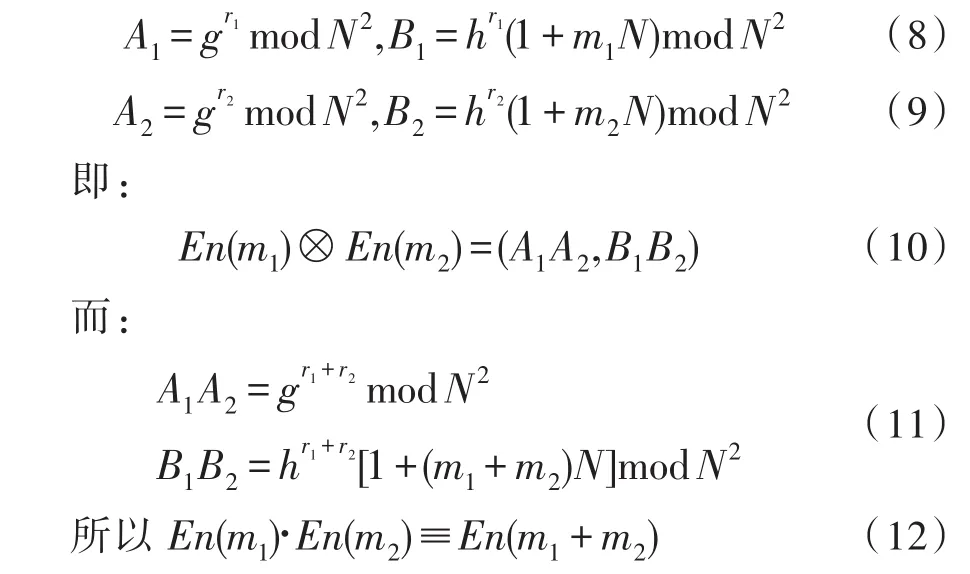
因此，Bresson算法和RSA算法不同，它具有加法同态性。

4 BRH混合全同态算法设计

全同态算法最大的优势就是使密文的计算和统计等同于对明文的操作，特别是在云计算中，需要通过云服务器对密文数据进行检索和计算，经过全同态加密方案的数据省去了二次解密加密的过程，实现数据在云端“不解密”的使用，能够大大的提高云服务的响应时间[9]。

但是前文提到的基于理想格的全同态加密方案在实现上还存在巨大的困难，密钥的生成时间过长、密钥尺寸过大、加密过程中噪声的产生，计算维度过低等缺陷使该类算法应用上较为困难[10]。文中以实现云服务器端对密文实现全同态操作为出发点，提出了一种混合RSA和Bresson算法的全同态BRH（Bresson-RSA Homomorphic Encryption Algorithm）加密算法。

BRH算法实现原理为：首先生成RSA和Bresson算法的密钥；然后对计算多项式进行代数拆解，分解为纯加减计算向量和纯乘除计算向量；根据Bresson算法的加法同态性对加减多项式进行加密，根据RSA算法的乘法同态性对乘除多项式进行加密；在云服务器端对密文进行多项式计算并根据提出算法进行还原，最终实现全同态操作。

首先为了实验仿真的便利以及算法复杂度的考虑，设定该算法在理想条件下执行。具体指同态的加减乘除操作均为整数，且运算多项式不包含常数。

当计算过程中若出现浮点数进行浮点数到整数的映射，映射过程如下：

1）设浮点数小数位数为τ且非负整数，浮点数表示为γ=γ0∙γ1γ2…γτ。

2）则浮点数可表示为：

γ=γ0×100+γ1×101+…γi×10τ。

3）定义映射函数为：

f(γ)=γ0×100+γ1×101+…+γi×10τ在映射函数f下降浮点数表示为(f(γ),τ)。

4）定义逆映射f-1为：

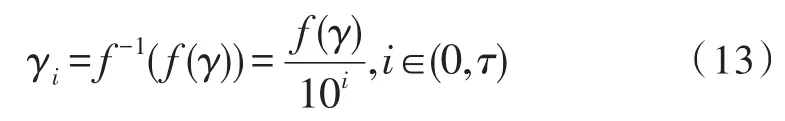
则 (f(γ),τ)之间的加法操作为：

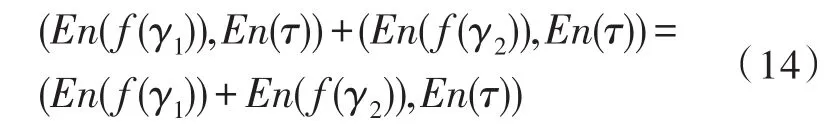
乘法操作表示为：

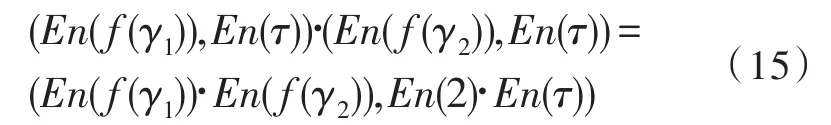
减法操作同式（14）类似，除法操作同式（15）类似。由此实现操作数从浮点域向整数域的映射。

设f+,-表示加减操作，f×,÷代表乘除操作，设不带常数的计算表达式为：

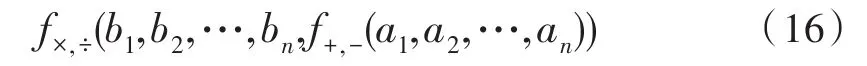
BRH算法具体实现流程如下所示：

1）根据上述分析的RSA算法和Bresson算法规则，生成RSA算法的公钥PKR和私钥SKR；生成Bresson算法的公钥PKB和私钥SKB。

2）将需操作计算的式（16）拆分为单纯加减计算向量α=(a1,a2,…,an)+,-和单纯乘除向量。

3）对计算向量α进行Bresson加密得EnPKB(α)=(EnPKB(a1),…,EnPKB(an))+,-，将密文发送至云服务器，在服务器端进行不解密相同运算f+,-(EnPKB(a1),…,EnPKB(an))，然后返回加密密文。然后通过Bresson私钥进行解密得到向量α的值。

4）对计算向量β进行RSA加密得，将密文发送至云服务器，在服务器端进行不解密相同运算，然后返回加密密文。然后通过RSA私钥进行解密得到向量β的值。

5）对|α|与|β|进行还原，完成服务器端的对应同态操作。

5 云仿真实验

本次实验在Java环境中配置SSH框架，实现Hadoop平台搭建集群模拟云环境，集群由6台计算机组成，其中一台配置为“CPU I7-4790，8G内存，主频 3.2 GHz，1T硬盘”作为 NameNode，扮演 Master和JobTracker的角色。为了更好模拟云环境，其余5台计算机选取实验室中配置各不相同的5台机器，作为Slave和DataNode，即云计算中的计算节点。MapReduce过程对明文以默认值为单位划分数据块，不变化数据块大小。重写map（）函数实现混合加密算法。

第一部分实验：为更直观表现算法同态操作的特点，规定正整数进行(x+y)+(a+b)×z的简单表达式计算。通过变化随机产生的正整数取值范围，对比直接对数据明文进行计算和采用BRH算法计算在云平台下的执行时间如图1所示。

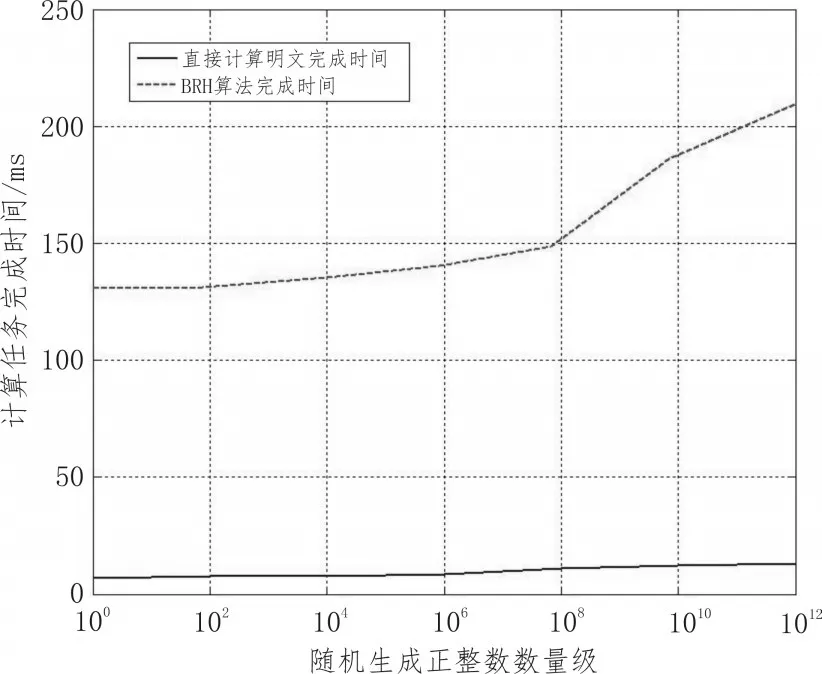
图1 不同量级数据计算对比图

由图1分析可得，对于明文直接计算，以目前搭建云平台的硬件水平没有任何压力，在取值量级增加的情况下计算时间没有明显的变化。但是通过混合同态BRG算法进行计算，虽然是在理想实验条件下通过代数结构实现，但是耗时明显增大，在一定范围内的密文规模下执行效率较为稳定，但是随着数据量级继续增大，计算时间有大幅递增的趋势。这表现出了目前同态计算的特点，并且由于混合算法中的RSA算法在密钥生成时计算量较大，也降低了算法效率。

第二部分实验：随机生成102内的正整数，同时以四分之一概率随机生成不同数量的加减乘除运算符，进行对正整数进行叠加运算，遇到浮点数按本文上述的映射规则进行整数映射。统计模拟计算规模（以运算符数量代表）与执行效率之间的关系。实验结果如图2所示。

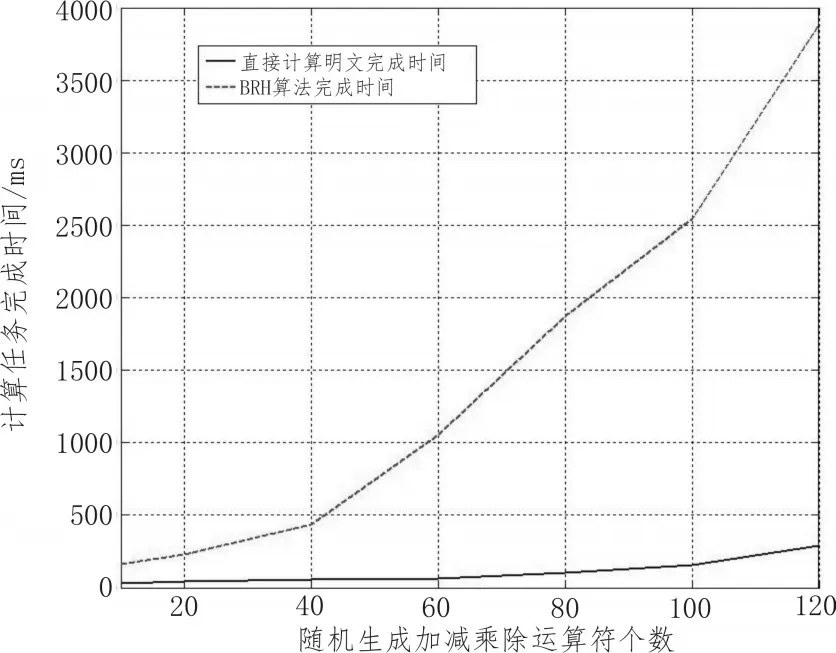
图2 不同运算符个数计算对比图

由图2分析可得，在当前搭建的云环境中，对明文数据直接进行计算同样没有压力，执行效率平稳。但是混合同态运算受运算规模制约较大，执行时间表现出线性递增。原因是由于操作符的数量直接决定了BRH算法进行混合加密解密的次数，成为制约该方案执行效率的瓶颈。

6 结束语

本文对同态加密理论进行了简要分析，指出了目前全同态加密在实现上的不足，在研究RSA算法和Bresson算法的结构和各自具有的同态性的基础上，提出了一种便于理解和实现的混合全同态加密BRH算法。该算法适合于应用在云计算中，能够实现在云服务器端进行不解密的多项式计算，最后通过搭建云实验环境，对提出算法进行了仿真实验，验证了该算法的正确性。然而，该算法的局限性也非常大，首先算法的执行是基于理想实验参数，都是进行正整数的运算，并且计算量级较小，对于浮点数进行了不精确的映射，影响了算法的精度。其次，云平台的集群规模也较小，没能较为完全的模拟实际云计算环境的复杂情况，这些都需要在日后的研究中进行进一步改进和研究。

[1]王鹤鸣.从信息化发展历程看密码学发展——专访西安电子科技大学通信工程学院王育民教授[J].信息安全与通信保密，2011，9（12）:13-19.

[2]徐鹏，刘超，斯雪明.基于整数多项式环的全同态加密算法[J].计算机工程，2012，38（24）:1-4.

[3]王勇.随机函数及其在密码学中的应用研究[J].信息网络安全，2012（3）:17-18.

[4]周燕，刘培玉，赵静.基于自适应惯性权重的混沌粒子群算法[J].山东大学学报理学版，2012，47（3）:1-7.

[5]林如磊，王箭，杜贺.整数上的全同态加密方案的改进[J].计算机应用研究，2013，30（5）:1515-1519.

[6]汤殿华，祝世雄，曹云飞.一个较快速的整数上的全同态加密方案[J].计算机工程与应用，2012，48（28）:117-122.

[7]侯佩，寇雅楠，黄利斌.混合加密体制在数字签名中的应用[J].计算机工程与计，2011，32（6）:1942-1945.

[8]周福才，徐箭.格理论与密码学[M].北京:科学出版社，2013.

[9]孙国梓，董宇，李云.基于CP-ABE算法的云存储数据访问控制[J].通信学报，2011，32（7）:146-152.

[10]刘波.云计算的安全评估之其应对措施探讨[J].移动通信，2011，35（9）:34-37.

[11]光焱，顾纯祥，祝跃飞.一种基于LWE问题的无证书全同态加密体制[J].电子与信息学报，2013，35（4）:988-993.

[12]白健，刘慧，张若箐.一种新型基于R—LWE的公钥密码体制[J].北京电子科技学院学报，2013，21（2）:46-49.

[13]王永涛.基于属性密码体制的相关研究[D].上海：上海交通大学，2011.

[14]Vrakerski Z， Centry C， Vaikuntanathan V.（Leveled）fully homomorphic encryption without bootstrapping[C]//Proc of Innovations in Theoretical Computer Science 2012（ITCS 2012）.New York:ACM，2012:309-325.

[15]Centry C，Haleci S.Fully homomorphic encryption without squashing using depth-3 arithmetic circuits[C]//Proc of the 52th IEEE Annual Symp on Foundations of Computer Science（FOVS 2011）.Piscataway，NJ:IEEE，2011:107-109.

[16]M.Sipser.Introduction to the Theory of Computation[M].Thrid Edition.Wadsworth Publishing Co Inc，2012.