一种考虑死区的PMSM无速度传感器滑模辨识及控制

黄亚军，史旺旺



一种考虑死区的PMSM无速度传感器滑模辨识及控制

黄亚军，史旺旺

（扬州大学水利与能源动力工程学院，江苏 扬州 225009）

本文设计了一种基于旋转坐标系自适应滑模观测器并考虑死区补偿的转速和转子位置估算方法。为了解决传统估算方法导致的抖振问题，引进了近似滑模Sigmoid函数，提高了系统的可靠性。采用 Lyapunov 函数对角速度进行辨识，保证了系统稳定，取消了数字锁相环，使得算法变得更加简单。针对逆变器死区对估计模型的影响，引入了一种坐标变换补偿法的死区补偿算法到自适应滑模观测器控制中，消除了实际电机和模型电机之间的相位误差。仿真和实验结果表明，所提出的算法具有较强的鲁棒性，加快了系统的响应速度。

旋转坐标系；死区补偿；Lyapunov 函数；滑模观测器；永磁同步电机；转子

0 前言

永磁同步电机由于其磁通密度比较高、体积相对较小、重量轻、效率高等优点被广泛地应用于化工、医疗器具、机器人、机床、航天等方面。然而各种复杂的环境使得编码器的可靠性大大降低，并且不使用编码器这样的机械传感器会使得成本降低。因此，无速度传感器控制的研究成为了交流伺服研究领域的一个重要方向。

无速度传感器控制的核心是对转速和转子位置的估计，近年来，很多专家学者提出了各种不同的估计方法。文献[1]~[2]使用了神经网络法和卡尔曼滤波法对转子的转速和位置进行了估计，但他们的方法都相对比较复杂，使得控制的算法结构以及参数的设计都比较困难。文献[3]通过对比仿真方法指出，滑模变结构控制具有比神经网络法和模型参考辨识法更好的鲁棒性。文献[4]建立了假定同步旋转坐标系模型，通过控制假定同步坐标系与实际坐标系的之间的角度差来进行估计转速，这种方法使系统不具有全局收敛性。文献[5]~[7]在传统的滑模观测器基础上引进了Sigmoid函数，这种方法克服了传统观测器存在的抖振问题，简化了传统滑模观测器，但文中速度和转子位置估计的精度和反电势的幅值有关，在低速甚至在速度为零时会导致反电势过小而无法估计转速和转子位置。文献[8]通过高频注入的方法给电机注入高频电压，再通过电机的电流来推算出转速和转子位置，可以解决电机在低速时无法估计的问题，但注入的高频信号会带来新的噪声问题，并且由于电机对硬件的要求导致其局限于内埋式电机。文献[9]~[12]引入锁相环控制对PMSM的转速进行估计，建立了一个新型的无速度传感器PMSM矢量控制调速系统，然而引入锁相环需要进行大量计算，降低了系统的响应速度。

本文针对逆变器驱动的永磁同步电机无速度传感器控制提出了一种新的方法。该方法以常规假定旋转坐标法为基础，结合模型电机法，通过滑模观测器对模型电机电流进行控制，使模型电机电流与实际电机电流之间的误差为零。再通过Lyapunov理论建立转速自适应率并论证了其收敛性[13-14]。同时，在模型电机中考虑逆变器死区引起的电压变化，本文引入了一种坐标变换补偿法的死区补偿算法到自适应滑模观测器控制中[15]。通过仿真和实验结果表明了系统具有稳定性、快速性以及无超调的特性。

1 永磁同步电机数学模型

永磁同步电机在dq坐标系下的定子电压方程为：

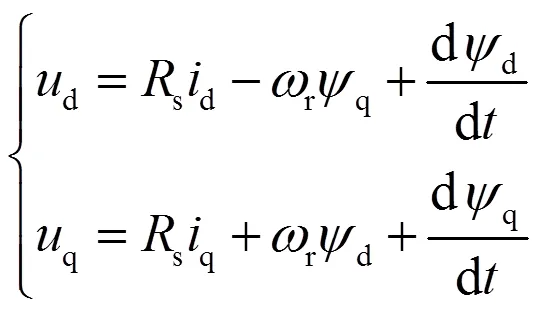
定子磁链方程为：

电磁转矩方程可表示为：

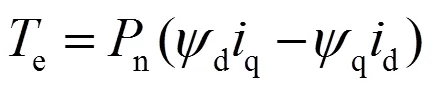
电机转子机械运动方程可表示为：

2 自适应滑模观测器设计

2.1 PMSM的转速和位置估计方案

由式（6）和式（7）得到动态电流估计偏差方程

对式（9）化简和转换后可得：

对式（10）求导可得：

若令

式中，为符号函数幅值。

对其积分可得：

则估计转子位置角即为：

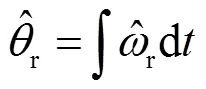
2.2 基于Lyapunov法的控制器设计

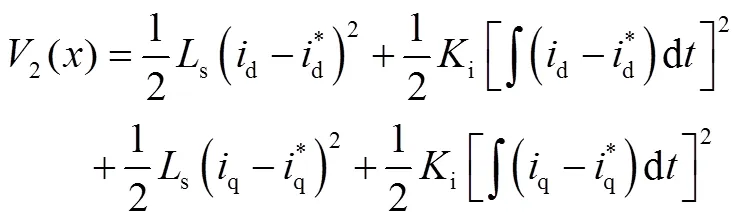
对Lyapunov函数求导可得：

当电机完全同步时，得：

式中，p为控制比例系数。转化式（19）可得到实际控制律为：

式中，dc为逆变器直流母线电压。

3 仿真和实验结果及其分析

图1 未加入死区补偿的转子位子角仿真波形

针对以上波形的分析说明，在理想的仿真条件下，基于旋转坐标系自适应滑模观测器能够使得系统具有良好的动态响应特性和稳态特性。

为了验证本文提出算法的实际可行性，进行了实验测试。实验中搭建了基于TMS320F28335数字信号处理器的电机实验平台，采用IGBT全控型开关管构建的电路进行能量转换，电机部分采用型号为FXBS180的永磁同步无齿轮曳引机，实验时的参数和仿真的一致。本文采用了一种方法将转速和转子位置角归一化，同时要保证它们的周期与原来的相同，然后将其调制成PWM波，再通过一个一阶RC滤波电路就可以还原转速和转子位置角信号，通过示波器显示出来。

图3和图4分别为旋转坐标系自适应滑模观测器加入死区补偿后的估计转速与实际转速、估计转子位置角和实际转子位置角对比的实验波形图。图3中估计转速响应速度快，稳定后与实际PMSM的转速重合。图4中模型电机的转子位置角和实际转子位置角在正方向转的时候有一点误差，但在误差范围之内，在反方向时波形重合。

图2 加入死区补偿后仿真波形

图3 加入死区补偿后的转速实验波形

图4 加入死区补偿后的转子位置角实验波形

从实验波形可以看出，实验结果和仿真结果一致。因此，本文提出的基于旋转坐标系自适应滑模观测器的算法能够得到满意的效果。

4 结论

本文提出了一种新型的基于旋转坐标系自适应滑模观测器的永磁同步电机无速度传感器控制的算法。算法充分考虑到死区效应对逆变器输出电压电流的影响，并引入了一种坐标变换补偿法的死区补偿算法。利用Lyapunov稳定性定律推导出估计转速的自适应率、模型电机的转子位置角。选取适当的滑模增益来克服系统不确定性和参数变化的影响。对模型电机和实际PMSM之间电流误差的控制采用Lyapunov法进行，保证系统全局的稳定性。最后，对所提出的仿真和实验进行了验证，结果表明，所提出的算法对PMSM转速和转子位置的估计非常精确，是一种实用的估计转速和转子位置的方法。

[1] 李鸿儒, 顾树生. 基于神经网络的PMSM速度和位置自适应观测器的设计[J]. 中国电机工程学报, 2002(12): 32-35.

[2] 邱忠才,郭冀岭,王斌等. 基于卡尔曼滤波滑模变结构转子位置观测器的PMSM无差拍控制[J]. 电机与控制学报, 2014(04):60-65.

[3] Brahmi J, Krichen L, Ouali A. A comparative study between three sensorless control strategies for PMSG in wind energy conversion system[J]. Applied Energy, 2009, 86(9): 1565-1573.

[4] Yukinori I, Koji Y, Shigeo M, et al．Effectiveness of voltage error compensation and parameter identification for model-based sensorless control of IPMSM[J]．IEEE Transactions on Industrial Applications, 2009, 45(1): 213-221．

[5] 朱喜华, 李颖晖, 张敬. 基于一种新型滑模观测器的永磁同步电机无传感器控制[J]. 电力系统保护与控制, 2010, 13:6-10.

[6] Hongryel Kim, JubumSon, Jangmyung Lee. A High-Speed Sliding-Mode Observer for the Sensorless Speed Control of a PMSM [J]. IEEE Transactions on industrial electronics ,2011, 58(9):4069-4077.

[7] 张晓宇. 变结构控制系统抖振问题的研究[D]. 浙江大学, 2003.

[8] 鲁文其, 胡育文, 杜栩杨, 等. 永磁同步电机新型滑模观测器无传感器矢量控制调速系统[J]. 中国电机工程学报, 2010, 33:78-83.

[9] 彭澍,章跃进. 嵌入式永磁同步电动机高频注入法无位置传感器控制研究[J]. 微特电机,2014(4):53-56.

[10] Degner M W，Lorenz R D．Using multiple saliencies for the estimation of flux，position and velocity in AC machines[C]．IEEE．IAS Conf. Rec.，New Orleans．1997：760-767．

[11] Li H R，Wang J H，Gu S S，et al． A Neural-network-based Adaptive Estimator of Rotor Position and Speed for Permanent Magnet Synchronous Motor[C]. IEEE ICEMS 2001: 735-738．

[12] 缪学进,李永东,肖曦. 高频信号注入无速度传感器永磁同步电机控制系统[J]. 电气传动, 2007(03):11-14.

[13] 刁利军，刘志刚，孙大南等. 基于Lyapunov理论的交流传动系统建模和稳定性分析[J]. 北京交通大学学报，2010(05)：32-36.

[14] Komurcugil H，Kukrer O. Lyapunov-based control for three phase PWM AC/DC voltage-source converters[J]. IEEE Transactions on Power Electron，1998(13):801-813.

[15] 郑伟,季筱隆,刘玮等. 一种基于电流矢量的死区时间补偿方案[J]. 电气传动, 2005(04):34-36.

Sensorless Sliding Mode Identification and Controlof Permanent Magnet Synchronous Motor Considering Dead-Time

HUANG Yajun, SHI Wangwang

(Hydraulic and Energy Engineering College, Yangzhou University, Yangzhou 225009, China)

A new speed and rotor position estimation methodby adaptive SMO based on rotating coordinate system considering dead-time is designed. To solve the chattering problem caused by the traditional estimation method, the approximate sliding mode Sigmoid function is introduced to improve the reliability of the system. The Lyapunov function is used to identify the angular velocity, which ensures the stability of the system, and cancellation of the digital phase locked loopmakes the algorithm simple. Considering the influence of dead time on the estimation model, a dead time compensation algorithm based on coordinate transformation is introduced to the adaptive sliding mode observer(SMO), which can remove the phase error between actual motor and model motor. Simulation and experimental results show that the proposed algorithm has strong robustness and speeds up the response of the system.

rotating coordinate system; dead time compensation;Lyapunov function;SMO; permanent magnet synchronous motor; rotor

TM301.2

A

1000-3983(2018)02-0012-05

2017-08-27

江苏省高校自然科学研究项目（14KJB470010）

黄亚军（1992-），硕士，研究方向为电力电子及电机控制技术。