基于优化参数的LS-SVM模型的股票价格时间序列预测

阚子良，蔡志丹

（长春理工大学 理学院，长春 130022）

股票预测涉及到投资者的经济利益，如何能提供较准确的股票预测一直是人们关注的热点问题。根据国内外专家学者的研究，当代金融数据越来越呈现出非线性的特征，传统时间序列的预测方法，比如AR、MA和ARMA等基于线性数据的模型，早已经不能适应需要。而神经网络[1］方法虽能提供较精确的结果，但是有网络模型和结构选择困难的缺点，容易陷入局部最小，训练速度慢，泛化能力差等现象。近年来支持向量机技术是神经网络之后出现的一种解决非线性问题的有效方法，属于机器学习[2-3］范畴，可以克服传统统计方法[4］和神经网络的很多缺点。

具体实验时，先运用最小二乘法改进运算效率和预测精度，考虑到支持向量机技术对参数的敏感性，又采用遗传算法优化支持向量机[5-10］的两个参数Gamma和γ。将某公司的107天的股票价格数据进行预测（含今日开盘价，收盘价，最高价，最低价，交易量，10日移动平均线，30日移动平均线和RSI）。将次日的收盘价为输出，利用主成分分析法提取20个变量中累积贡献率大于95%的变量为输入，训练模型并得出测试数据的预测值，对比模型参数优化前后的预测效果，从而对该改进算法进行分析。

1 股价预测模型的原理

1.1 传统支持向量机的基本原理

支持向量机是针对解决两种类别的分类问题而提出的。第一种是线性可分问题。设训练数据：x1，x2，...，xn，x∈Rn。

分类超平面最常见的表达式如下：

将训练数据和标签集转换为这样的形式：(x1，y1)，...，(xn，yn)，x∈Rn，y∈{+1，-1} 。于是激活（传递）函数可定义为：

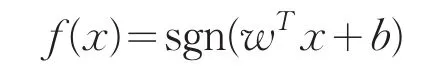
sgn表示符号函数，对应分类标签，函数只有两个输出值-1和+1。wTx+b=0是要寻找的最大间隔超平面。

训练样本为线性不可分时，加入正松弛变量ξi，i=1，2，...，n和惩罚因子C，原始问题为：

经过同样的推导过程，对偶优化问题为：

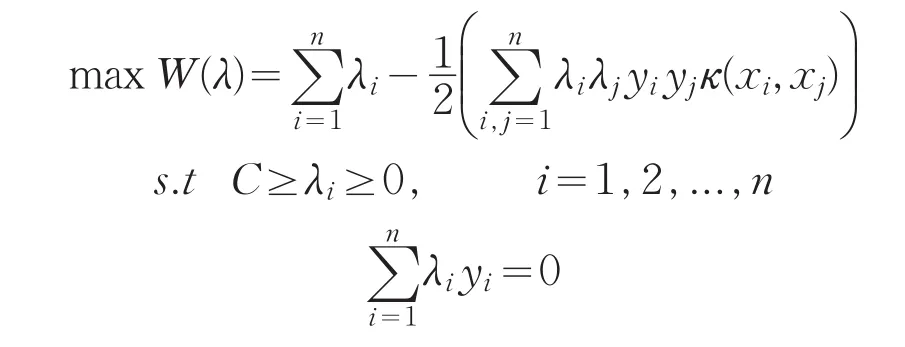
1.2 基于PCA-GA方法的参数寻优过程[11-12］

由于采集得到的股票数据的维数有20个，维数过大，故采取基于PCA去噪的参数寻优最小二乘支持向量机，主成分分析（PCA方法）是1901年由皮尔逊引入，1933年霍特林发展了该理论。主成分分析的就是将具有一定相关性的多个变量，组合成为一组相互无关的综合变量，进而代替原变量。具体预测步骤如下：

（1）下载样本数据集，归一化处理初始数据集。

（2）应用主成分分析法，提取累积贡献率达到90%以上的主成分作为输入变量。

（3）选取训练样本和测试样本。

（4）不通过参数的寻优对样本进行训练。再通过GA优化训练样本的参数，并进行回归训练。

（5）将测试样本输入训练好的LS-SVM和SVM回归模型中，输出预测结果，计算预测精度和拟合优度，比较优化前后的预测效果。

2 股票价格的预测及结果分析

2.1 样本的选取和预处理

由于最小二乘支持向量机的训练需要样本量足够大才能保证预测精度达到一定水平，在统计软件上提取了某公司的107天的股票价格，行变量为日期，列变量为今日的开盘价，收盘价，最高价，最低价，交易量，10日移动平均线，30日移动平均线和RSI。每列归一化后，将第二日的收盘价作为输出，用主成分分析法提取20个变量，累积贡献率95%以上的变量作为输入变量。考虑到训练样本应多于测试样本，前100天的数据应为训练样本，剩下的7天为测试样本。

2.2 对比方式

为了清晰地展现出优化前后的模型的效果差异，通过分析模型在计算机运行的时间长短，模型的均方误差，相关系数，画出期望输出和预测输出图，以及误差图，验证遗传算法优化最小二乘支持向量机参数可以极大提高模型的预测精度。

利用所建立的模型对股票数据预测后，为了解预测效果的好坏，即对预测的结果进行检验。现采用计算实际值与预测值的均方误差MSE来评价模型的好坏。MSE越小，说明预测精度越高，模型越好，反之，则越差。比较几种模型对相空间重构后的两组数据预测的MSE，分析对比出模型间的差异，以及优化的效果。

其中，e为实际值与预测值的差。

表1 各模型的参数与预测效果

2.3 实证研究过程

（1）预处理从同花顺股票软件下载的数据后，建立4个模型预测股票价格的开盘价，分别是原始的PCA-LS-SVM和基于GA算法、PCA的LS-SVM以及基于PCA的原始SVM和基于PCA-GA的SVM。从这四个模型看遗传算法是否能提高LS-SVM和SVM的预测效果。

（2）在Matlab中采用PCA提取累积贡献率大于95%的变量，利用计算机对变量进行主成分分析之后，得到最好的5个主成分，第一个主成分的贡献率约为65.93%，而这5个主成分的累积贡献率为99.14%。其次，建立原始的PCA最小二乘支持向量机模型。然后，通过实验实现基于GA算法、PCA的最小二乘支持向量机的预测过程，根据第1步的结果，利用遗传算法训练具有5个变量的新训练样本，得出其优化的参数g和γ。接着，将这两个参数代入到样本的训练之中，利用训练好的模型进行预测。SVM模型按同样的步骤进行。

（3）比较这两个模型的预测效果。运用MSE指标判断预测好坏，依据实验过程，总结出表1。

2.4 实证结果分析

可以从表1看出，经过遗传算法的参数优化后，无论原始的支持向量机，还是最小二乘支持向量机，其预测的均方误差都极大降低了，这证明了遗传算法的有效性和适用性；另外，4个模型中，均方误差最小的是基于PCA-GA的LS-SVM模型，其次是基于PCA-GA的SVM模型，说明了LS-SVM比SVM效果更好；鉴于高斯核比其他核函数具有更大的优势，实验均采用高斯核作为核函数。

现利用软件得出基于PCA-GA的最小二乘支持向量机模型在测试样本中的预测结果，如图1所示；预测结果图有上下两条线，上面的线是实际值，下面的线是预测值。可以看出，这两条线的走势基本一致，误差大小在2.5以内。

图1 基于PCA-GA的LS-SVM预测图

3 研究结论

通过利用多种模型对股票的收盘价进行预测实验，从实验的解决问题的过程和预测结果中，总结出如下的结论：

支持向量机模型可以仅仅利用很少的数据就能得出比较精准的预测结果。而且训练样本最好取距离测试样本较近的数据。

训练样本取太多，会导致模型泛化能力差，在训练样本内误差小，但在测试样本内会误差较大。

遗传算法对最小二乘支持向量机的参数的优化能极大提高建模的速率，还能使预测精度大大提升。这说明组合预测方法较单一的预测更有效。

机器学习作为股票等金融数据预测的有效方法，一方面大幅度地提升了分析处理这类数据的能力，另一方面还降低了成本。这种方法同样适用于其他复杂类型数据的预测。

[1]宋玉强.人工神经网络在时间序列预测中的应用研究[D］.西安：西安建筑科技大学，2005.

[2]孙翔侃，白宝兴.基于机器学习的NAO机器人检测跟踪[J］.长春理工大学学报：自然科学版，2016，39（2）：116-119.

[3]朱成璋.基于机器学习的时间序列预测关键技术研究[D］.长沙：国防科学技术大学，2014.

[4]Xiao QK，Xing L，Song G.Time series prediction using optimal theorem and dynamic Bayesian network[J］.Optik-International Journal for Light and Electron Optics，2016，127（23）：11063-11069.

[5]梅倩.LS-SVM在时间序列预测中的理论与应用研究[D］.重庆：重庆大学，2013.

[6]王鹏，高铖，杨华民.基于边分类的SVM模型在社区发现中的研究[J］.长春理工大学学报：自然科学版，2015，38（5）：127-130.

[7]梁礼明，钟震，陈召阳.支持向量机核函数选择研究与仿真[J］.计算机工程与科学，2015，37（6）：1135-1141.

[8]郭小溪，李刚，闫伟杰.基于遗传算法整定PID的自主潜器深度控制[J］.长春理工大学学报：自然科学版，2010，33（3）：37-39.

[9]陈伟根，滕黎，刘军，等.基于遗传优化支持向量机的变压器绕组热点温度预测模型[J］.电工技术学报，2014，29（1）：44-51.

[10]韩敏，许美玲，穆大芸.无核相关向量机在时间序列预测中的应用[J］.计算机学报，2014，37（12）：2427-2432.

[11]邵小健.支持向量机中若干优化算法研究[D］.青岛：山东科技大学，2005.

[12]毕建新，张志春，李小波.基于遗传算法的航空装备预防性维修优化研究[J］.长春理工大学学报：自然科学版，2011，34（03）：62-65.