机载稳定平台的神经网络PID控制

尹敬莹，杨成禹

（长春理工大学 光电工程学院，长春 130022）

机载稳定平台由于其能够测量平台姿态变化，保持平台的动态姿态稳定，隔离载体扰动使得载体上的仪器设备保持相对稳定，因此被广泛运用。由于载机在飞行过程中会受到风速、气流、风向变化等因素的影响，使得飞行姿态发生改变从而影响航拍质量，故而需要为机载相机提供一个稳定平台来隔离载机扰动，使其视轴与地理坐标保持相对稳定。通过对机载稳定平台的控制使机载相机始终处在一个相对稳定的状态进行拍摄确保航拍质量。

未经修正的平台系统稳态误差较大，且动态性能差，无法满足平台的稳定要求。随着控制理论和计算机技术的发展，由于数字控制器可以避免模拟控制器电路结构复杂和自身漂移的缺点，所以在平台控制中使用数字控制器已成为一种趋势，并且把现代控制理论应用到实际控制系统中，从而可以对系统更加精确的控制[1］。在稳定平台控制中常选用PID控制，但是由于机载稳定平台是非线性时变控制系统，PID控制对机载稳定平台的有效控制不足，提出神经网络PID控制并对稳定平台进行控制及仿真。

1 稳定平台结构

由于载机的飞行姿态变化分为横滚和俯仰两个方向，所以采用两轴稳定平台结构。其结构如图1所示。

图1中1为俯仰力矩电机，2为稳定平台俯仰框，3为水平仪，4为稳定平台横滚框，5为速率陀螺，6为基座，7为横滚力矩电机。其中速率陀螺用来稳定感知平台两个方向上的角速度信号，水平仪用来感知稳定平台两个方向上相对于水平位置的角位移信号。通过对电机负载的角速度和角位置的控制从而实现对平台的稳定控制[2］。

图1 双轴稳定平台结构示意图

稳定平台采用速度和位置的双闭环控制系统，其结构图如图2所示。内环为速度环，当平台受到外界扰动时会产生一定的角速度，控制系统会将检测到的信息反馈给速率元件，通过速率控制器进行调节补偿，然后控制信号驱动电机转动使其能够平衡掉外界干扰来保持平台的稳定；外环为位置环，当外界扰动使平台相对地面有一定的倾斜角度时，位置控制器会根据平台倾斜角度的变化量作为控制量，经速率控制器来驱动电机，使平台往相反方向倾斜，直至平台角度与初始角度相同为止，这样方能确保平台处于稳定状态。

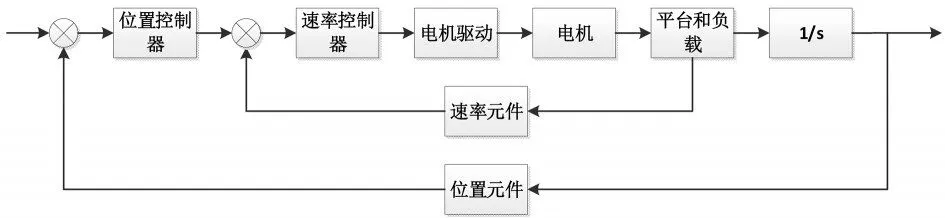
图2 稳定平台控制系统结构图

2 PID控制

PID控制系统由控制器和被控对象组成，其结构如图3所示。

图3 PID控制系统框图

其传递函数为：

式中，KP为比例系数，Ti为积分时间常数，Td为微分时间常数。

由于PID控制的控制效果是由比例，积分及微分环节三个环节相互协调影响，且PID是线性控制器，主要是利用PID控制器的参数调整，使稳定平台的稳定性达到目标要求。PID参数的整定依赖于经验，通过不断地调试来获得一个较为合理的PID参数以达到系统的要求。PID参数的整定决定了PID控制效果。在机载稳定平台系统的控制中，由于机载，稳定平台控制系统的参数会随时间及飞行姿态变化而PID控制难以自动调整参数以适应载机飞行姿态的变化，PID控制机载稳定平台系统不具有良好的稳定性及控制精度[3］。所以需要对机载稳定平台的PID控制进行改进以获得更好的控制效果。

3 神经网络

神经网络是模仿生物神经系统构成的处理模型，由许多并行运算的神经元组成，每个神经元可以连接多个输入，每个连接通路对应一个权系数。神经网络通过使用学习算法不断修改权系数从而实现调整网络输出，使网络的输出更符合要求。

神经网络的学习方法是指其将信息由输入层逐层传递至输出层输出，若输出不能达到期望值时，将误差信号反向传回，通过修改各层的参数来减小误差信号，再进行信息的正向传播，将信息的正向传递和误差的反向传递反复循环进行，直至误差小于给定值为止。神经网络的主要目的是使网络输出的误差达到最小。三层神经网络结构如图4所示。

图4 三层神经网络结构

如图4所示，x1，x2，…，xn是网络的输入，y1，y2，…，yh是隐含层的输出，z1，z2，…，zm是输出层的输出，t1，t2，…，tm是目标输出，隐含层到输出层的传递函数为f，输出层的传递函数为g。于是可得：

式中，yi代表隐含层第j个神经元的输出，ω0j=θ，x0=-1。输出层第k个神经元的输出zk：

此时实际输出与目标输出的误差为：

接下来就是通过调整权值使得ε减小。

神经网络不需要精确的数学模型、容易实现并行计算、擅长从输入输出中学习、具有非线性映射能力等特点。将其与PID控制相结合能够弥补PID控制的不足，使得机载稳定平台的控制更有效[4］。

4 神经网络PID控制

将神经网络和PID相结合得到的控制方法即神经网络PID控制（PIDNN）。该控制方法既具有神经网络和PID控制的优点，又克服了传统PID控制在非线性时变系统中控制效果差的缺点[5］。

由于机载稳定平台是单变量控制系统，所以对该系统的神经网络PID控制构建一个具有2个输入层，3个隐含层和1个输出层的三层前向神经网络[6］。3个隐含层分别为PID的三个参数即比例系数，积分系数，微分系数。结构如图5所示。

图5PIDNN结构图

在机载稳定平台的PIDNN控制中已经确定了输入层，隐含层，输出层及各层节点数，然后进行各层初始权值的选取。通过采样可以获得目标函数和输出函数，从而可计算出误差[7］。初始权值的选择不同则会影响PIDNN的控制效果。通过对输入层到隐含层权值的不断修正来对PID三个参数进行整定，修改隐含层至输出层的权值获得更好的控制效果。神经网络PID能利用神经网络的学习能力对随系统改变对PID参数进行整定，使其能有效控制机载稳定平台。

5 稳定平台PIDNN控制及仿真

由图2稳定平台控制系统结构图可以得到PIDNN控制结构，如图6所示。

图6 PIDNN控制结构图

其中θ0是输入角，θ1是输出角，KPWM为放大系数，Ra为电机电阻，T1为电气时间常数，Tm是电机时间常数。Ce是电机反电动势系数，Kf是反馈常数。

通过对系统结构框图的等效变换，可得系统的传递函数为：

对稳定平台PIDNN控制系统进行MATLAB仿真。设比例元和微分元的隐含层输入初始权系数为1，积分元的隐含层输入初始权系数为0.1，隐含层至输出层连接权系数初始值为0.1，100个采样点，采样步长为0.1，目标函数为：

其中，r(k)为理想输出，y(k)为实际输出。

若将载机运动看作正弦信号进行处理，则PID控制的误差曲线如图7所示，PIDNN误差曲线如图8所示。从图7中可以看出PID的误差较大且不稳定，PIDNN的误差小于0.008rad能够保证系统具有良好的稳定性。PIDNN比PID具有更高的精度和稳定性。

图7 PID误差曲线

图8 PIDNN误差曲线图

6 结论

由于PID控制算法简单，可靠性高，常被用于稳定平台的控制系统中。但是PID控制对非线性时变系统有效控制不足，而神经网络具有自适应、自学习能力，将二者相结合形成的神经网络PID控制利用神经网络的特点弥补PID控制的不足，在机载稳定平台的非线性时变控制系统中可以根据系统的运行状态，通过自身学习，找到最优控制下的PID三个参数，使系统具有良好的控制效果。通过仿真可以证明，机载稳定平台的神经网络PID控制具有较高的精度和稳定性。

[1]田礼.机载两维位置稳定平台控制系统设计与实现[D］.成都：电子科技大学，2016.

[2]张振东，徐涛，李博，等.航空相机稳定平台控制算法设计及其像移补偿[J］.电子技术应用，2012，38（09）：24-27.

[3]高富强，李萍，张磊敏，等.基于BP神经网络整定的PID控制及其仿真[J］.山东陶瓷，2017，40（03）：27-31.

[4]程森林，师超超.BP神经网络模型预测控制算法的仿真研究[J］.计算机系统应用，2011，20（08）：100-103，180.

[5]王连明，葛文奇，谢慕君.陀螺稳定平台速度环的一种神经网络自适应控制方法[J］.光电工程，2001，28（04）：9-12.

[6]曾军.神经网络PID控制器的研究及仿真[D］.长沙：湖南大学，2004.

[7]任子武.基于神经网络的参数自整定PID控制算法研究[D］.哈尔滨：哈尔滨理工大学，2004.