基于LMS算法的光纤振动预警系统降噪技术研究

张叶浩，衣文索，崔光磊，王家宁

（长春理工大学 光电工程学院，长春 130022）

分布式光纤振动预警技术集传感和传输于一体，可同时探测物理量的空间分布信息和时变信息，具有抗电磁干扰、体积小、成本低等无可比拟的优势，因而极适合应用于监测油气管道、输水管道、军事区域和边界国界等大范围实时预警系统中[1-4］。光纤振动预警系统通常采用基于光纤干涉仪的干涉型系统，其特点是灵敏度极高、易于实现、无盲区、实时性好，具有很好的实用和经济价值[5］。

振动波会引起传感光纤特征参量改变进而调制到光纤内光信号的相位中，然而在工程应用中，由于干涉光相位调制信号的灵敏度极高，极易受两种噪声干扰，一是由光纤散射光噪声、干涉偏振噪声和检测电路噪声组成的固定频带加性低频本底噪声，另一种是特性随环境时变的加性环境噪声[6］。前者可采用固定频率的滤波器，而后者相对复杂，在恶劣且不断变化的环境条件下，若振动信号本身能量较小，引起光相位信号将湮没于噪声中，振动信号信噪比将低于阈值，其一方面引起系统误报，另一方面，由于入侵信号定位技术普遍采用互相关时延估计算法，其定位精度降低取决于两路信号的相关性[7］，低于噪声水平的振动信号相关程度极低，无法满足定位需求，制约了干涉型光纤传感系统的发展。

因此，设计针对复杂环境噪声的降噪器是预警系统工程应用的关键技术之一。区别于通常的滤波场合，自然环境可视为参数时变的噪声信号，若使用固定指标的频域滤波器或空域滤波器对本系统信道进行均衡，由于偶发信号噪声混频现象与低信噪比，滤波结果难以满足工程需求，且因难以估计噪声的先验知识而限制了维纳滤波与卡尔曼滤波的应用。为解决上述问题，本文设计基于LMS算法以及其改进型算法的自适应噪声抵消器作为信号识别定位前的预处理单元。无论是平稳信号或是非平稳信号，自适应滤波算法都能明显提升信噪比且具有良好的性能指标[8，9］，当噪声是未知或者变化的信号时，自适应滤波器能够识别并跟踪这种变化，从而增强系统识别定位精度，特别适合环境噪声缓慢时变的光纤振动预警系统。

1 光纤预警系统原理与信号特征

1.1 系统结构

光纤振动预警系统基于双马赫曾德干涉仪，其等效结构图如图1所示，工作过程为：激光二极管发出1550nm窄带激光经过单向光学隔离器后经过3dB耦合器C1等功率分成两束光。一束沿顺时针进入光纤环行器R1后进入3dB耦合器C2等功率分成两束光，分别进入传感光纤臂1与参考光纤臂2，然后光臂中的传感光进入3dB耦合器C3合束并产生干涉效应，即该干涉光强信号中含有振动信号与噪声信号，再经光纤环行器R2进入光电探测器转化为电压信号，最终经过放大、A/D转换后进入上位机分析处理。同理，耦合器C1分出的另一束光沿逆时针进入光纤环行器R2再经过3dB耦合器C3后在耦合器C2处产生干涉，然后经由光纤环行器R1进入光电探测器最终同样经过调理后进入上位机分析处理。

图1 光纤振动预警系统结构图

1.2 光纤振动预警系统相位调制原理

由图1中传感光纤臂1与参考光纤臂2构成的传感光路预埋在预警目标区域土壤中数十厘米，实时检测由管道爆裂、人为挖掘或车辆进入预警区等行为引起的振动信号，显然光纤也受到风雨冲击等环境振动。振动信号通过光纤的调制效应（如：弹光效应、热应变效应等）使光纤折射率、纤芯长度、纤芯内径发生变化，进而导致光在光纤中传输时相位改变，即对光波相位的调制。

设光纤长度为L，折射率为n，直径为D，光波通过光纤的相移Δφ为：

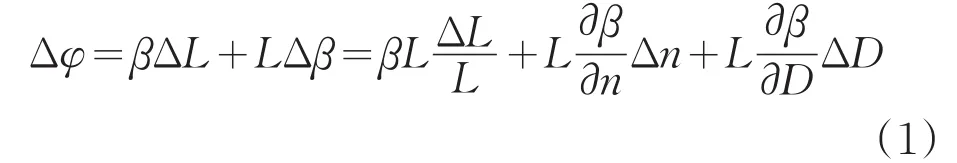
其中，β为光纤传播常数，可近似表示为光纤折射率和直径的函数。式（1）三项分别表示：光纤的弹性形变致使其长度变化所引起的传输光相位变化、弹光效应致使传感光纤折射率变化所引起的相位变化、泊松效应导致光纤纤芯直径变化所产生引起的相位差。可采用应变力场下的材料相对介电抗张量的变化Δβij来描述式（1）中前两项，第三项比前两项要小两三个数量级，可以略去，代入β=nk0，可得：

其中，k0=2π/λ0为传播常数，Pij为四阶弹光张量，εi为光纤各向应变。

可见，Δφ可以看作时间t的函数，系统中Mach Zehnder干涉仪利用光的干涉原理将函数Δφ(t)转换为光强信号，即

其中，I0表示光强，φ0为初始相位。

通过光电检测电路将上述光强信号I(t)转化为电压信号，再经由放大、A/D转换后进入上位机解调处理，即可识别与定位该光纤沿线上的振动信号，进而实现利用光纤实现监测和预警的效果。实际中Δφ(t)也同时包含自然环境干扰引起的相移，使系统产生误报漏报，严重影响系统稳定性。

1.3 噪声信号传输特征

基于上一节分析，自然环境振动作为时变随机噪声调制在式（2）中的φ(t)中，有：

其中，φn(t)为自然环境引起的光波相位噪声，φv（t）为待测预警信号。

严格来说φn(t)包含非平稳随机过程，由于自然环境变化相对缓慢，工程上常近似将短时间内的φn(t)视为平稳信号每隔固定时间对参数进行更新。不妨设某时间段tk的起始时间τ0处仅检测到噪声φn0(t)，tk结尾时间τ1处检测到包含噪声的预警振动信号φ(t)=φv(t)+φn1(t)，根据上述近似，噪声φn0(t)与φn1(t)的互相关系数ρn0n1、预警振动信号φy(t)与噪声φn1(t)的互相关系数ρyn1满足如下条件：

短时间内环境噪声φn(t)自相关程度很高，属于窄带随机噪声，因此可利用已检测到的振动预警信号产生前一时刻噪声的统计特征近似振动预警信号产生时噪声的统计特征。

2 自适应噪声抵消原理

2.1 自适应滤波结构

自适应噪声抵消技术建立在目前已广泛应用于数字信号增强、未知系统辨识与系统状态预测等领域的自适应滤波技术的基础上，通过多引入一路参考噪声作为辅助输入从而获取其统计特征，据此实时调整滤波器各抽头权参数以跟随这种变化，继而系统可完全抵消输入信号中的噪声成分，完成最优降噪过程。整个适应过程无须人为参与，系统根据预先设定的某种自适应控制算法准则主动完成权参数校正，特别适合全天候预警的光纤传感系统。

自适应滤波器包含IIR（无限长单位脉冲响应）型与FIR（有限长单位冲激响应）型两种结构，工程上为了追求系统稳定性，通常采用FIR型横向结构滤波器，也称抽头延迟线滤波器，其完整结构图如图2所示。

图2 横向结构自适应滤波器原理图

自适应滤波器由自适应控制算法与横向滤波器两部分组成，包含单位延时器、乘法器与加法器三个基本运算单元。每个横向输入信号x(n)都对应一个期望信号d(n)与一个输出信号y(n)，自适应控制算法输入参数，即误差信号e(n)表达式为：

横向滤波器中x(n-t)是n时刻输入信号x(n)延迟t个单位后的结果，所有输入抽头组成了滤波器的输入向量X(n)=[x(n)，x(n-1)，…，x(n-M+1)]T，总抽头个数（M-1）为滤波器的阶数。其中，乘法器的系数Wt(n)称为抽头权值，总计M个抽头权值组成了滤波器的权向量W(n)=[W0(n)，W1(n)，…，WM-1(n)]T，由此可推导输出信号y(n)的向量表达式为：

本文采用的自适应噪声抵消器基于上述结构，设光纤振动预警系统有预警振动信号为s(n)，同一时段有环境噪声n(n)，系统只需将光电探测器所接受到的包含部分环境噪声的振动预警信号作为图2自适应滤波系统的期望信号，并且将该时段曾收集到的纯噪声信号作为其输入信号，即：

s(n)、n(n)与n0(n)之间的相关系数满足式（5）与（6），噪声抵消器将根据自适应控制算法受到e(n)的控制调制使输出y(n)跟踪d(n)中的与n(n)高度相关的n0(n)，于是根据式（7），e(n)就越来越接近于预警振动信号s(n)。因此由上述方式组成的自适应噪声抵消系统能够很好的滤除噪声，输出高信噪比的振动信号。

2.2 自适应控制算法

当光纤振动预警系统中环境噪声信号的统计特性未知或变化时，自适应噪声抵消器能够根据e(n)调整权参数向量W(n)以满足某种最佳准则，每种最佳准则对应有独特的自适应控制算法。目前工程上应用最广的是以输出信号与理想信号的误差平方均值尽量小为基准的最小均方误差准则（Minimum Mean Square Error，MMSE），采用这一准则的最小均方（Least Mean Square，LMS）算法也成为自适应噪声抵消器中的标准算法。

LMS算法属于梯度最速下降法，因其算法复杂低、易于实现、无须人为监督等优点非常适合全天候实时监控的光纤振动预警系统，而其缺点是收敛速度一般且受输入信号统计特性影响。LMS算法包含一下两个基本过程：

（1）滤波过程。根据有输入向量X(n)时噪声抵消系统的输出y(n)与此时期望d(n)间的差值，计算出误差e(n)。

（2）自适应过程。根据误差e(n)，以使E[e2(n)]达到最小为基准来调整滤波过程中权参数向量W(n)。

二者共通组成图1中的闭环反馈结构。

自适应过程中权参数向量更新是依据上一时刻权向量与均方误差性能平面梯度之差决定，即

式中，μ称作自适应步长，∇(n)是均方误差函数E[e2(n)]的梯度，即：

在通常的最速下降法中计算出E[e(n)x(n)]非常复杂[10］，如果用瞬时值e(n)x(n)对E[e(n)x(n)]进行估算，得到梯度近似值的表达式：

用该梯度近似值代替最速下降法中梯度真实值∇(n)，代入式（11）得：

上式即为LMS算法的权更新迭代式，可见LMS算法用一个随机梯度值近似逼近难以计算的理论梯度真值，十分简明高效。

2.3 LMS算法性能指标

自适应步长μ是保证反馈结构稳定性，调整收敛速率的重要参数，必须满足如下条件：

其中，Pin为输入信号功率，此时算法收敛。可见滤波器阶数通过限制自适应步长的取值从而影响滤波结果。

在要求实时性好的光纤预警系统中，自适应学习过程的收敛速率是算法是否可工程应用的关键参数之一，收敛时间常数可表示为：

其中，λk为第k个输入信号自相关矩阵Rk的最大特征值。可见时间常数与自适应步长成反比，步长越小，收敛速率越慢。

由于LMS算法采用随机梯度值代替梯度真值，必然包含噪声，引入失调系数γ来表示真实性能与最佳性能间的稳态误差，其近似表达式为：

其中，λav为全体λk的均值，τmse，av为全体τmse的均值。可见失调与自适应步长成正比，即稳态误差随步长变小而降低。

在保证系统稳定性与算法收敛性的前提下，优先追求算法效率时，系统滤波效果会因此下降，反之若追求最优滤波结果，算法收敛速率与时间复杂度将难以令人满意，工程应用时通常多次实验来选取最合适系统的自适应步长μ。

2.4 变步长LMS算法

为解决上述矛盾，可使自适应步长μ以一定规律进行调整，即由固定步长μ改为时变步长μ(n)，其中应用最广泛的是归一化最小均方误差（Normalized LMS，NLMS）算法[11］。其步长函数μ(n)定义为：

虽然NLMS算法在输入包含大量有色噪声时的收敛速度和稳态误差都由优于固定步长LMS算法，但根据式（4）可知，NLMS算法在主要去噪对象为加性环境噪声时的收敛速率提升并不明显，且该算法更新步长函数μ(n)所花费的运算量将因光纤振动预警系统的高采样率而明显增加，降低系统响应速度。为了保持预警系统的时效性，可以使用一种基于符号函数的简化变步长算法（Hybrid LMS，HLMS）[12］，该算法将式（14）权值更新公式改写为：

其中，函数sgn[x］为符号函数。HLMS算法在基本保证性能的前提下简化了运算过程，且在输入信号非平稳时较LMS算法更为稳定。

3 仿真分析

3.1 对确定信号形式环境噪声的降噪性能仿真

光纤振动预警系统所检测的信号为振动周期信号，不失一般性，以两个不同振幅、频率与相位的正弦函数的和s(n)=sin（0.004n）+1.2cos（0.002n）作为待检振动信号。环境噪声可分为周期性的确定噪声与随机噪声，例如周边铁轨经过列车产生振动将以周期噪声信号的形式污染待检振动信号，用n(n)=sin（0.05n）模拟该噪声。实际中常遇到某一列车经过时突然驶来另一列车，为了模拟该噪声变化，将噪声信号n1(n)=1.2cos（0.08n）在t0时刻与n(n)叠加。

设d(n)为包含环境噪声的待检振动信号，e(n)为降噪结果，MSE=(e(n)-s(n))2为均方误差。根据工程经验并结合2.3节所述理论，为在满足精度的前提下使得收敛时间常数τmse与失调系数γ取得较好的折中，历经多次实验得到较为理想的步长μ=0.003。在Matlab R2016环境下，以上述条件对基于LMS算法噪声抵消器的降噪仿真结果如图3所示。

图3 基于LMS算法噪声抵消器对确定噪声的降噪结果

可以看出，降噪输出e(n)初期包含大量噪声，对应MSE值高于0.1，而在自适应噪声抵消器经过短时间训练后，e(n)快速趋于平滑，此时MSE值即降噪输出信号稳态均方误差已低于0.01，达到良好的降噪效果。在t0时刻叠加新的噪声信号n1(n)致使噪声特征突变，系统经历极短的调整后其MSE值仍低于0.01，降噪性能满足工程需求。

3.2 对平稳随机信号形式环境噪声的降噪性能仿真

自然界中复杂的环境噪声可认为是平稳随机信号且频谱范围广，常用理想加性噪声模型高斯白噪声wgn(n)来模拟该环境噪声，且光电探测模块中普遍存在热噪声和散粒噪声也属于高斯白噪声。实际中常遇到自然环境改变，如下雨、下雪等，导致噪声的统计特征产生改变，为模拟该变化，将另一高斯白噪声信号wgn1(n)在t0时刻与上述wgn(n)叠加，为控制变量其余参数保存不变，基于LMS算法的噪声抵消器对于高斯白噪声的降噪仿真结果如图4所示。

图4 基于LMS算法噪声抵消器对高斯白噪声的降噪结果

可以看出，降噪输出e(n)初期包含大量随机噪声，对应MSE值远高于0.1，同样，在自适应噪声抵消器经过短时间训练后，e(n)逐渐趋于平滑，此时MSE值即降噪输出信号稳态均方误差已低于0.1，即此时被高斯白噪声污染的信号已被很好的还原。在t0时叠加高斯白噪声信号wgn1(n)致使噪声显著加强，此时MSE仍低于0.1，降噪性能满足应用。

3.3 基于变步长HLMS算法的降噪性能仿真

变步长HLMS算法在LMS步长参数选择矛盾的前提下，算法复杂度也得到简化。为控制变量，采用与3.2小节一致的振动信号源、环境噪声与系统参数，基于HLMS算法的噪声抵消器对于高斯白噪声的降噪仿真结果如图5所示。

图5 基于HLMS算法噪声抵消器对高斯白噪声的降噪结果

相比于图4，图5中MSE值下降更快，在t0时叠加wgn1(n)后，MSE值更小且稳定。可见HLMS算法保证收敛速度的同时具有更好的鲁棒性，更适合实际应用。

4 结论

为了对因高灵敏度而易受环境噪声污染的光纤振动预警系统进行降噪处理，本文在分析其系统结构与信号调制原理的基础上，结合工程中普遍存在的噪声模型，采用基于LMS算法自适应噪声抵消器的降噪方案。经过建立自适应噪声抵消器结构、推导LMS算法原理、分析算法性能参数并提出采用更适合本系统的变步长HLMS算法、并结合Matlab仿真结果可以看出：该降噪方案在经历短暂时间收敛后，对不同环境干扰引起的随机噪声、确定噪声与特性时变的噪声均保持极低的稳态误差，有良好的去噪效果，且算法简单快速，具有工程应用前景。

[1]张晖，吕宏伟，冯进良，等.基于光纤振动传感器与FPGA的石油管道安防系统[J］.长春理工大学学报：自然科学版，2016，39（3）：116-119.

[2]廖延彪，黎敏.光纤光学[M］.北京：清华大学出版社，2013.

[3]Culshaw B，Kersey A.Fiber-optic sensing：a historical perspective[J］.Journal of Lightwave Technology，2008，26（9）：1064-1078.

[4]姜霁珊，江毅，刘达，等.基于双M-Z干涉仪的光纤周界防护系统[J］.光学技术，2015，41（3）：193-196.

[5]Li R，Wang X，Huang J，et al.Spatial-division-multiplexing addressed fiber laser hydrophone array[J］.Optics Letters，2013，38（11）：1909-1911.

[6]叶欣，罗洪，胡永明.干涉型光纤传感器低频信号检测技术研究[C］.全国光电技术学术交流会，2010.

[7]Lee B.Review of the present status of optical fiber sensors[J］.Optical Fiber Technology，2003，9（2）：57-79.

[8]张炳婷，赵建平，马淑丽.新的变步长LMS算法在系统辨识中的应用[J］.通信技术，2015，48（6）：653-656.

[9]李金龙.基于多尺度小波变换的改进型自适应滤波算法[J］.长春理工大学学报：自然科学版，2015，38（1）：143-147.

[10]张守勇.自适应回波抵消与噪声消除技术研究[D］.郑州：河南工业大学，2011.

[11]Weruaga L，Jimaa S.Exact NLMS algorithm with，μ-Norm constraint[J］.SignalProcessing Letters IEEE，2014，22（3）：366-370.

[12]石艳丽.基于DSP的自适应噪声抵消系统研究[D］.长春：长春理工大学，2008.