改进Smote算法在不平衡数据集上的分类研究

易 未,毛 力,孙 俊,吴林海

(1.江南大学物联网工程学院,江苏 无锡 214122; 2.江南大学商学院,江苏 无锡 214122;3.江南大学食品安全风险治理研究院,江苏 无锡 214122)

0 引 言

近年来，不平衡学习问题吸引了大量学术界和工业界的兴趣[1]。不平衡学习的根本问题是不平衡数据显著地降低标准学习算法的结果。大多数标准学习算法假设均衡类分布或具有相等的误判成本。因此，当面对复杂的不平衡数据集时，这些算法不能正确地反映数据的分布特征，从而使得结果精度不能令人满意。希望不同类别样本的数量是相等的，但是实际上在某些情况下不同类别样本数量通常是极端不平衡的，一类严重代表了另外一个类[2-4]。不平衡学习困难有2种解决方法，一是从算法上考虑，例如代价敏感[5]和集成学习方法[6]；二是对不平衡样本进行抽样然后再使用常用的机器学习算法。抽样有欠抽样(从多数类中抽取样本)[7-8]与过抽样(合成少数类样本)这2种方法。不平衡随机过采样算法随机复制少数集样本，最终使少数集样本数量与多数集样本数量相同，而Smote算法的基本思想是通过少数类样本的k个最近邻样本，合成新的样本再添加到数据集中，最终使少数样本与多数样本数量相同[9]。但是，Smote算法的主要缺点有：1)负类集合中的噪声负类样本参与新样本的合成，使得产生的新样本质量较差；2)没有对少数类样本进行区别性的选择，而是同等对待所有的少数类样本；3)生成新样本时，负类样本的k近邻可能是正类样本，这容易产生正负类边界模糊问题；4)合成样本仅在2个点的连线上产生，分布区域较小，分类器分类时易过拟合。

针对Smote算法的缺点，一些人对Smote算法提出了改进。董燕杰[10]提出Random-Smote算法，该算法对Smote算法的第4个缺点进行了改进，在样本点与2个近邻点所形成的三角形区域里面随机插值。王超学等人[11]提出了改进型Smote算法，该算法对Smote算法的第2个缺点进行了改进，使用轮盘赌算法来选择少数类集合中的少数类样本。Han等人[12]提出的Borderline-Smote算法，该算法对Smote算法的第1个缺点与第2个缺点进行了改进，仅仅只对在分类边界上的少数类样本过采样。Santos等人[13]提出了CB-Smote算法，该算法对Smote算法的第3个缺点进行了改进，生成新样本时的类别标签由该样本与其最近邻样本的类别标签共同决定。袁铭[14]提出了R-Smote算法，该算法对Smote算法的第3个缺点与第4个缺点进行了改进，在2个少数类样本上使用N维球面使生成的样本不在原样本与其近邻的直线上。古平等人[15]提出了SD-ISmote算法，该算法对Smote算法的第2个缺点、第3个缺点与第4个缺点进行了改进，根据近邻分布对少数类样本进行类别细分，对不同细分的少数类样本分别使用R-Smote与Smote算法合成新样本。

以上算法对Smote算法做出了许多改进，但总体分类性能还是稍显不足。因此本文利用删去噪音样本的少数类样本集簇心与不大于样本属性数的对应类别少数集数据，使用新的样本生成公式，提出一种新的改进型Smote算法—ImprovedSmote算法。

1 相关知识

1.1 Smote算法

Smote算法全称是合成少数类过采样技术(Synthetic Minority Oversampling Technique， Smote)，它的算法描述如下：

1)对于少数类Smin中每一个样本xi，以欧氏距离为标准计算它到全体样本集中其他的所有样本距离，得到其k个最近邻。

2)根据数据集不平衡比例设置一个采样倍率N，从少数集样本中循环选择样本，假设选择的样本为xi。

3)对于每一个选出的样本xi，对其k个最近邻中的每一个样本xold按照公式(1)构建N个新样本xnew：

xnew=xi+rand(0,1)×(xold-xi)

(1)

4)从新生成的少数集数据中随机剔除数据，直到新生成少数集数据个数等于原多数集与少数集数据个数之差，然后把生成的数据加入到原来的少数集Smin中。

1.2 R-Smote算法

Smote算法在生成新样本时，新样本分布区域较小，仅仅在线性空间上产生。因此，袁铭提出了R-Smote算法，它的算法描述如下：

1)对于少数类Smin中每一个样本xi，以欧氏距离为标准计算它到全体样本集中其他的所有样本距离，得到其k个最近邻。

2)根据数据集不平衡比例设置一个采样倍率N，从少数集样本中循环选择样本，假设选择的样本为xi。

3)对于每一个选出的样本xi，从其k个最近邻中随机选择1个少数类样本xold按照公式(2)～公式(4)构建新样本xnew：

Z1,j=xi,j-|xold,j-xi,j|

(2)

Z2,j=xi,j+|xold,j-xi,j|

(3)

xnew,j=xi,j+rand(0,1)×(Z2,j-Z1,j)

(4)

其中，xi,j代表样本xi的第j个属性。

4)xi与其生成的新样本的距离应该小于xi与xold的距离，即：

dist(xi,xnew)≤dist(xi,xold)

(5)

如果不满足公式(5)则跳转到步骤2。

5)生成的少数集数据个数等于原多数集与少数集数据个数之差时停止生成，并把生成的数据加入到原来的少数集Smin中。

1.3 SD-ISmote算法

Smote与R-Smote算法在新样本产生时并没有利用多数类样本的信息，古平等人提出了SD-ISmote算法，根据最近邻的情况对少数类样本进行不同处理方法。它的算法描述如下：

1)对于少数类Smin中每一个样本xi，以欧氏距离为标准计算它到全体样本集中其他的所有样本距离，得到其k个最近邻。

2)按照最近邻少数类样本个数把Smin细分为DANGER(少数类样本个数小于k/2)、SAFE(少数类样本个数等于k)、AL_SAFE(少数类样本个数大于k/2，小于k)集合。

3)统计DANGER，SAFE，AL_SAFE样本个数，得到ND，NS，NAL。在DANGER集上使用R-Smote算法进行过采样，采样数量为D×NS/(ND+NS+NAL)，其中，D为整体过采样数量。

4)在SAFE集上使用Smote算法进行过采样，采样数量为D×ND/(ND+NS+NAL)。

5)对于AL_SAFE集合，利用轮盘赌来选择样本。按照公式(6)计算每个样本的选择概率：

(6)

其中，sup(i)为AL_SAFE中样本最近k近邻少数样本数量。

6)选择样本后使用R-Smote算法生成新样本，并利用最近1分类判断最近邻是否为少数类。过采样数目为D×NAL/(ND+NS+NAL)。

7)合并DANGER，SAFE，AL_SAFE产生的新样本，并把生成的数据加入到原来的少数集Smin中。

2 ImprovedSmote算法

上文中提到R-Smote与SD-ISmote算法，分析它们的算法流程，首先会发现R-Smote算法在生成新样本之后还需要满足公式(5)，SD-ISmote算法在满足公式(5)的基础上还要满足新样本的最近1近邻必须为少数类。由于这2个条件的影响，R-Smote与SD-ISmote算法新样本产生的效率不高。同时SD-ISmote算法没有对Smote算法负类集合中的噪声负类样本参与新样本的合成，使得产生的新样本质量较差这个缺点进行改进。

针对以上问题，本文提出了ImprovedSmote算法。它的主要思想是：1)剔除少数数据集中的噪音数据，这改进了Smote算法的第1个缺点；2)在剔除噪音数据的少数数据集上使用k-means算法，使用簇心与对应类别的少数集数据生成新样本，这改进了Smote算法的第2个缺点与第3个缺点；3)新样本在簇心与对应类别的少数集数据形成的图形内部随机产生，这改进了Smote算法的第4个缺点，同时也改进了R-Smote与SD-ISmote算法新样本产生效率不高的缺点。

2.1 ImprovedSmote算法实现步骤

1)数据预处理，然后使用快速搜索与发现密度峰值聚类(Clustering by Fast Search and Find of Density Peaks，CFSFDP)算法求得聚类中心个数[16]。

(7)

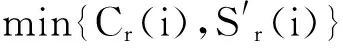
5)如果样本数量|Sr|≤a，则按照公式(8)生成新样本xnew：

xnew(i)=rand(min{Cr(i),Sr(i)}, max{

Cr(i),Sr(i)}), 1≤i≤a

(8)

6)重复步骤4和步骤5直到新生成的数据个数等于原多数类数据集个数与原少数类数据集个数之差。

7)输出平衡后的数据集。

2.2 ImprovedSmote算法流程

输入：原始数据集T，少数类数据集M，多数类与少数类样本数量之差D，根据CFSFDP算法得到的聚类中心个数k。

输出：平衡数据集T*。

1)对于数据集M上每一个少数集样本a，在数据集T(去除样本a)中使用KNN算法求其近邻，若其全部近邻是多数类别，则把a从M中删除，得到数据集M*。

2)在M*中使用k-means算法(k-means算法k值为聚类中心个数k)，得到k个簇心{C1,C2,…,Ck}与对应该簇心的所有少数集样本{S1,S2,…,Sk}。

3)计算少数集样本{S1,S2,…,Sk}的样本个数|S1|,|S2|,…,|Sk|。

4)合成所有的少数类新样本，过程如下：

for j=1:D

{n=rand(1,k)；

if |Sn|>样本数据属性个数b{

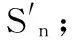
for i=1:b

}

else {

for i=1:b

x(i)=rand(min{Cn(i),Sn(i)}, max{Cn(i),Sn(i)})；

}

xnew=xnew∪x；

}

T*=T∪xnew；

5)输出T*。

2.3 ImprovedSmote算法复杂度分析

定义n为少数集样本数量，m为多数集样本数量，样本属性个数为b。ImprovedSmote算法流程步骤1中，计算少数集每个点之间的距离时间复杂度是O(bn(n+m-1)/2)，求k1个距离最小值时间复杂度为O(k1(n+m)n)，删除操作为O(1)，即步骤1总的时间复杂度是O(bn(n+m-1)/2+k1(n+m)n+1)=O(nm)。步骤2中，k-means算法的时间复杂度为O(Tk2n)，其中T为迭代次数，k2为k-means算法的分类数。一般地，T与k2比n小得多，因此k-means算法的时间复杂度可以简化为O(n)。步骤3中，时间复杂度是O(1)。步骤4中，若|Sn|≤b，时间复杂度为O((m-n)×b2)=O(m-n)，否则为O((m-n)×(b+b2))=O(m-n)。综上，ImprovedSmote算法时间复杂度为O(nm)。ImprovedSmote算法与Smote算法的时间复杂度基本相同。

ImprovedSmote算法空间复杂度取决于存储步骤1中少数集点与全体样本的距离。因此，ImprovedSmote算法空间复杂度为O(n(n+m-1)/2)=O(nm)，与Smote及其变种算法的空间复杂度基本相同。

3 实 验

本文实验所使用的数据集分别是german，yeast，pima，glass这4个数据集。这4个数据集来源于UCI Machine Learning Repository。其中german与pima这2个数据集都是二分类数据集。yeast选择第五类为少数类，其他合并为多数类。glass选择第七类为少数类，其他合并为多数类。具体描述如表1所示。

表1 不平衡数据集描述

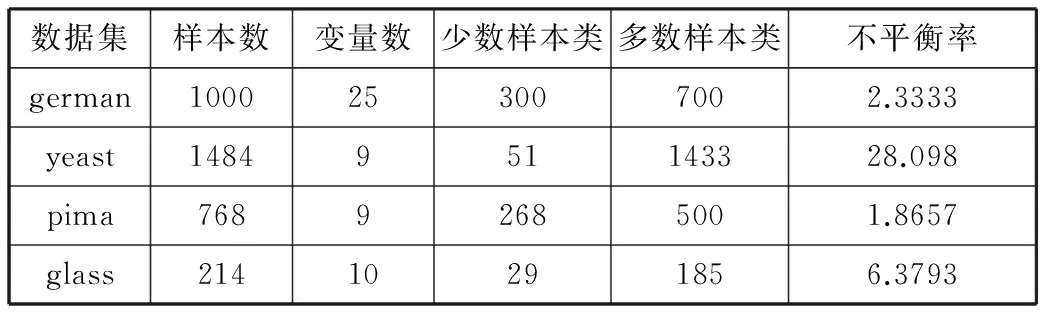
数据集样本数变量数少数样本类多数样本类不平衡率german1000253007002.3333yeast1484951143328.098pima76892685001.8657glass21410291856.3793

由表1可以看出每个数据集的样本数、少数样本数、多数样本数、所含变量数以及不平衡率。不平衡率是多数样本集与少数样本集数量之比，数值越大则该数据集的不平衡程度越大。

3.1 不平衡学习的评价方法

1)所需参数。

TP：正类正确分类数量。

FP：预测为正类但是真实为负类数量。

FN：预测为负类但是真实为正类数量。

TN：负类正确分类数量。

3) AUC值。AUC(Area Under Curve)被定义为ROC曲线下的面积，一般取值范围为0.5～1。使用AUC值作为评价标准是因为很多时候ROC曲线并不能直观地说明哪个分类器的效果更好，而作为一个数值，对应AUC更大的分类器效果更好[17]。

4) G-Means×AUC。由于G-Means与AUC的值都大时，对应分类器效果更好。本文采用G-Means与AUC乘积值来评价分类器效果。

3.2 ImprovedSmote算法近邻参数k的确定

KNN算法近邻参数k值的选择在判断少数集样本是否为噪音样本时特别重要，本文使用二分类数据集，因此本文将选择1，3，5，7，9，11这6个1～11之间的奇数作为k的值，通过对比ImprovedSmote算法过采样之后的G-Means×AUC值来确定最佳的k值。不同k值的ImprovedSmote算法在german，yeast，pima，glass数据集上的分类结果如图1～图4所示。

图1 不同k值在german数据集的分类结果

由图1可以看出，k=3时ImprovedSmote算法在german数据集使用C4.5和神经网络算法均取得最大的G-Means×AUC值。

图2 不同k值在yeast数据集的分类结果

由图2可以看出，k=3时ImprovedSmote算法在yeast数据集使用C4.5和神经网络算法均取得最大的G-Means×AUC值。

图3 不同k值在pima数据集的分类结果

由图3可以看出，k=3时ImprovedSmote算法在pima数据集使用C4.5和神经网络算法均取得最大的G-Means×AUC值。

图4 不同k值在glass数据集的分类结果

由图4可以看出，k=3时ImprovedSmote算法在glass数据集使用C4.5和神经网络算法均取得最大的G-Means×AUC值。综上所述，在接下来的实验中ImprovedSmote算法的近邻参数选择为3。

3.3 实验步骤

1)确定少数集以及对应的聚类中心个数。

对german，yeast，pima，glass数据集进行数据预处理，然后在每个数据集对应的少数集上使用CFSFDP算法，求得german，yeast，pima，glass少数集的聚类中心个数分别为5，2，5，1。即german，yeast，pima，glass少数集样本k-means算法k值选取为5，2，5，1。

2)使用Smote，R-Smote，SD-ISmote与ImprovedSmote算法过采样数据集数据。

3)使用C4.5决策树与神经网络(NN)算法分类。

在经过Smote，R-Smote，SD-ISmote与ImprovedSmote算法处理后的数据集上按照7:3的比例分为训练集与测试集，使用C4.5决策树与神经网络算法分类，最后将测试集的分类结果一一记录。

3.4 4种过抽样算法的实验结果与分析

在Smote，R-Smote，SD-ISmote与ImprovedSmote过抽样算法处理后的数据集上使用C4.5决策树与神经网络算法分类。4个测试集上的分类结果如表2～表5所示。

表2 4种过抽样算法在german数据集上的分类结果

评价指标分类方法SmoteR-SmoteSD-ISmote本文算法G-MeansC4.50.74990.75570.77090.7917NN0.69030.72050.77430.7900AUCC4.50.77620.77100.78520.8016NN0.75580.78400.83980.8708G-Means×AUCC4.50.58210.58260.60530.6347NN0.52170.56490.65020.6879

G-Means值越高，说明多数类与少数类上的分类精度均较高；AUC值越高，说明分类效果越好。G-Means×AUC值越高，说明分类器总体上的分类表现越好。从表2中可以看出，在german数据集上相较于Smote，R-Smote与SD-ISmote算法，ImprovedSmote算法在C4.5与神经网络分类算法下都能得到更高的G-Means与AUC值，所以其G-Means×AUC值也更高。

表3 4种过抽样算法在yeast数据集上的分类结果

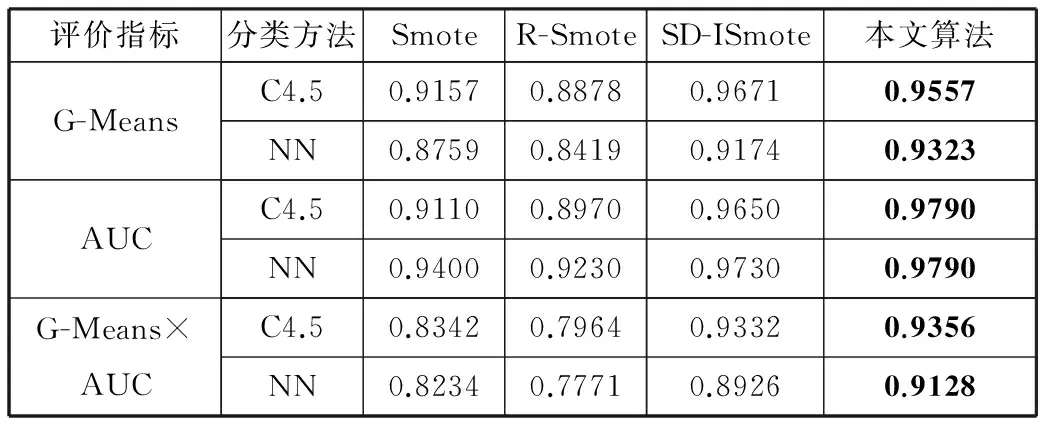
评价指标分类方法SmoteR-SmoteSD-ISmote本文算法G-MeansC4.50.91570.88780.96710.9557NN0.87590.84190.91740.9323AUCC4.50.91100.89700.96500.9790NN0.94000.92300.97300.9790G-Means×AUCC4.50.83420.79640.93320.9356NN0.82340.77710.89260.9128

从表3中可以看出，在yeast数据集上相较于Smote，R-Smote与SD-ISmote算法，ImprovedSmote算法在C4.5与神经网络分类算法下都能得到更高的AUC值。虽然ImprovedSmote算法的G-Means值在C4.5分类算法下比SD-ISmote算法低0.0119，但是G-Means×AUC值均为最高。

表4 4种过抽样算法在pima数据集上的分类结果

评价指标分类方法SmoteR-SmoteSD-ISmote本文算法G-MeansC4.50.73940.76930.77750.8047NN0.71740.72780.72720.7644AUCC4.50.78400.79700.81300.8220NN0.75700.81400.82200.8580G-Means×AUCC4.50.57970.61320.63210.6615NN0.54310.59240.59780.6559

从表4中可以看出，在pima数据集上相较于Smote，R-Smote与SD-ISmote算法，ImprovedSmote算法在C4.5与神经网络分类算法下都能得到更高的G-Means与AUC值，所以其G-Means×AUC值也更高。

表5 4种过抽样算法在glass数据集上的分类结果

评价指标分类方法SmoteR-SmoteSD-ISmote本文算法G-MeansC4.50.89760.94540.92690.9747NN0.94430.94550.96320.9829AUCC4.50.88300.92600.95400.9710NN0.98300.99300.98200.9940G-Means×AUCC4.50.79260.87540.88430.9464NN0.92820.93890.94590.9770

从表5中可以看出，在glass数据集上相较于Smote，R-Smote与SD-ISmote算法，ImprovedSmote算法在C4.5与神经网络分类算法下都能得到更高的G-Means与AUC值，所以其G-Means×AUC值也更高。

ImprovedSmote算法在实验数据集上G-Means×AUC值均较Smote，R-Smote和SD-ISmote算法高。ImprovedSmote算法与Smote，R-Smote和SD-ISmote算法相比： 1)剔除了少数集中的噪音数据样本，使得这部分样本不会生成新样本；2)使用簇心与不大于样本属性数的对应类别少数集数据生成新样本，对少数类样本进行了区别性的选择；3)参与合成新样本的样本都属于少数类，产生的新数据不会模糊多数类与少数类的边界；4)新样本在簇心与不大于样本属性数的对应类别少数集数据形成的图形内部随机产生，使得不仅产生新样本的分布范围更广，而且产生新样本的效率也高。综上所述，ImprovedSmote算法优于Smote，R-Smote和SD-ISmote算法，更加有效地增加不平衡数据集的少数类样本，从而提高分类器分类性能。

4 结束语

针对在不平衡数据集上有效地分类这个问题，本文提出了ImprovedSmote算法，该算法剔除了少数集中的噪音数据样本，使用k-means算法求得少数数据集的簇心，然后使用簇心和不大于样本属性数的对应类别的少数集数据生成新样本，这可以防止噪音数据样本产生新样本与新数据不会模糊多数类与少数类的边界。新样本在簇心与不大于样本属性数的对应类别的少数集数据形成的图形内部随机产生，增大了新样本的生成范围，减少分类器分类时易过拟合这种现象的产生。实验结果显示ImprovedSmote算法结合C4.5决策树与神经网络算法在实验数据集上的分类效果较Smote，R-Smote和SD-ISmote算法好。下一阶段将改进对应类别的少数集数据个数大于样本属性个数时的数据抽取方法，使生成的新样本分布更加合理。

[1] He Haibo, Garcia E A. Learning from imbalanced data[J]. IEEE Transactions on Knowledge & Data Engineering, 2009,21(9):1263-1284.

[2] He Haibo, Shen Xiaoping. A ranked subspace learning method for gene expression data classification[C]// Proceedings of 2007 International Conference on Artificial Intelligence. 2007:358-364.

[3] Kubat M, Holte R C, Matwin S. Machine learning for the detection of oil spills in satellite radar images[J]. Machine Learning, 1998,30(2-3):195-215.

[4] Pearson R, Goney G, Shwaber J. Imbalanced clustering for microarray time-series[C]// Workshop for Learning from Imbalanced Datasets II, 2003．

[5] Zhao Hong, Li Xiangju. A cost sensitive decision tree algorithm based on weighted class distribution with batch deleting attribute mechanism[J]. Information Sciences, 2017,378(C):303-316.

[6] Reddy M V, Sodhi R. A rule-based s-transform and ada-boost based approach for power quality assessment[J]. Electric Power Systems Research, 2016,134:66-79.

[7] 史颖,亓慧. 一种去冗余抽样的非平衡数据分类方法[J]. 山西大学学报(自然科学版), 2017,40(2):255-261.

[8] Yen S J, Lee Y S. Cluster-based under-sampling approaches for imbalanced data distributions[J]. Expert Systems with Applications, 2009,36(3):5718-5727.

[9] Chawla N V, Bowyer K W, Hall L O, et al. SMOTE: Synthetic minority over-sampling technique[J]. Journal of Artificial Intelligence Research, 2011,16(1):321-357.

[10] 董燕杰. 不平衡数据集分类的Random-SMOTE方法研究[D]. 大连:大连理工大学, 2009.

[11] 王超学,潘正茂,董丽丽,等. 基于改进SMOTE的非平衡数据集分类研究[J]. 计算机工程与应用, 2013,49(2):184-187.

[12] Han Hui, Wang Wenyuan, Mao Binghuan. Borderline-SMOTE: A new over-sampling method in imbalanced data sets learning[C]// Proceedings of 2005 International Conference on Advances in Intelligent Computing. 2005,3644(5):878-887.

[13] Santos M S, Abreu P H, García-Laencina P J, et al. A new cluster-based oversampling method for improving survival prediction of hepatocellular carcinoma patients[J]. Journal of Biomedical Informatics, 2015,58:49-59.

[14] 袁铭. 基于R-SMOTE方法的非平衡数据分类研究[D]. 保定:河北大学, 2015．

[15] 古平,杨炀. 面向不均衡数据集中少数类细分的过采样算法[J]. 计算机工程, 2017,43(2):241-247.

[16] Rodriguez A, Laio A. Machine learning. clustering by fast search and find of density peaks[J]. Science, 2014,344(6191):1492-1496.

[17] 杨明,尹军梅,吉根林. 不平衡数据集分类方法综述[C]// 第三届江苏计算机大会论文集. 2008.