离心压缩机叶轮防共振逆向设计方法研究

顾崇廉，张 帅，吴 奎，窦 磊

(太阳宫燃气热电有限公司，北京 100029)

离心式压缩机具有单机容量大、结构合理、运行可靠和占地面积小等优点，在工业中有着不可替代的作用，在冶金、化工和石油等行业有着重要的地位。随着压缩机不断的大型化、高速化，离心式压缩机的工作环境越来越恶劣。在压缩机中，叶轮是唯一的做功元件，一旦发生损坏会造成严重的后果，在叶片问题中，压缩机叶片的共振往往会造成很严重的事故；因此，判断压缩机叶轮的共振点，是压缩机叶轮投入使用之前的一项重要工作。

对于压缩机叶轮共振点的判断方法，最早有Campbell图法，但是该方法是用于判断单叶片的共振情况，在判断整圈叶片时有一定局限性，判断出的共振点可能是虚假共振点，会为之后的叶片使用造成不必要的麻烦。1972年，黄文虎教授提出的“三重点”调频理论[1-3]得到了广泛的认可，但是由于计算机计算能力的限制，使得此理论的使用受到了限制。2004年，随着计算机计算能力的提高以及有限元分析的发展，Singh等[4]提出了SAFT图法，在Campbell图的基础上，对共振点进行进一步判断，能够更准确地判断共振点。

本文通过对国外某叶片进行逆向工程，并且通过SAFT图的形式评估逆向叶片的可靠性，为叶片的逆向设计提供了很好的测试方法，促进了新产品研发以及加快先进透平机械国产化步伐。

由于模态分析的重要性，对于模态的振动规律前人也做了很多工作，杨猛等[5]针对涡旋压缩机进行了有限元分析，分析了叶轮的振动形态规律；孔祥强等[6]对制冷压缩机的模态进行了研究，探究了共振发生的规律，说明了对于叶轮模态规律分析的必要性。本文针对模态分析转换思路，从叶轮模态频率变化规律入手，初步探究叶轮的模态规律，为叶轮的模态分析提供参考。

1 整圈叶片共振条件理论

叶片是否发生共振与激振力是否做功有关，激振力做功不为零，即发生共振。

叶片旋转时的激振力可以使用傅里叶级数展开，得到N阶谐波的表达式为：

fN(θ,t)=FNsinN(ωNt+θ)

式中，FN为N阶谐波的振幅；θ为在轮盘上的角位置；t为时间；ωN为激振力的基频，即ωN=n/60。

第m节径的位移可以表示为：

ym(θ,t)=-Ymcos(ωmt+mθ)

式中，ωm是节径数为m的固有频率。

于是，第N个激振力成分fN(θ,t)在1个周期T内做的功为：

带入N阶谐波方程和m节径位移公式可得：

由上式可以看出，叶轮发生共振有如下2个条件：1)叶片固有频率等于激振力频率；2)节径数m=N。

2 某增压机叶片模型的获取及分析

2.1 叶轮来源

本文使用的叶轮为美国某公司生产的某型号增压机的离心式叶轮，叶轮实物图如图1所示。

图1 离心式叶轮实物图

叶轮采用便携式三坐标的激光扫描+尺寸测量的方法进行逆向，同时采用桥式三坐标的硬测头对叶片部位进行复检。便携式三坐标型号为FARO EDGE2.7(见图2)；该设备测量精度可达0.029 mm，每秒可取40 000个点，在叶轮表面采取致密的点云(见图3)。

图2 便携式三坐标测量仪

图3 三坐标测量的点云图

应用Geomagic Design X软件对点云数据进行后处理，将点云拟合成三角面片，再通过拉伸、回转和扫略等命令将其转化为三维实体。在逆向的过程中，根据叶片直纹面的特性，对其进行规律延伸，以达到对叶片缺失部位的修补。

叶轮3D建模后，再通过桥式三坐标将叶轮实体和3D模型进行对比测量，以保证逆向后的模型与叶轮实体间的偏差最小，最终得到叶轮的工程图，实现逆向设计。叶轮3D建模图形如图4所示。

图4 叶轮3D模型

2.2 逆向叶轮准确性分析

根据逆向得到的叶轮3D数据模型，应用最先进的NREC软件进行全流场的CFD气动分析，确保逆向后的叶轮能够完全满足原始工艺设计要求，并对其进行替代。所有输入数据均取自操作手册中的数据表。叶轮准确性分析如图5所示。模拟结果与实际的试验结果对比见表1。

图5 叶轮准确性分析

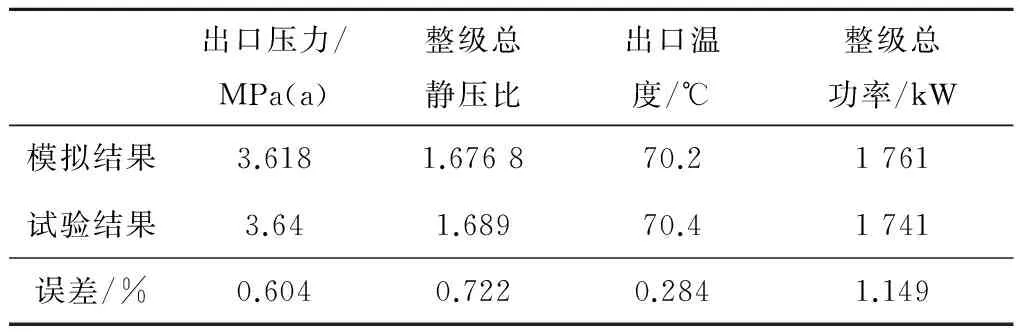
出口压力/MPa(a)整级总静压比出口温度/℃整级总功率/kW模拟结果3.6181.676870.21761试验结果3.641.68970.41741误差/%0.6040.7220.2841.149

由表1可以看出，模拟结果和试验结果基本符合，误差都保持在1%左右。通过这些计算可知，该逆向的叶轮在气动性能上对原叶轮完全具备替代条件，并满足原始的工艺设计要求，为下一步的模态分析打下了良好的基础。

2.3 叶轮模态分析

叶轮有16个叶片，工作转速为27 353 r/min，本次分析对模型进行简化，不考虑气流激振，只考虑转速和导叶带来的激振力。原机器中有12个导叶。使用workbench中的modle模块，进行网格的划分以及模态的分析，网格划分结果如图6所示。

图6 叶轮网格划分

图6为1/16叶轮，叶片使用单元为solid186六面体20节点单元，相对于四面体单元，其有着更加精确的计算精度。对于叶盘，由于对分析结果准确性要求不太高，则使用较易计算的solid187四面体10节点单元，这样可加快运算速度，节约时间成本。

考虑离心力对于固有频率的影响，模态计算应在离心力作为预应力的情况下进行，首先计算叶片的离心力，之后将离心力导入到模态计算中作为预应力，进行模态的计算。

为得到Campbell图，首先，依次计算转速0～27 535 r/min(额定转速)内，以4 000 r/min为间隔的多个转速的固有频率，在Campbell图中找到激振力和频率线的交点，从而找到可能的共振点；然后，通过绘制不同节径、不同模态下的频率图，并通过绘制速度线，评估Campbell图中的交点映射在SAFT图中的点是否满足m=N，从而更准确地评估叶片的共振特性。

3 结果分析

3.1 Campbell图和SAFT图的共振分析

3.1.1 叶轮模态分析

前3阶Campbell图如图7所示。根据SAFT图理论，首先应在Campbell图中判断可能的共振点，图7中过原点的直线为1倍和2倍激振频率，激振力来源为入口导叶，所以只考虑导叶激振力频率，根据Campbell图，找到激振力与固有频率的交点，交点转速为可能的共振点。

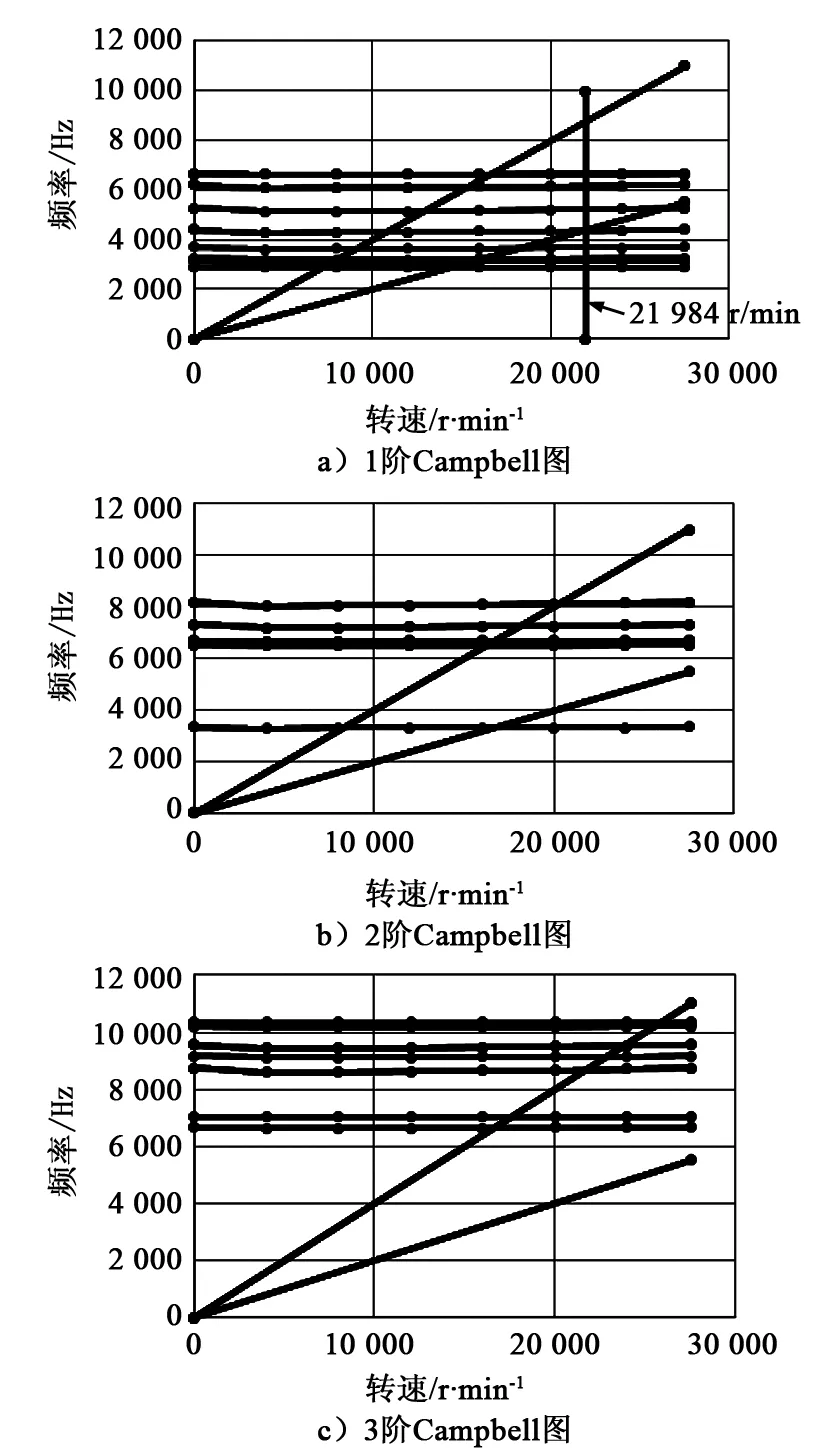
图7 前3阶Campbell图

图7中Campbell图过原点的斜线为激振力频率，其余的线为每阶不同节径下的固有频率。1阶前4节径模态图的示意图如图8所示。

图8 1阶模态图

图7中，在额定转速为27 535 r/min情况下，Campbell图中没有交点，因此无共振可能性，但是实际压缩机运行过程中，转速会有一定的波动，因此对于临近的交点的共振情况也应该进行关注，如在1阶Campbell图中转速为26 220 r/min处交点，则处于转速波动范围，但在2阶Campbell图中交点转速距离额定转速较远，则不需考虑。

下述使用1阶Campbell图中的交点对使用SAFT图进一步判断共振点的方法进行解释。

在本次分析的叶轮中，N=12，对于上文中的交点，已经保证了共振条件1，但是未保证共振条件m=N。

对于此叶轮，最大节径为8，N=12已经大于最大节径数，这种情况在SAFT图中称之为混淆，需要针对发生共振的节径数进行计算，公式为：

K=abs(nL-M)

式中，n=0,1,2,3…；L为叶片数；M为激振力频率。则发生共振的1阶激振力的节径数为abs(2×8-12)=4。SAFT图如图9所示。

图9 SAFT图

在4节径处，激振力频率为5 507 Hz，叶片的1阶和2阶固有频率分别为4 396.8和6 665.6 Hz，安全裕度分别为25.3%和17.4%，安全裕度较大，不会发生共振，即Campbell图判断的共振点为虚假共振点。

依照此方法可以判断之后的一系列共振点，为之后的工程实践提供很大的参考价值，对于离心式压缩机的运行启动有着很重要的指导意义。

3.1.2 SAFT图可靠性分析

为分析SAFT图分析模态的可靠性，在SAFT图中，依据SAFT图判断共振的条件，绘制共振速度线，即使转速线恰好与1阶4节径的固有频率线相交，如图9中的21 984 r/min线。此转速根据4节径处固有频率为4 396.8 Hz计算得出。

在SAFT图中，因为转速线与固有频率线有交点，且交点为导叶的1阶通过频率，按照SAFT图判断条件，则一定发生共振。

在Campbell图中的1阶Campbell图画出转速为21 984 r/min的转速线，如图7中1阶Campbell图所示。在Campbell图中可以明显发现，在4节径处，转速21 984 r/min下有共振点。

根据上述分析可得出，SAFT图判断的共振点一定是Campbell图中的共振点。

3.1.3 SAFT图优势分析

根据上述分析可明显看出SAFT图在整圈叶片分析上相对于Campbell图的优势，总结如下：1)可以排除虚假共振点，减少操作压缩机和设计压缩机叶片不必要的麻烦；2)可以根据SAFT图判断共振裕度，从而为压缩机的稳定性提供参考，防止事故发生；3)将Campbell图进行优化，使得Campbell图能够反映更多的节径信息，一定程度上反映了叶片的振动形状，从而更准确地结合SAFT图进行共振点的判断。

3.2 离心式压缩机共振规律探究

本次计算中，为探索压缩机叶轮共振的规律，为压缩机的共振预测提供参考，简化压缩机叶轮的逆向设计过程，计算了前8阶模态，并对于叶轮的固有频率以及模态阵型进行分析总结。

3.2.1 转速对叶轮模态的影响

本文计算了转速0～27 535 r/min中多个转速下的不同阶次、不同节径的固有频率，并分别求出同一阶次和同一节径下的最大值和最小值之间的差值百分比，结果见表2。

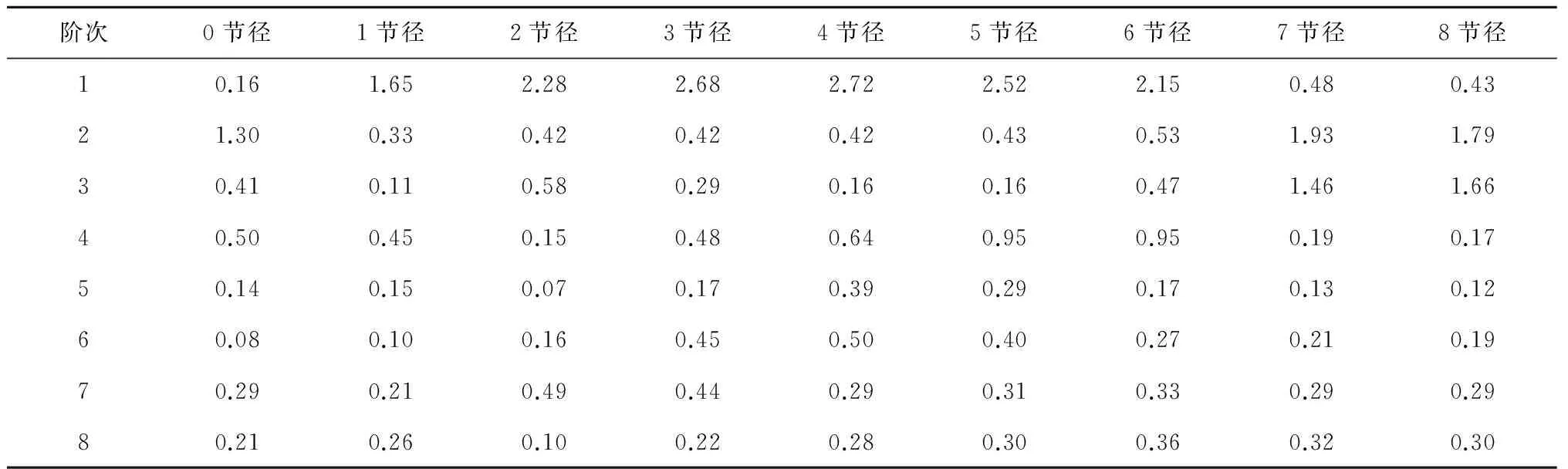
表2 固有频率最大、最小值之间的差值百分比 (%)

由表2中的数据可以得出，转速从0～27 535 r/min，固有频率变化幅度≤3%，大部分的固有频率的变化幅度≤1%，并且随着阶次变大，变化幅度呈现整体下降趋势，可以基本忽略转速对叶片固有频率的影响。

本文为寻找不同阶次以及不同节径之间固有频率之间的关系，并根据上文结论，取叶轮的固有频率为不同转速下的平均频率作为叶轮的标准的固有频率，为以下的计算打下基础。

3.2.2 阶次对叶轮模态的影响

提取前8阶的最大、最小频率，计算最大、最小值的变化率，结果见表3。

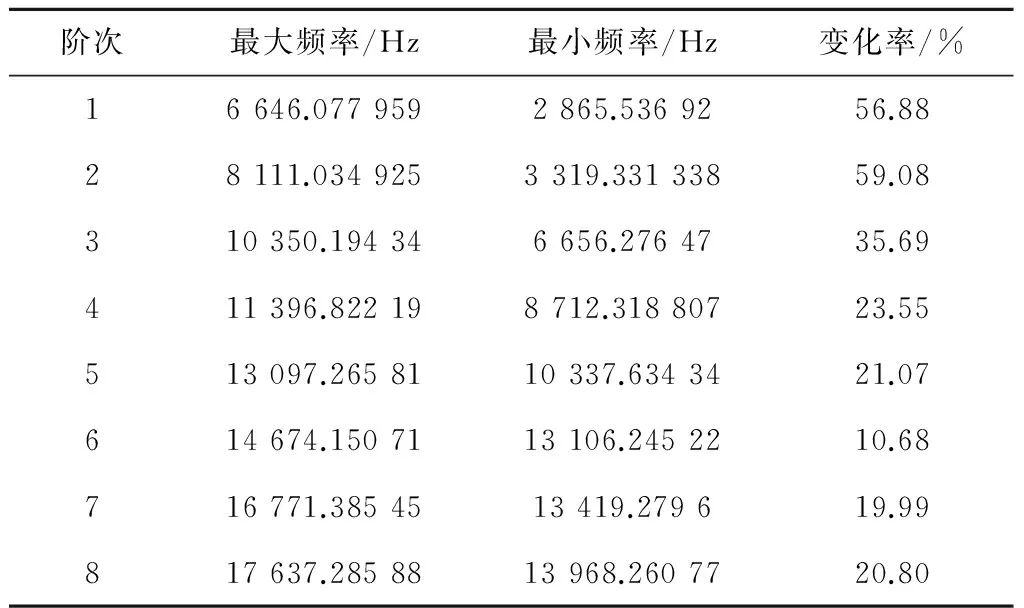
表3 阶次对叶轮模态的影响

将最大值和最小值按照阶次进行绘图，得到固有频率变化图如图10和图11所示。

图10 固有频率最大值变化规律

图11 固有频率最小值变化规律

根据图10和图11可得出如下结论：1)叶轮的固有频率基本随阶次呈现线性变化；2)叶轮同一阶次的固有频率最大值和最小值的变化率呈现下降趋势，因为固有频率总体是在增大的，即最大值和最小值的固有频率差值大小会维持在一个基本不变的水平。

通过上述试验数据，可以发现叶轮的共振固有频率有一定的规律可以探究，对于叶轮固有频率的预测以及压缩机叶轮的稳定性有较大的意义。

4 结语

本文基于美国某型号增压机的离心式叶轮，对叶轮进行了逆向设计，通过三坐标测量仪提取叶轮的几何数据，通过气动分析分析了叶轮的逆向可靠性。

为进一步确认叶轮的稳定性，本文采用了SAFT图法对叶轮进行了分析。结果表明，SAFT图法可以很好地应用在离心式叶轮的分析中，并且采用SAFT图法可以避免虚假共振点和评估共振裕度，为离心式叶轮的逆向设计提供了更好的保障。

为简化叶轮的稳定性分析，本文对离心式叶轮共振的规律进行了探究，得出了一系列初步结论，为叶轮的模态分析提供了一定的指导。

[1] 丁有宇，等. 汽轮机强度计算[M]. 北京：水利电力出版社, 1985.

[2] 王仲博, 张永宁, 袁平, 等. 660 mm叶片振动特性测试与分析[J]. 热力发电, 1994(6):36-40.

[3] 褚玉喜, 陆伟. 整圈自锁叶片(ILB)的设计及其动静频试验[J]. 热力透平, 2002(3):15-20.

[4] Singh M P, Vargo J J, Schiffer D M, et al. Safe diagram:a design and reliability tool for turbine blading[DB/OL]. [2004-03-13]. http://www.dresser-rand.com/e-tech/PDF% 20Files/tp024.pdf.

[5] 杨猛, 徐新喜, 白松, 等. 涡旋压缩机模态试验与有限元分析[J]. 噪声与振动控制, 2013, 33(6):15-17.

[6] 孔祥强, 陈丽娟, 郑瑞, 等. 制冷压缩机配管系统模态分析及振动特性[J]. 北京工业大学学报, 2016, 42(6):825-831.