薄膜天线结构模态参数的在轨辨识
吕娟霞, 蔡国平, 彭福军, 张 华, 吕亮亮
(1. 上海交通大学 工程力学系 海洋工程国家重点实验室,上海 200240; 2. 上海宇航系统工程研究所,上海 201109)
为了对航天柔性结构进行精确控制,必须准确获得其模态参数信息。传统的方法是对柔性结构进行有限元分析并结合地面试验,来获得其模态参数信息。但是由于地面空气阻力和重力的影响,地面试验难以模拟真实在轨状态,这会导致得到的参数与真实情况之间产生误差,尤其是对于大尺寸柔性结构误差将会变得很大。解决该问题的途径之一是进行模态参数的在轨辨识,通过柔性结构在太空中的真实响应数据采用一定的参数辨识技术来获得其真实模态参数。
大型柔性结构在航天领域得到了广泛应用,如薄膜天线、太阳帆板等,这一类结构具有低刚度、高柔性、弱阻尼以及形体庞大等特点,从而使得结构的固有频率低而且密集。例如美国喷气推进实验室研制的天线系统,前12阶模态频率范围为0~1.6 Hz,频率间隔最大为0.043 Hz,最小为0.005 Hz[1]。传统的频域法虽然可以直观地逐个识别模态,并能滤去大部分噪声,但计算时需要采样平均,花费时间长,而且对于低频密集模态辨识精度不高。时域辨识方法在处理手段以及估计密集模态方面都要优于频域方法。ERA(Eigensystem Realization Algorithm)[2-3]作为一种时域模态参数辨识方法,具有辨识精度高、抗噪能力强的优点,在国内外已经被广泛应用于大型柔性航天器固有频率的辨识。例如,美国NASA利用在轨数据对哈勃望远镜进行了在轨模态辨识[4];国际空间站上曾经开展了5次模态参数的在轨辨识试验[5];日本NASDA对ETS-VI进行了挠性参数的在轨辨识工作[6];俄罗斯的和平号空间站总共进行了1年时间的在轨模态试验[7]。然而需要指出的是,目前关于航天器挠性参数辨识技术的研究中,固有频率辨识的研究居多,少有关于模态辨识的研究报道。
本文对航天柔性结构固有频率和模态的在轨辨识技术进行研究。采用Abaqus软件计算得到系统的动力学响应数据,采用ERA方法辨识结构的固有频率和模态,最后以柔性悬臂梁和薄膜天线结构为对象进行数值仿真验证。
1 薄膜天线结构描述
薄膜天线结构如图1所示,结构主要由薄膜阵面、豆荚杆、端杆、张力撑杆、张拉机构、搭接结构等构成。豆荚杆为柔性杆,它与端杆固连成为薄膜结构的支撑框架。端杆刚度远大于豆荚杆刚度,可作刚性部件处理。豆荚杆在薄膜机构展开状态满足一定的刚度、屈曲载荷要求,它是由两个横截面呈“Ω”形状的薄壁壳体所构成,它们的半圆形凹面相对。豆荚杆收拢时首先压平两薄壁壳体,展开时则依靠自身弹性应变能从扁平状态恢复为管状。薄膜阵面是结构的核心部件,展开后边缘为抛物线形,横向11跨,纵向3跨。阵面为柔性材料,抗弯刚度小,不能受压。阵面纵向共4个张拉点,角向共4个张拉点,通过拉索直接与两侧端杆连接。阵面横向共20个张拉点,每个张拉点通过拉索与张拉机构连接;张拉机构带动拉索收缩实现膜面张紧,使膜面本身具有预应力;通过调节张拉机构可以改变膜面预应力水平,从而改变膜面刚度。张拉机构另一侧与张力撑杆固结。张力撑杆刚度很大,计算时作刚性部件处理,共9根,浮动在阵面一侧,与端杆平行。膜面张紧后,张力撑杆承受张拉机构的反作用力,确保预应力不传递至豆荚杆。张力撑杆通过搭接装置与豆荚杆连接,张力撑杆与搭接装置固结,且只能沿豆荚杆轴向自由移动。薄膜天线详细的物理参数等可以参见文献[8-10]。
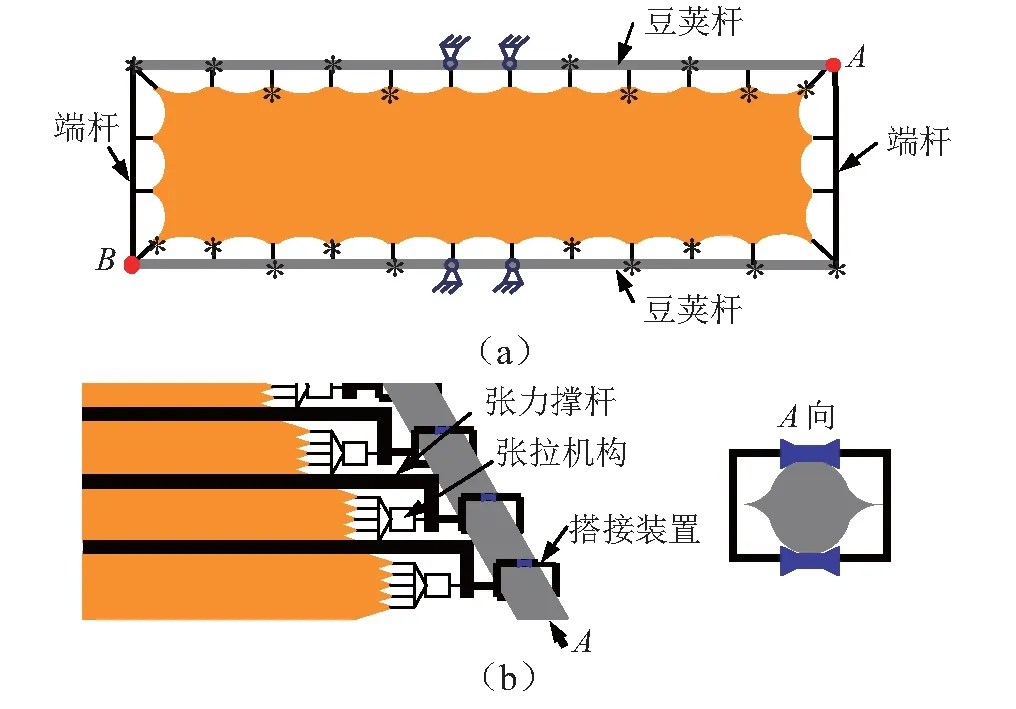
图1 薄膜天线结构Fig.1 The structure of the membrane antenna
2 基于ERA的系统参数辨识
特征系统实现算法(ERA)是一种发展成熟的时域模态参数识别算法,它利用系统的脉冲响应数据构造Hankel分块矩阵,并对其进行奇异值分解,从而求得系统的低维模型实现。文献[11-12]中分别给出了基于系统状态和基于加速度的ERA的计算格式,本文采用基于系统状态的ERA方法进行模态参数辨识,基本思想简述如下。
系统的连续状态方程可表示为
(1)
式中:x∈R2n×1为系统状态向量;A1∈R2n×2n为系统矩阵;B1∈R2n×d为控制矩阵;d为输入通道数;y(t)∈Rq×1为输出向量;q为输出通道数;u(t)∈Rd×1为输入向量;C1∈Rq×2n为观测矩阵;D1∈Rq×d为直接影响矩阵。当输出向量全部为位移时,C1=[Iq×n0q×n]; 当输出向量全部为速度时,C1=[0q×nIq×n]。
设数据采样周期为Δt, 连续系统可以离散为如下差分状态方程形式
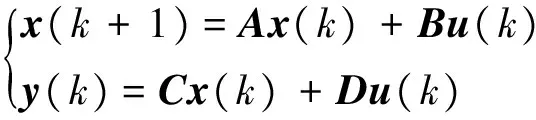
(2)
其中,
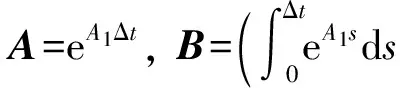
(3)
构造如下(s+1)×(l+1)块Hankel分块矩阵
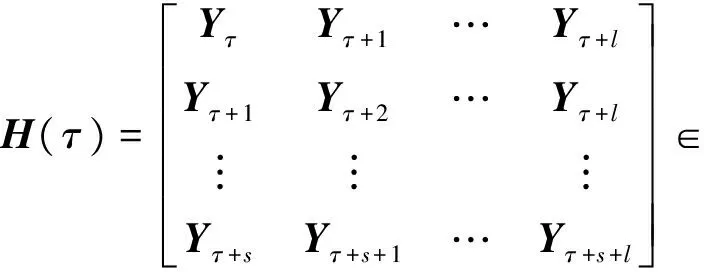
(4)
式中:Y=[y(0)y(1)y(2) …y(d-1)]为由系统输出向量构成的q×d维矩阵。
将H(τ)写成如下形式
(5)
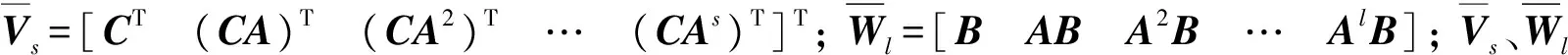
H(0)=UNVT
(6)
式中:U、V为酉阵;N为奇异值对角阵,N=diag(d1,d2,…,dr,dr+1,…),d1≥d2≥…≥dr≥dr+1≥…≥0。 对H(0)进行奇异值分解以后, 需要一个ε来判断奇异值的取舍, 若r满足如下条件
(7)
即dr之后的特征值远小于前r个特征值, 则取r作为系统的阶次。
取Ur为U的前r列,Vr为V的前r列,Nr=diag(d1,d2,…dr)。 定义如下矩阵
(8)
系统的最小实现(Ar,Br,Cr,Dr)可以确定为
(9)
式中:Dr的辨识详见文献[11-12]。
设矩阵Ar的特征值矩阵为Z, 特征向量矩阵为ψ, 则有
ψ-1Arψ=Z,Z=diag(z1,z2,…,zr)
(10)
将式(10)代入式(3), 并结合指数矩阵的性质可知Ar的特征向量仍为A1的特征向量, 且A1的特征值λi可表示为
(11)
由振动理论,得到
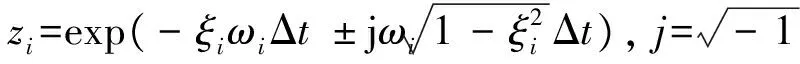
(12)
式中:ωi和ξi分别为动力学系统的无阻尼固有频率和阻尼比。从而可以得到系统的无阻尼固有频率为
(13)
由观测方程y=C1x+D1u可知系统的包含r阶振型的模态矩阵(振型矩阵)φ可表示为
φ=Crψ
(14)
3 数值仿真
本节进行数值仿真,验证ERA方法的有效性。首
先以一个柔性悬臂梁为对象开展固有频率和模态的辨识仿真,然后以一个薄膜天线结构为对象进一步进行仿真验证。
3.1 柔性梁模态参数辨识
柔性梁长为20 m,横截面为0.01 m×0.01 m的矩形,材料密度为350 kg/m3,材料弹性模量为6×109Pa。在梁自由端施加10 N·s的脉冲激励,通过梁上均布的25个传感器采集梁的响应,采样频率为1 000 Hz,采集1~4 s内的响应数据。表1中结果分别为采用Abaqus、FFT和ERA方法所得到的梁的前5阶固有频率。可以看出,ERA方法辨识得到的梁的前5阶固有频率与Abaqus的计算结果接近。由于第1阶频率过低,FFT并没有辨识得到梁的第1阶频率,辨识得到的其余4阶频率与Abaqus的计算结果接近。图2所示为采用ERA方法辨识所得到的梁的前4阶模态,可以看出,辨识所得模态也接近Abaqus软件的结果;虽然高阶模态结果存在误差,这可以通过增加传感器数量得以消除。
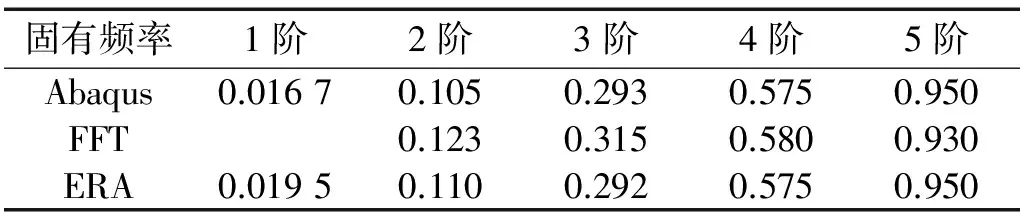
表1 悬臂梁固有频率辨识结果

图2 悬臂梁前4阶振型Fig.2 The first four modal shapes of the cantilever beam
3.2 薄膜天线结构模态参数辨识
首先考虑薄膜天线结构固有频率的辨识。如图1所示,将薄膜天线结构的中间4点铰接,基于Abaqus仿真计算平台计算薄膜结构的固有频率,在A点施加微小扰动,采用Abaqus软件计算薄膜结构的动力学响应和固有频率。辨识时取数据采样频率为1 000 Hz,采样时间段为1~8 s,在膜面和框架上选择图1所示(星号标记处)共20个点的位移数据用于辨识。表2所示为采用ERA方法辨识所得到的结果,可以看出,薄膜天线结构前5阶固有频率均小于0.5 Hz,为低频密集结构,辨识结果与Abaqus软件结果吻合良好。值得指出的是,因为薄膜天线结果为低频密频结构,FFT方法将无法有效辨识出结构的固有频率。
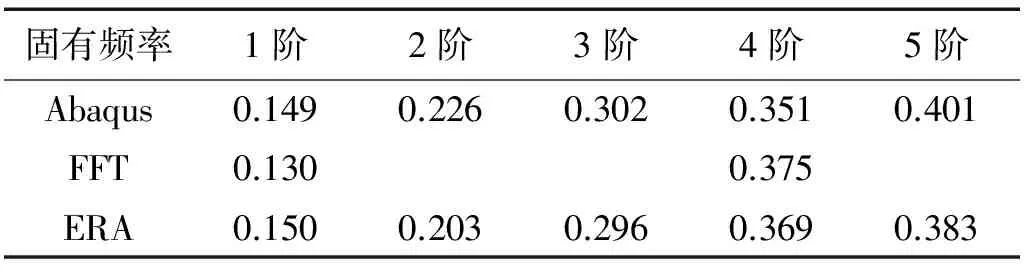
表2 薄膜天线结构固有频率辨识结果
然后考虑薄膜天线结构模态的辨识。在图1所示结构的A、B两点施加微小扰动,采用Abaqus计算结构的动力学响应。先考虑1阶模态的辨识,采样频率1 000 Hz,采样时间段为1~4 s,采集图3(a)所示膜面和框架上共44个点的位移数据用于辨识。图4(a)为辨识的结果,可以看出,1阶模态中豆荚杆和膜面都为横向弯曲振动,辨识结果与Abaqus的结果基本一致。对于薄膜天线结构的2阶模态,其复杂性远高于1阶模态,豆荚杆和膜面振动形式不同,为有效辨识出2阶模态,需要增加传感器的测点数量。本文采用80个测点,如图3(b)所示,数据采样频率取为1 000 Hz,采样时间段选择为2~5 s。图4(b)为2节模态的辨识结果,可以看出,增加测点数量后2阶模态也能得到有效辨识。在此需要说明的是,随着需要辨识模态阶次的增加,利用ERA方法仍可辨识得到豆荚杆的模态,但是膜面的振动情况将变得愈加复杂,必须增加膜面上采样点的个数方可得到有效辨识。

图3 薄膜天线结构采样点示意图Fig.3 Sketch map of sampling points on the membrane antenna
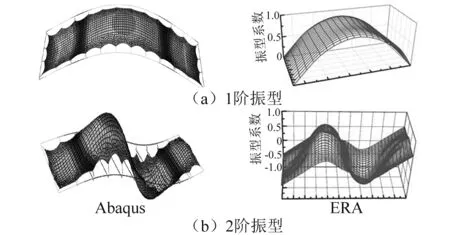
图4 薄膜天线结构1、2阶振型Fig.4 The first two modal shapes of the membrane antenna
4 结 论
本文对柔性结构固有频率和模态的在轨辨识技术进行了研究。并且以柔性梁和薄膜天线结构为对象进行了数值仿真验证。研究结果显示,当结构的固有频率足够分开时,ERA方法可以有效地辨识出结构的固有频率和模态,测点数量越多模态辨识精确越高;当结
构为低阶频率密集时,ERA方法可用于低阶固有频率和模态的辨识。
[ 1 ] 赵发刚, 周徐斌, 申军烽, 等. 航天器在轨模态辨识技术的探讨[C]//国际功能制造与机械动力学会议. 杭州: 国际功能制造与机械动力学会议论文集, 2011.
[ 2 ] JUANG J N, PHAN M. Identification and control of mechanical systems [M]. New York: Cambridge University Press, 2001.
[ 3 ] JUANG J N, PAPPA R S. An eigensystem realization algorithm for modal parameter identification and modal reduction [J]. Journal of Guidance, Control and Dynamics, 1985, 8(5): 620-627.
[ 4 ] ANTHONY T, ANDERSEN G. On-orbit modal identification of the Hubble space telescope [C]//Proceedings of the American Control Conference. Seattle: IEEE, 1995.
[ 5 ] KAOUK M, MCNEILL S, HALEY S, et al. Shuttle-ISS flight-7A on orbit test verification: pre and post flight analysis [C]//22nd International Modal Analysis Conference.Dearborn:Society for Experimental Mechanics, 2003.
[ 6 ] ADACHI S, YAMAGUCHI I, KIDA T, et al. On-orbit system identification experiments on engineering test satellite-VI [J]. Control Engineering Practice, 1999, 7(7): 831-841.
[ 7 ] KIM H M, KAOUK M. Mir structural dynamics experiment: first test and model refinement [C]//Proceedings of the 40th Sustainable Design and Manufacturing Conference. St. Louis: AIAA, 1999.
[ 8 ] 姬鸣. 薄膜天线支撑杆展开机构的研制[D]. 哈尔滨:哈尔滨工业大学, 2011.
[ 9 ] 邹涛. 薄壁管状空间伸展臂收展数值模拟与试验[D]. 上海:上海交通大学, 2013.
[10] 胡宇. 空间薄膜阵面预应力及结构特性分析[D]. 上海:上海交通大学, 2012.
[11] 刘松, 蔡国平, 董兴建. 海洋平台的时域低维建模与主动控制研究[J]. 力学学报, 2011, 43(4): 737-745.
LIU Song, CAI Guoping, DONG Xingjian. Time-domain dynamic modeling and active control of offshore platform [J]. Chinese Journal of Theoretical and Applied Mechanics, 2011, 43(4): 737-745.
[12] 谢永, 刘盼, 蔡国平. 基于加速度信号的柔性板的挠性参数辨识[J]. 力学学报, 2014, 46(1): 128-135.
XIE Yong, LIU Pan, CAI Guoping. Parameter identification of flexible plate based on the acceleration output [J]. Chinese Journal of Theoretical and Applied Mechanics, 2014, 46(1): 128-135.

