基于Donnell-Mushtari理论的弹性基础薄壁圆柱壳的稳态响应研究
杨永宝, 危银涛, 李雪冰, 张新月
(1.清华大学 汽车安全与节能国家重点实验室,北京 100084; 2. 燕山大学 车辆与能源学院,秦皇岛 066004)
薄壁圆柱壳作为一种简单、高效的结构在各工程领域均得到广泛应用,如常见的轮胎、油罐、飞机、潜艇等具体部件。但类似结构在受到外界复杂激励作用后易出现失稳等现象而影响正常工作,故薄壁圆柱壳动力学特性的研究对此类结构的设计和分析有重要工程意义。
有关文献十分丰富,尤其是针对简支、固支等经典边界条件下圆柱壳固有振动特性的研究[1-8]。Leissa[9]在著名的壳振动理论一书中对数量众多的文献进行了综述,系统总结了常见壳理论及不同类型壳的自由振动问题。许多学者基于不同壳理论对经典边界条件下圆柱壳的振动响应进行了针对性研究。Sheng等[10-11]分别基于Donnell理论与Novozhilov壳体理论对简支条件下的各向同性圆柱壳响应问题进行研究。Christoforou等[12]针对简支条件下的正交各向异性圆柱壳受到径向冲击后的响应问题展开研究。Jafari等[13]基于love壳理论对复合材料圆柱壳的自由和强迫振动响应展开研究,边界条件为固支-自由边界。马旭等[14]在波传播分析方法基础上,采用改进傅里叶级数的方法给出了两端弹性基础上的圆柱壳在任意径向点力激励下的振动响应,实质是用梁弯曲振动模态振型来近似柱壳轴向振型以实现圆柱壳振动在周向与轴向的解耦,在某些情况下误差较大。还有许多类似研究[15-18],但主要是简支等经典边界条件下圆柱壳的稳态响应研究,而针对两端弹性边界条件下薄壁圆柱壳(以下简称弹性基础圆柱壳)稳态响应的求解研究尚比较欠缺,有关研究还存在误差较大等问题。
本文针对弹性基础上有径向预压力作用的圆柱壳展开研究。基于经典的Donnell-Mushtari柱壳理论,对圆柱壳的固有振动特性进行分析,求得谐波激励作用下的强迫振动稳态响应,并针对所取基础模态数量及阻尼系数大小对于薄壁圆柱壳稳态响应的影响进行了讨论研究。
1 固有振动特性
薄壁圆柱壳模型如图1所示,建立柱坐标系(x,θ,r),x,θ,r分别为其轴向、周向和径向的坐标轴,u,v,w分别为柱壳中面上任一点的轴向、周向和径向位移,圆柱壳的长度为L,平均半径为R,厚度为h。在圆柱壳的两端均布相应的轴向、周向、径向和扭转方向的弹簧,刚度分别为ku,kv,kw,kφ。
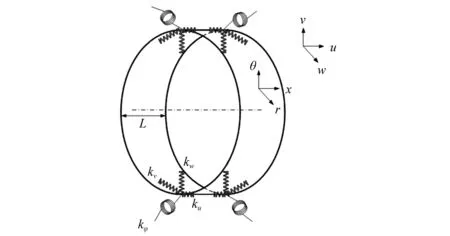
图1 圆柱壳及相应的坐标系示意图Fig.1 Cylindrical shell and coordinate systems
柱壳自由振动控制方程为
(1)
式中:L(u,v,w)为相应的微分算子。
基于经典的Donnell-Mushtari柱壳理论,考虑在圆柱壳内壁上沿径向均匀分布的初始内压力P0,得到自由振动微分方程为
(2)
(3)
(4)
其中,
(5)
假设圆柱壳的位移表达式为
(6)
将上述位移表达式(6)代入振动微分方程式(2)~式(4)中,可得表达式
(7)
若式(7)有非零解,则左侧矩阵行列式结果为零。整理可得到关于λ的8次特征方程为
λ8+g3λ6+g2λ4+g1λ2+g0=0
(8)
其中,
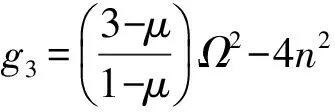
(9)
(10)
式中:n为周向波数;ω为圆频率;Ω为无量纲频率参数。
特征方程式(8)是一个与轴向波数有关的无量纲参数λ的8次方程,有正负两组共8个解λi(i=1, 2, …, 8),解的可能形式有实数、虚数和复数三种,λi为纯实数时代表轴向的传播波,λi为纯虚数时为轴向的近场波,λi为复数时代表沿轴向衰减的传播波[19]。特征方程式(8),随着参数的变化,会出现不同类型的根值,理论上共有九种不同组合形式的根值,而不应简单的直接假设为某些特定类型,如一对纯实根、一对纯虚根和两对复根,否则可能会出现漏解问题。本文充分考虑了这一点,避免了类似问题产生,同时得到精确解。
基于特征方程式(8)得到根值表达式,代入方程式(7),求得振幅比系数ηi和εi
(11)
进而将3个方向的位移表达式写出
(12)
对不同的边界条件,薄壁圆柱壳的位移和内力等将对应满足不同的条件。
对两端弹簧支撑边界条件下的薄壁圆柱壳,当x=-L/2时,满足

(13)
当x=L/2时,满足
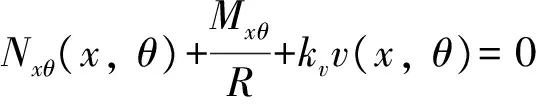
(14)
式(13)和式(14)中,
(15)
将式(12)代入式(13)和式(14)中,整理之后得到关于C1~C8的八元齐次代数方程组,若方程组存在相应的非零解,则系数行列式结果为0,可求得薄壁圆柱壳的固有频率及对应的模态振型。
求解过程没有进行做任何近似,因此计算所得结果是基于Donnell-Mushtari理论所得到的最精确计算结果。
2 稳态响应
为简化相应表达式和计算过程,求解稳态响应时,不考虑圆柱壳内部压力的影响。
在外载荷激励作用下,薄壁圆柱壳满足下列动力学方程
(16)
上述动力学方程的解可设为
(17)
将以上解代入外载荷作用下的动力学方程中,可得
(18)

(19)
因此,整理式(18)、式(19)后可得到
(20)
(21)
其中,对应广义力Fmn(t)为
(22)
对应的广义质量Mmn为
(23)
利用二阶微分方程式(21),求解得到每阶模态所对应的Tmn(t)值,然后将结果代入式(17),即可求得相应的强迫振动稳态响应结果。

若作用在u、v方向的激励力为0,w方向的激励力fw为
fw=f0eiωtδ(θ-θ*)δ(x-x*)
(24)
则,对应的广义力为
(25)
有关Tmn(t)的二阶微分方程则变为(m,n指相对应的模态阶次)
(26)
将每阶模态所对应的广义力和广义质量等代入式(26),求得各阶模态所对应的Tmn(t),并将所得结果代回式(17)中,求得强迫振动响应。
基于式(26)可求得Tmn(t)
(27)
若激励力为正弦波信号f0sin(ωt),初始条件为0,则模态坐标通解取式(27)的虚部,为
(28)
(29)
3 算例分析
3.1 与文献中结果的对比
为验证本文理论计算方法的准确性,本节针对两个经典算例,将本文计算方法所得结果与有关文献中的数据进行对照,如表1和表2所示。其中,Karczub中的计算结果基于Flügge经典薄壳理论得到,文献[20]采用的是有限元分析方法,Li采用了波传播方法。
表2给出了通过本文计算方法得到的固有频率结果及有关文献中的数据,对比结果显示,本文方法的计算误差较小,结果准确。
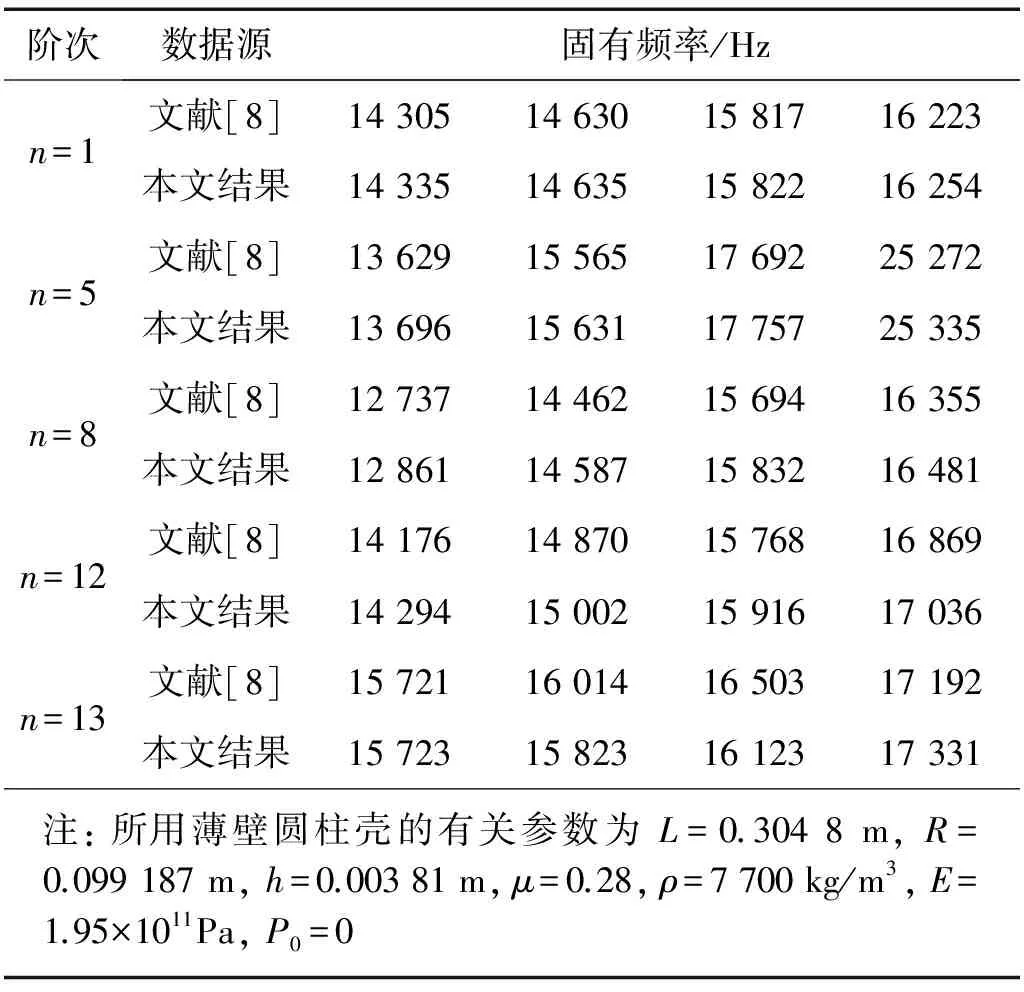
表1 简支但有轴向位移约束的边界条件下, 基于本方法所得结果与有关文献所得结果的对比
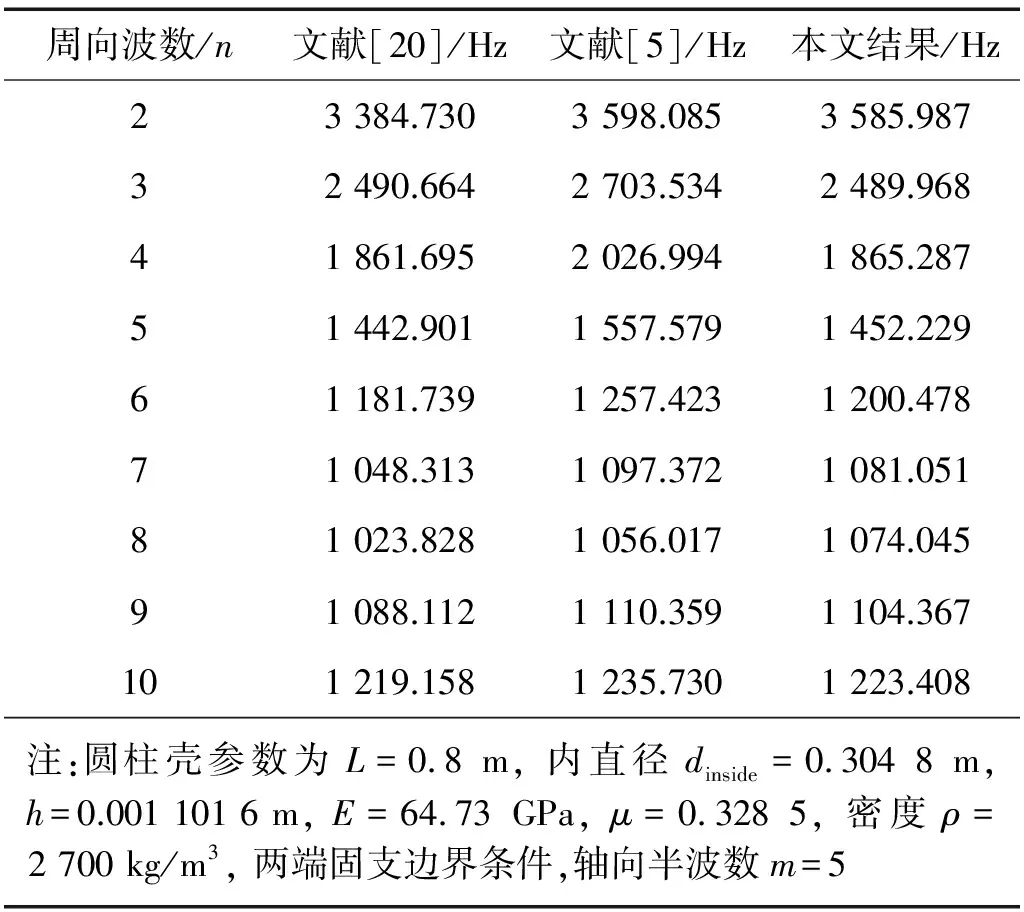
表2 固有频率的理论计算结果与文献中结果对照
3.2 参数分析
为分析不同周向波数和轴向半波数与圆柱壳固有频率的关系,分别采用有限元方法和本文方法进行算例分析,模型参数为:R=0.5 m,h=0.01 m,L=4 m,E=1.5×1011Pa,μ=0.3,ρ=7 000 kg/m3,圆柱壳两端的径向均布弹簧的刚度kw=1 000 N/m, 内压力P0=0。 其余弹簧刚度为0,得到结果如图2所示。

图2 波数与薄壁圆柱壳固有频率间的关系Fig.2 Correlation between wave number and free vibration frequency of thin-walled cylindrical shell
从图2可得以下几点结论:本文计算得到的薄壁圆柱壳固有频率与有限元方法计算得到的结果比较一致;随着轴向半波数的增加,圆柱壳的固有频率总体呈增大趋势;而在不同的轴向半波数下,周向波数与固有频率间的关系总体上也是一致的,随n值的增加先降低而后升高,且变化趋势随轴向半波数的变化而略有不同。
4 稳态响应的计算和讨论
基于本文方法可对任意边界条件的下的薄壁圆柱壳进行自由振动频率和稳态响应的计算,本文以径向简单支撑弹簧边界条件为例进行计算和讨论。有关参数同4.2节的算例。
4.1 谐波激励下的柱壳稳态响应
设外力作用在薄壁圆柱壳的(L/2,0)位置处,激励为fsin(ωt),f=1 N。
利用本文方法,首先基于圆柱壳的有关参数计算得到前25阶固有频率及对应模态振型,之后基于模态数据进行叠加计算,得到稳态响应幅频曲线,如图3所示。

图3 圆柱壳稳态响应幅频曲线Fig.3 Amplitude-frequency response curve of cylindrical shell
从图3可看出,在最低阶次模态所对应的58.76 Hz频率处,出现了最大的径向位移响应。而后,随着频率的增加,径向位移响应总体上呈降低趋势。某些阶次模态所对应的径向位移较小,因此未在幅频曲线中显著体现。
4.2 所用模态数量的影响
计算圆薄壁圆柱壳的稳态响应时,模态截断数量对于稳态响应的计算会产生影响。为分析这种影响,分别使用前6阶、12阶及25阶模态来计算薄壁圆柱壳在谐波激励下的径向位移稳态响应,得到如图4~图6所示结果。
观察图4~图6圆柱壳稳态径向位移响图不难发现,对于前几阶振动模态,选择使用前6阶模态、12阶模态及25阶基础模态叠加计算所得径向响应位移值的变化幅度很小。即对于两端弹簧支撑条件下受到径向谐波激励时的薄壁圆柱壳的稳态位移响应求解问题,采用数量较少的基础模态也可满足基本精度要求。对本文算例,只需要前6阶基础模态数据即可实现很小的计算误差,以图6结果为基准,计算得到的第一阶模态所对应的径向位移误差仅为0.37%。
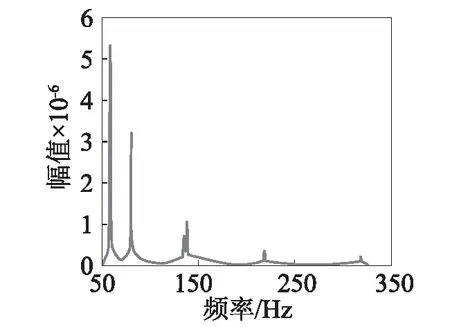
图4 基于前6阶模态叠加计算得到的稳态响应幅频曲线Fig.4 Amplitude-frequency curve of steady-state response based on the superposition of first six modes
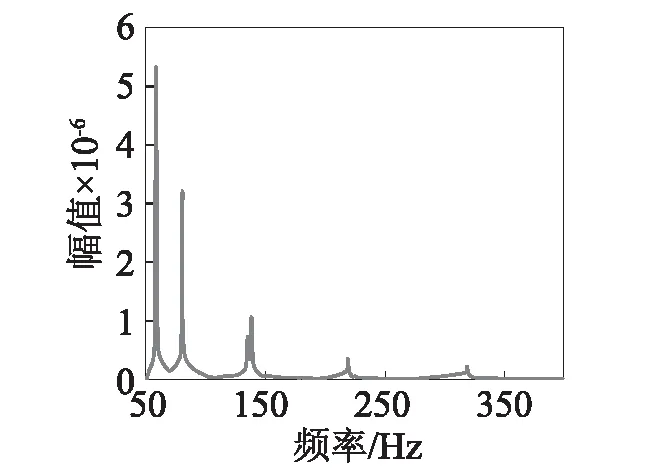
图5 基于前12阶模态叠加计算得到的稳态响应幅频曲线Fig.5 Amplitude-frequency curve of steady-state response based on the superposition of first twelve modes

图6 基于前25阶模态叠加计算得到的稳态响应幅频曲线Fig.6 Amplitude-frequency curve of steady-state response based on the superposition of first twenty-five modes
4.3 阻尼系数的影响
在计算圆柱壳的位移稳态响应时,须计入阻尼的影响,为分析阻尼系数对于圆柱壳位移稳态响应的影响,基于计算得到的前25阶模态数据,分别求解阻尼因子为0.005、0.010、0.015条件下的圆柱壳的径向位移响应,得到如图7所示的幅频特性曲线。
从图7不难看出,阻尼对薄壁圆柱壳的稳态位移响应影响显著,随着阻尼因子的增加,圆柱壳的径向位移响应出现显著的减小。在较高频段,幅频曲线变得平滑,没有了明显峰值。

图7 三种不同阻尼因子条件下的薄壁圆柱壳径向位移幅频响应Fig.7 Amplitude-frequency curve of radial displacements of thin-walled cylindrical shell for three different damping factors
6 结 论
本文基于经典的Donnell-Mushtari圆柱壳振动理论,得到了考虑初始内压力的弹性基础上薄壁圆柱壳的固有频率及强迫振动稳态响应的计算公式。主要结论可归纳如下:
(1)本文方法计算所得结果与有关文献中的数据结果相比较,误差较小,精度较高。
(2)基于本文算例,较少数量的模态叠加即可实现较为精确的稳态响应计算。即选择适当数量的基础模态用于薄壁圆柱壳稳态响应叠加计算,可在保证精度的情况下提高计算效率。
(3)基于本文算例,阻尼因子对于薄壁圆柱壳稳态响应的影响较大,当阻尼因子增大时,柱壳的稳态响应将显著减小,稳态响应幅频曲线的部分峰值变得不明显。
(4)本文方法不仅可针对一般的弹性基础边界条件下的薄壁圆柱壳的自由振动及谐波激励稳态响应进行求解,还可用于解决其他各种边界条件下的薄壁圆柱壳的振动特性问题。
[ 1 ] SAITO T, ENDO M. Vibration of finite length, rotating cylindrical shells[J]. Journal of Sound and Vibration, 1986, 107(1): 17-28.
[ 2 ] SMITH B L, VRONAY D F. Free vibration of circular cylindrical shells of finite length[J]. AIAA Journal, 1970, 8(3): 601-603.
[ 3 ] ZHANG X M, LIU G R, LAM K Y. Vibration analysis of thin cylindrical shells using wave propagation approach[J]. Journal of Sound and Vibration, 2001, 239(3): 397-403.
[ 4 ] IP K H, CHAN W K, TSE P C, et al. Vibration analysis of orthotropic thin cylindrical shells with free ends by the rayleigh-ritz method[J]. Journal of Sound and Vibration, 1996, 195(1): 117-135.
[ 5 ] LI Xuebin. Study on free vibration analysis of circular cylindrical shells using wave propagation[J]. Journal of Sound and Vibration, 2008, 311(3): 667-682.
[ 6 ] DYM C L. Some new results for the vibrations ofcircular cylinders[J]. Journal of Sound and Vibration, 1973, 29(2): 189-205.
[ 7 ] SOEDEL W. Simplified equations and solutions for the vibration of orthotropic cylindrical shells[J]. Journal of Sound and Vibration, 1983, 87(4): 555-566.
[ 8 ] KARCZUB D G. Expressions for direct evaluation of wave number in cylindrical shell vibration studies using the Flügge equations of motion [J]. The Journal of the Acoustical Society of America, 2006, 119(6): 3553-3557.
[ 9 ] LEISSA A W. Vibration of shells[M]. New York: Acoustical Society of America, 1993.
[10] SHENG J. The response of a thin cylindrical shell to transient surface loading [J]. AIAA Journal, 1965, 3(4): 701-709.
[11] WARBURTON G B. Harmonic response of cylindrical shells [J]. Journal of Engineering for Industry, 1974, 96(3):
994-999.
[12] CHRISTOFOROU A P, SWANSON S R. Analysis of simply-supported orthotropic cylindrical shells subject to lateral impact loads [J]. Journal of Applied Mechanics, 1990, 57(2): 376-382.
[13] JAFARI A A, KHALILI S M R, AZARAFZA R. Transient dynamic response of composite circular cylindrical shells under radial impulse load and axial compressive loads [J]. Thin-Walled Structures, 2005, 43(11): 1763-1786.
[14] 马旭, 杜敬涛, 杨铁军, 等. 基于波传播方法的边界条件对圆柱壳振动特性的影响分析[J]. 振动工程学报, 2009, 22(6): 608-613.
MA Xu, DU Jingtao, YANG Tiejun, et al. Analysis of influence of boundary conditions on cylindrical shell dynamics based on wave propagation approach [J]. Journal of Vibration Engineering, 2009, 22(6): 608-613.
[15] 王宇, 罗忠. 薄壁圆柱壳构件受迫振动的响应特征研究[J]. 振动与冲击, 2015, 34(7): 103-108.
WANG Yu, LUO Zhong. Forced vibration response characteristics of thin cylindrical shell [J]. Journal of Vibration and Shock, 2015, 34(7): 103-108.
[16] 罗忠, 王宇, 孙宁, 等. 不同边界条件下旋转薄壁短圆柱壳的强迫振动响应计算[J]. 机械工程学报, 2015, 51(9): 64-72.
LUO Zhong, WANG Yu, SUN Ning, et al. Forced vibration response calculation of rotating short thin cylindrical shells for various boundary conditions [J]. Journal of Mechanical Engineering, 2015, 51(9): 64-72.
[17] 李学斌. 圆柱壳稳态动力响应分析[J]. 舰船科学技术, 2000 (6): 1-5.
LI Xuebin. Steady-state dynamic response analysis of cylindrical shell[J]. Ship Science and Technology, 200(6): 1-5.
[18] 左言言, 宫镇. 圆柱壳受激振动的分析研究[J]. 农业机械学报, 1998, 29(1): 88-93.
ZUO Yanyan, GONG Zhen. Study on the excited vibration of a cylindrical shell[J]. Transactions of the Chinese Society for Agricultural Machinery, 1998, 29(1): 88-93.
[19] 陈正翔, 江松青. 圆柱壳中结构振动波的传播特性[J]. 振动工程学报, 1998, 11(4): 450-456.
CHEN Zhengxiang, JIANG Songqing. Dispersion characteristics of structure vibration waves in cylindrical shells [J]. Journal of Vibration Engineering, 1998, 11(4): 450-456.
[20] SANTIAGO J M, WISNIEWSKI H L. Convergence of finite element frequency prediction for a thin walled cylinder [J]. Computers and Structures, 1989, 32(3/4): 745-759.

