基于EDEM的轻型凿式深松铲土壤耕作载荷仿真分析

顿国强,陈海涛，李兴东，纪文义，朱 海，宋文龙

(1.东北林业大学 机电工程学院，哈尔滨 150040；2.东北农业大学 工程学院，哈尔滨 150030)

0 引言

保护性耕作技术通过采用深松、少耕及免耕播种技术代替传统的耕翻式整地技术，可有效提高土壤的蓄水保墒、抗旱、抗水蚀风蚀能力，以及土壤的有机质含量，培肥地力[1-2]。深松铲作为保护性耕作机具深松机的关键部件，其性能优良与否直接影响土壤的深松效果。国内外学者通常采用仿生设计、有限元仿真及试验研究等方法[3-8]，对深松铲进行设计研究：如白景峰、李博及吕秀婷等设计了狗獾爪趾式仿生深松铲，并进行了试验研究；张强与贾洪雷等利用有限元法对仿生钩形深松铲耕作阻力进行分析研究及试验验证；王景立及刘选伟等利用ANSYS Workbench进行了弧形深松铲模态分析研究；王宏立及张伟利用Pro/E和ANSYS对深松铲进行有限元静力学分析；齐关宇、刘林及赵艳忠等采用试验的方法研究了入土深度及铲形对深松铲耕作阻力的影响；李博及刘凡一等虽利用离散元法进行了深松铲耕作阻力的仿真分析研究，但并不深入。

本研究采用EDEM建立凿式深松铲的离散元仿真模型，并对其载荷进行空间分解，确定载荷的主要组成。同时，采用仿真试验的方法分析作业参数对深松铲耕作阻力及载荷波动状况的影响。

1 深松铲土壤深松仿真

1.1 颗粒接触模型

为描述深松铲土壤深松过程中土壤颗粒间及土壤颗粒与接触部件间的瞬态力学行为，EDEM系统默认多种接触力学模型[9-10]，以模拟不同的颗粒接触力学特性。本研究采用EDEM2.4版本系统默认的Hertz-Mindlin (no slip)接触力学模型[11-12]，此接触模型的法向及切向力由Hertz接触理论及Mindlin模型确定，且载荷包括由阻尼系数及恢复系数确定的阻尼分量，切向摩擦力库仑摩擦定律确定。此模型具有较高的计算精度，颗粒单元(Hertz-Mindlin)接触力学模型如图1所示。

图1 颗粒接触力学模型Fig.1 Model of particle contact forces

(1)

(2)

颗粒接触切向力及切向阻尼力由切向交叠量及切向刚度确定，其接触法向力表达式为

F法=-2·δ法·S法

(3)

(4)

1.2 深松铲土壤深松过程仿真

参考农业机械设计手册[13]，按适用30cm深松铲标准GB/T9788-1999，利用SolidWorks2009建立轻型凿式深松铲的三维实体模型(见图2)，并将深松铲模型另存为.igs格式文件。

图2 深松铲三维实体模型Fig.2 Deep shovel 3D model

利用EDEM 2.6建立凿式深松铲的离散元元仿真算例，选用Hertz-mindlin(no-slip)模型定义土壤颗粒之间、土壤颗粒与深松铲及土槽之间的颗粒接触力，查阅相关文献[14-18]，确定模型仿真参数设置如表1所示。

表1 模型仿真参数设置Table 1 Parameters setting of model simulation

为真实模拟深松铲的土壤深松过程，在保证运算结果正确的基础上，尽量降低计算机的运算量，土壤颗粒采用球体建模，颗粒半径5mm；软件自动计算土壤颗粒的质量属性[19]，并将上述建立的深松铲实体模型导入EDEM仿真算例模型，设定深松铲的作业速度为1m/s，方向为x轴负向，z轴负向为重力加速度方向。同时建立颗粒工厂及土槽实体模型，土壤颗粒数量40 000，生成速度z轴负向5m/s，生成速率100 000个/s，仿真步长5.831 9×10-5s，记录数据时间间隔0.000 5s，则深松铲的土壤深松离散元仿真模型如图3所示。

图3 深松铲离散元仿真模型Fig.3 Chisel-type deep shovel discrete element simulation model

如图4所示，利用EDEM 2.6后处理模块提取凿式深松铲的土壤深松过程的土壤绝对耕作阻力及其各轴方向分量数据。

图4 深松铲土壤耕作阻力Fig.4 Chisel-type deep shovel soil cutting force

由图4可知：凿式深松铲的土壤耕作阻力随着时间的推移，由0开始逐渐增大。其中，绝对土壤耕作阻力与其x轴分量具有相同的变化趋势，两力值的变化范围为150～375N之间；z轴分量为负值，即土壤对深松铲的竖直方向阻力向下，深松铲有自行入土的功能，且其力值在-240～-110N范围内变动；y轴分量数据在±50N范围内波动；且所有载荷数据在0.7s后趋于稳定；由上述分析可知：深松铲土壤耕作阻力主要由前进分量及竖直分量决定。深松铲的土壤耕作阻力统计数据如表2所示。

表2 载荷数据统计Table 2 Statistic of loading data N

2 作业参数对耕作阻力的影响

2.1 入土深度的影响

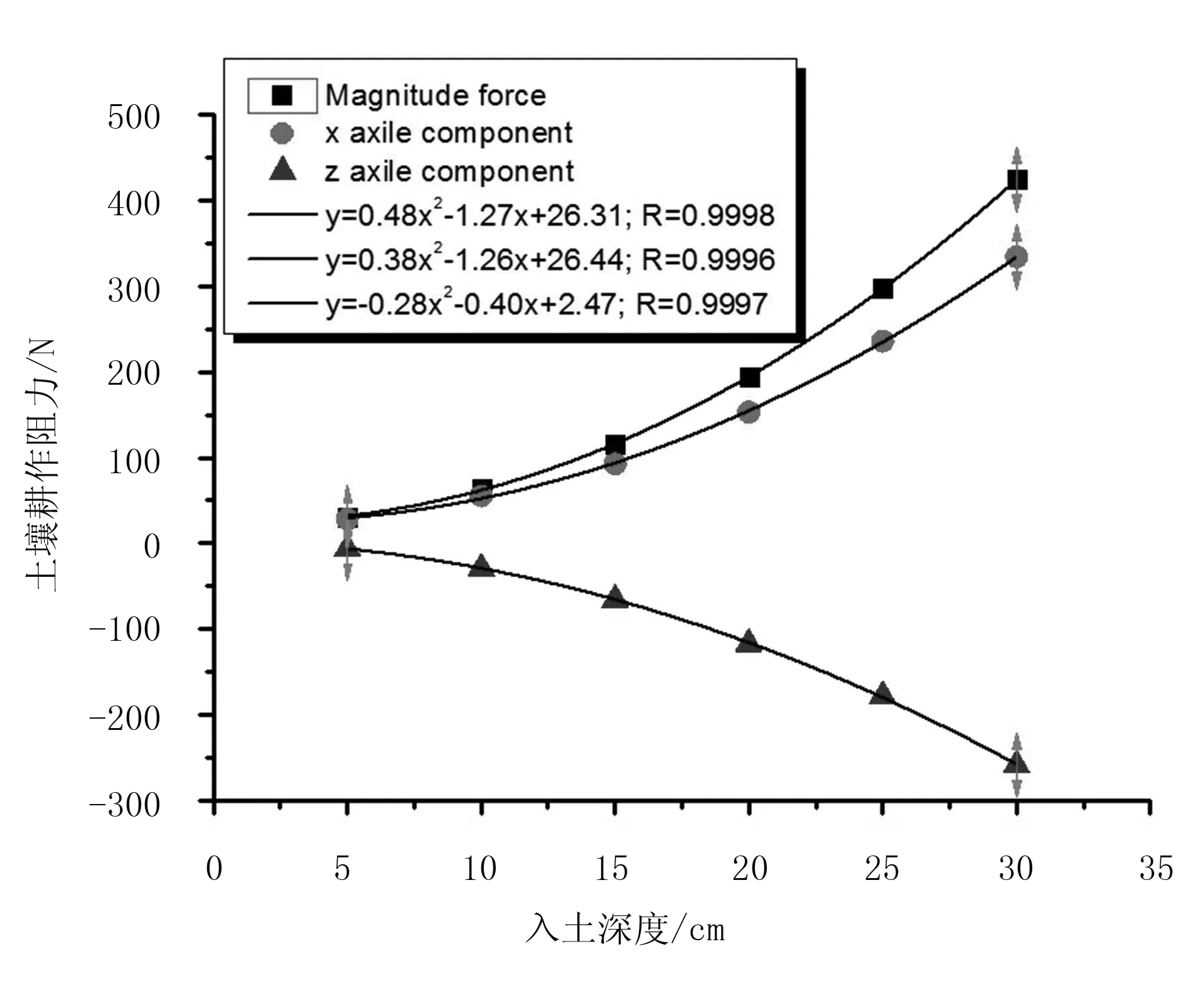
图5 深松铲土壤耕作阻力曲线Fig.5 Deep shovel soil tillage resistance curve

图6 载荷波动系数曲线Fig.6 Load fluctuation coefficient curve

利用Origin 8.0对表3数据进行曲线拟合，获得土壤耕作阻力MF及其前进分量XF、竖直分量ZF与

入土深度的拟合曲线方程及拟合相关系数分别为

(5)

各回归方程的拟合系数RMF=RXF=RZF=0.999≈1，说明回归方程拟合可靠。由图5可知：土壤耕作阻力MF及其前进分量XF为正值、竖直分量ZF为负值。这是由于深松铲为入土角为锐角，土壤对其有向下的作用；同时，土壤耕作阻力随着入土深度的增大而增大，但由于不同深度的土壤具有不同的土壤容重及土壤坚实度，造成耕作阻力与入土深度间并呈非线性关系。由图6可知：土壤耕作阻波动系数随着入土深度的增大而减小，表明随入土深度的加深，土壤耕作阻力的波动状况降低，尤其竖直分量波动状况降低更加明显。

2.2 作业速度的影响

为了分析作业速度对凿式深松铲土壤耕作阻力的影响，分别设定作业速度0.5、1.0、1.5、2.0、2.5、3.0m/s6个水平，其它参数设置不变；同样，提取每种试验处理下的稳定段绝对平均土壤耕作阻力MFa、前进分量XFa及竖直分量ZFa与波动系数λ。作业速度对土壤耕作阻力及载荷波动系数的影响如图7、图8所示。

土壤耕作阻力MF及其前进分量XF、竖直分量ZF与作业速度的拟合曲线方程及拟合相关系数分别为

(6)

各回归方程的拟合系数分别为RMF=0.984、RXF=0.985、RZF=0.956，回归方程拟合可靠。由图7可知，绝对土壤耕作阻力MF及其前进分量XF、竖直分量ZF随着作业速度的增大而增大，这是由于当速度增大时，单位时间耕作土壤量增大，铲面接触土壤颗粒的运动速度增大，造成更多的能量消耗，进而土壤耕作阻力增大。由图8可知，土壤耕作阻波动系数随着作业速度的增大而整体呈现增大趋势，但绝对土壤耕作阻力MF及前进分量XF的载荷波动在1.5～2m/s范围发生一次减小，而竖直分量ZF的波动减小则推迟发生在2～2.5m/s范围内。

图7 深松铲土壤耕作阻力曲线Fig.7 Deep shovel soil tillage resistance curve

图8 载荷波动系数曲线Fig.8 Load fluctuation coefficient curve

3 结论

应用EDEM分析了轻型凿式深松铲土壤深松作业过程的耕作载荷组成及入土深度与作业速度对土壤耕作载荷的影响，结果表明：深松铲土壤耕作阻力主要由前进阻力及垂直阻力决定，土壤耕作阻力及其前进、竖直分量随着作业速度及入土深度的增大而增大，且土壤耕作阻力与两作业参数间皆呈抛物线型二次函数关系；同时，土壤耕作阻力的波动状况随入土深度的增大及作业速度的减小而减小。该研究可为深松铲的设计研究提供一定的参考。

[1] 李洋阳，刘思宇，单春艳，等.保护性耕作综合效益评价体系构建及实例分析[J].农业工程学报，2015，31(15)：48-54.

[2] 陈源泉，隋鹏，高旺盛.不同方法对保护性耕作的生态评价结果对比[J].农业工程学报，2014，30(6)：80-87.

[3] 白景峰，李博，吕秀婷，等.基于狗獾爪趾的仿生深松铲结构设计与试[J].农机化研究，2016,38(4):175-179.

[4] 张强，张璐，刘宪军,等.基于有限元法的仿生钩形深松铲耕作阻力[J].吉林大学学报：工学版,2012,42(增刊1)：117-121.

[5] 李博，刘凡一，陈军，等.深松铲耕作阻力影响因素的离散元法仿真分析[J].农机化研究，2015,37(2):71-74.

[6] 王景立,刘选伟. 基于ANSYS Workbench的弧形深松铲模态分析[J].中国农机化学报,2015, 36(2):38-40.

[7] 王宏立，张伟.基于的Pro/E和ANSYS的深松铲有限元分析[J].农机化研究,2012,34(12):33-36.

[8] 齐关宇，刘林，赵艳忠，等. 深松铲入土深度及铲形对耕作阻力影响[J].农机化研究，2015,37(11):161-165.

[9] 边小雷，侯亚娟，赵梅，等. 离散元法及其在颗粒粉碎领域的应用现状[J].矿山机械，2015,43(6)：62-67.

[10] Mustafa Ucgul, John M Fielke, Chris Saunders. 3D DEM tillage simulation: Validation of a hysteretic spring (plastic)contact model for a sweep tool operating in a cohesionless soil[J].Soil and Tillage Research,2014,144:220-227.

[11] 季轩,黄世明,冯天玉,等.腐熟剂喷施装置出料部件数值模拟[J].中国农机化学报,2015,36(5):36-41.

[12] 李延民，韩枫钦，赵烨. 斜轴式高效混料机关键技术参数分析[J].机械设计与制造，2014(12):105-108.

[13] 陈志.农业机械设计手册[K].北京：中国农业科学技术出版社，2007:227-228.

[14] 王金武,王奇,唐汉,等.水稻秸秆深埋整秆还田装置设计与试验[J]. 农业机械学报，2015,46(9)：112-117.

[15] Mustafa Ucgul, John M Fielke, Chris Saunders. Three-dimensional discrete element modeling (DEM) of tillage: Accounting for soil cohesion and adhesion[J].Biosys tems Engineering ,2015,129:298-306.

[16] Aliakbar Solhjou, John M Fielke, Jacky M A Desbiolles. Soil translocation by narrow openers with various rake angles[J].Biosystems engineering,2012,112:65-73.

[17] Gao Qun, Chen Ying, Zhou Haibo, et al.Simulation of a seed opener using the discrete element method(DEM)[J].Agric Eng Int: CIGR Journal, 2015,17(3): 72-82.

[18] D.Karayel, A Ozmerzi. Comparison of vertical and lateral seed distribution of furrow openers using a new criterion[J].Soil & Tillage Research, 2007,95:69-75.

[19] Kornel Tamas，Istvan J Jori，Abdul M Mouazen. Modelling soil-sweep interaction with discrete element method[J].Soil and Tillage Research,2013,134:223-231.