基于GPU的RDF类型同构并行算法

冯佳颖 张小旺 冯志勇

1(天津大学计算机科学与技术学院 天津 300350) 2(天津大学软件学院 天津 300350) 3 (天津市认知计算与应用重点实验室 天津 300350) (fengjiaying@tju.edu.cn)

语义网(semantic Web)是一种新型的智能网络，它旨在解决当前Web上信息爆炸导致人们获取目标信息十分困难的问题.资源描述框架(resource description framework， RDF)和SPARQL查询语言是W3C(World Wide Web Consortium)组织推荐的用来描述语义网中的数据资源及其之间关系的语言规范和数据查询语言.随着RDF数据量的不断增大，如何在大规模RDF数据集上进行高效的查询检索是当今面对的一个重大挑战.

传统RDF数据集的查询方法使用CPU作为处理器，诸如Jena[1]，RDF-3X[2]，gStore[3]等集中式查询引擎系统，它们已将CPU的计算能力发挥到了极致.近年来，图形处理单元(graph processing unit, GPU)计算性能不断增强.由于GPU具有浮点计算能力强、带宽高、性价比高、能耗低等优势，可以极大地补充CPU的计算能力.利用GPU的并行处理能力实现算法和操作，可以大大降低CPU的负载.

在RDF数据集上的SPARQL(Simple Protocol and RDF Query Language)查询过程就是一个子图同构的过程.子图同构问题是图处理问题中一个最基本的研究内容，属于NP完全问题.类型同构是一种不精确的子图同构.通过顶点和边的标签约束，将部分查询转化为类型同构问题.并结合GPU数据处理方面高效的的计算性能，本文提出了使用并行硬件GPU实现对RDF类型同构查询的算法，从而提高RDF数据集的查询性能.

本文主要贡献如下：结合RDF数据的特征和GPU极高的计算能力，提出一种基于GPU的匹配算法，使GPU多处理器调度更简便；在GPU的硬件加速下，对本算法进行大量的性能实验.实验结果表明:基于GPU的类型匹配算法性能对于现有方法有了显著的提高.

1 背景知识

1.1 RDF和SPARQL

资源描述框架RDF是W3C组织提出的语义Web标准数据模型.它是用于形式化描述Web资源的元数据.RDF通过语法符号和序列化数据格式的方法来描述概念并对信息进行建模.RDF三元组(S，P，O)是RDF数据集的基本单元，一个RDF数据集中包含了许多RDF三元组，这些三元组表示了资源和资源之间的联系，其中S代表主语(subject),是被描述的资源，P代表谓语(predicate),表示资源的一个属性或关系，O代表宾语(object),表示属性值.

由许多RDF三元组组成的数据集将语义Web的信息表示成为一个带标注的有向图，称为RDF图.

定义1. RDF图.一个RDF图可以表示成为给定一个带标签的有向图G=(V，E，μ，σ).V表示顶点的有限集，E表示边的有限集.μ：V→LV表示顶点到顶点标签类型的映射函数.σ：E→LE表示边到边标签类型的映射函数.LV和LE是按标签排列的离散符号集合，表示了联系2个带标签的顶点或边的标签值向量.

Fig. 1 RDF graph图1 RDF图

如图1展示了一个RDF图，其中，椭圆节点表示资源，有向边表示属性，矩形节点表示字符值.例如，对于资源“me”，其“fullName”属性的值是一个字符值“Enic Miller”.

SPARQL查询语言是W3C组织推荐的RDF标准查询语言，由一组三元组模式(triple pattern)组成.大多数SPARQL查询都是由若干个基本图模式(basic graph pattern, BGP)组成.SPARQL查询即为图模式匹配，其查询的过程为找到与每个三元组模式匹配的三元组，再连接(join)具有共享变量的三元组模式的局部结果.结合图1，如果我们想获得某个具有属性“type”，同时具有属性“fullName”其值为“Eric Miller”的资源时，我们可以通过如下的SPARQL查询获得，其对应的查询图如图2所示.

SELECT ?xWHERE{

?xtype ?y.

?xfullName “Eric Miller”.}

Fig. 2 SPARQL query graph图2 SPARQL查询图

本工作通过研究SPARQL语法细节和语义的形式化定义[4]并使用GPU上的类型同构算法来提高特定基本图模式中查询处理的性能.

1.2 RDF中的子图同构与类型同构

依据RDF图是带标签的有向图的特征，本文的研究重点仅关注带标签的有向图.在已知的RDF数据中进行SPARQL查询的过程也就是一个模式图(即图2所示查询图)与RDF图的子图同构匹配过程.

定义2. 子图同构.给定一个RDF图G和一个模式图P，P包含n个顶点(v0，v1，v2，…，vn-1).如果G中包含n个顶点(u0，u1，u2，…，un-1)，与P之间存在一个单射函数f:P→G，使G的顶点和边与P的顶点和边一一匹配，则认为模式图P子图同构于有向图G.

寻找子图同构就是将模式图Gp嵌入RDF图G的过程.当子图的所有顶点、边都与模式图的排列顺序相同，并且对应的顶点和边符合各自的标签时，匹配过程结束.

定义3.k边游走.假设一个图中的非空有限序列W=(v0，e0，v1，e1，v2，…，ek-1，vk)，其中边ei连接顶点vi和vi+1.这个序列的长度为2k+1，被称为k边游走(k-edge walk).

定义4. 类型同构.给定一个RDF图G=(VG，EG，μ，σ)，和相关联的模式图P=(VP，EP，μ，σ)，它们之间存在标签函数的映射关系，μ:V→LV和σ:E→LE分别定义了顶点和边与标签之间的映射关系，其中LV和LE为标签集合，即LVP⊂LVG和LEP⊂LEG.定义P的k边游走为

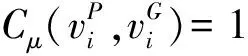
类型同构通过k边游走算法，计算出RDF有向图中与模式图的类型相匹配的部分.如图3(b)和图4(b)中虚线框内G的子图均为满足P的类型同构.不同之处在于图3(b)是对P的顶点不加约束的类型同构，图4(b)是对P的顶点增加约束的类型同构，说明类型同构只是匹配满足映射的顶点与边，并不要求同构.

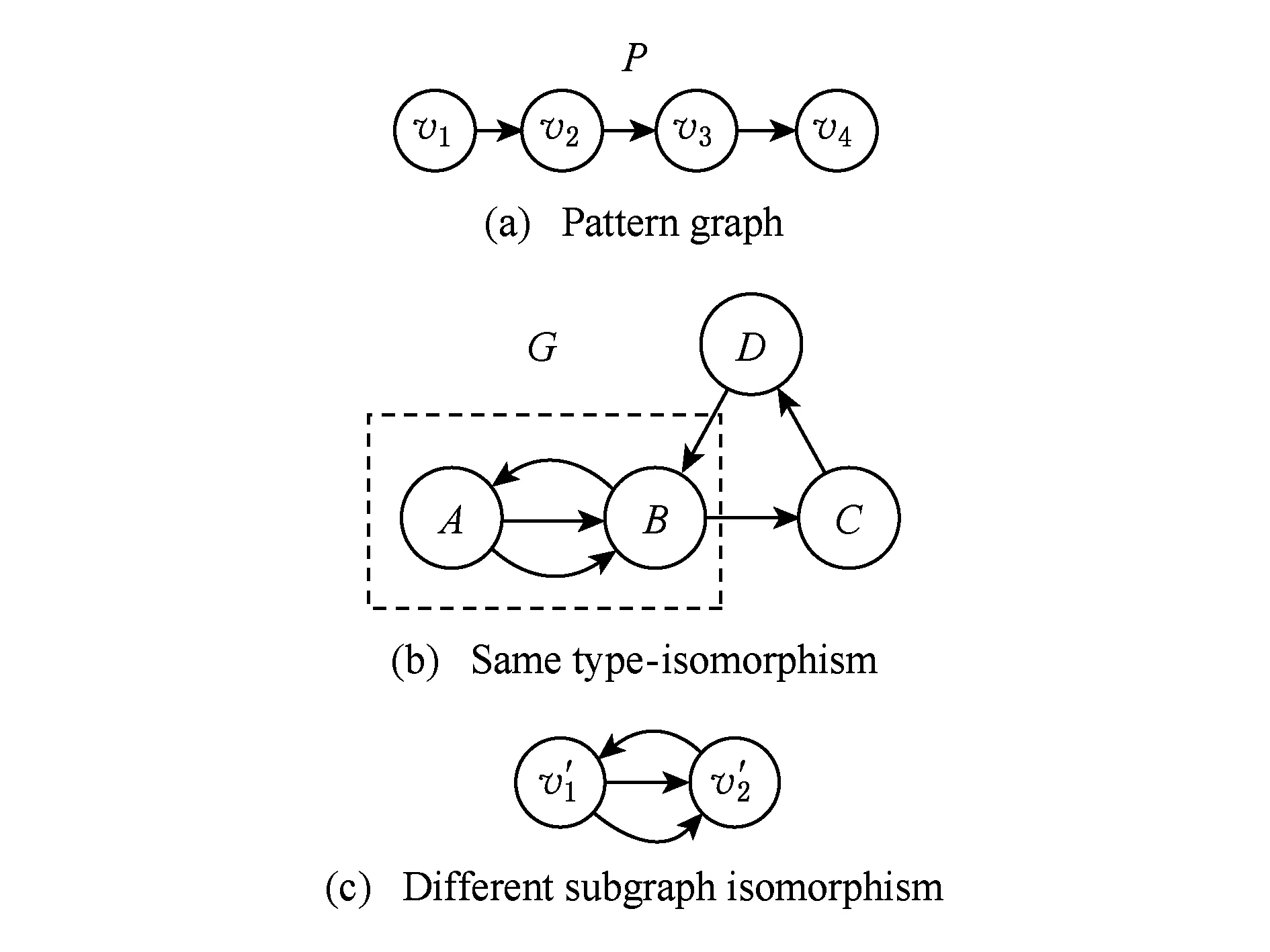
Fig. 3 Without constrained type-isomorphism of P vertexes 图3 P的顶点不加约束的类型同构

类型同构是一种不精确的子图匹配，不同于子图同构问题的是类型同构不需要找到同构结构.如图3(a)和图4(a)所示的G对应了相同的类型同构，但对应了不同的子图同构，如图3(c)和图4(c)所示.通过对类型同构的k边游走序列增加标签的限制，从而得到更精确的结果,如图3所示.IRSMG[5]中提出子图同构问题的解可以简化为约束的类型同构的解.因此，本文将在RDF图与基本图模式之间的匹配问题，转化为RDF图与相应的关联模式图的附加约束的类型同构匹配问题.

Fig. 4 Constrained type-isomorphism of P vertexes图4 P的顶点增加约束的类型同构

Fig. 6 Concurrent threads of GPU图6 GPU的并发线程

1.3 GPU架构和CUDA编程模型

图5所示为CPU与GPU架构示意图.与CPU相比，GPU增多了算术逻辑单元(arithmetic and logic unit, ALU)，使其更适用于规则结构、算法单一的数据处理.基于GPU的特征，本文设计了GPU多处理器的调度模型，以提高其计算性能.

Fig. 5 Architecture of CPU and GPU图5 CPU与GPU架构示意图

GPU由许多单指令多数据流(single instruction multiple data, SIMD)处理器组成，支持数千个并发线程，如图6所示为拥有GPU设备，Host为CPU控制端，Device为GPU设备端.Host端程序的执行按照串行代码(serial code)运行，图6左端箭头指示了程序串行执行的时间顺序.当内核(kernel)程序运行时，调用GPU进行计算，数以千计的GPU将同时进行计算，其组织形式如图6所示.GPU线程具有低上下文切换和低创建线程时间的特点.GPU的线程被组织为线程组(thread group).同一个线程组中的所有线程共享计算资源，例如寄存器、缓存等.线程组被分为多个调度单元方便在多处理器上动态调度.GPU内存具有高带宽和高访问延迟等特点，这些优势使GPU更适合于大规模RDF数据的并行计算.

CUDA(compute unified device architecture)是显卡厂商NVIDIA推出的一款用于GPU并行编程的编程模型API(application programming interface).在CUDA中，并行工作负载以计算内核(kernel)的形式表示并提交到设备上执行.内核的构造方式提供了细粒度并行性.通常在主机的CPU上控制内核的提交和执行.每个线程被分配唯一标识符，并为它们安排调度顺序.线程标识符常用于加载和存储的内存偏移量的计算.主进程和计算单元之间的数据传输通过全局存储器来完成，并且所有线程都有全局存储器访问权限.但是CUDA编程模型不提供计算单元的内存分配方法.这意味着在执行内核之前，主进程需要分配好所需的输出缓冲区.

结合RDF数据和GPU计算能力的特征，本文主要涉及的是为内核计算的编码和执行设计一个完善的GPU调度策略，并提出一种基于GPU的类型算法来提高部分基本图模式的查询效率.

2 相关工作

子图同构是精确的图匹配，是图数据研究中的一个NP-完全(NP-complete)问题.近年来，子图同构问题得到了广泛的关注,很多研究人员尝试了许多方法来解决通用图中的子图同构问题.1976年，Ullmann[6]第1次提出了实用的子图同构的搜索算法.该算法基于回溯的思想，当部分解决方案可行时对其进行迭代直到找出完整的解决方案；如果发现部分解决方案不可行，则及时终止.目前，已有一些方法对Ullmann算法进行改进，例如VF2[7]，QuickSI[8]，GraphQL[9]，GADDI[10]，SPath[11]等.这些算法利用不同的连接顺序、剪枝规则或辅助信息对候选集进行及时有效的剪枝筛选，从而减少连接操作的运算量，提高算法性能.但是，由于时间复杂度较高，这些算法不适用于大规模图数据的应用场景.

为了加速在大规模图或者多数量图上的子图同构操作，STwig算法[12]将查询图分解成一系列结构简单的基本单元，这些基本单元能够非常容易地在数据图中完成匹配，但是将产生的局部结果组合在一起则需要高效的连接策略.吕雪栋等人[13]设计的FFD-Inde是建立一种新颖的索引算法来加速星形图的查询处理.在星形查询中，这种方法在数据量巨大的情况下显著地提高了查询效率，但是星形查询只是查询图的一部分，无法推广到查询图的一般情况.基于类型同构的非精确子图同构是由精确子图同构问题的泛化引入的.这种方法比较新颖并且可以扩展到子图同构问题.Berry等人[14]提出了基于类型同构的不精确的子图同构问题.类型同构不需要像子图同构一样结构完全相同.根据RDF数据的特征，考虑利用顶点和边的标签的类型信息，将子图同构问题转化成为带约束的不精确的类型同构问题.

近些年，图形处理器GPU在并行处理方面取得了十分显著的成绩.由于计算能力强和便于编程，GPU已经逐渐发展成为用于通用计算中常用的协处理器[15].基于GPU的大规模并行处理框架已经成功应用于处理大规模图上的基本图操作，包括广度优先搜索[16]、最短路径[17]和最小生成树[18].在RDF数据管理领域，Pan等人[19]率先在RDFS中明确提出计算量的工作负载的概念从而允许利用GPU的细粒度并行，并以此获得性能的提高.该工作仅关注了RDFS推理的并行，没有关注在底层数据查询查询处理的优化.Choksuchat等人[20-22]提出一种基于Jena的RDF处理系统，存储结构使用基于Cassandra的Key-value结构和基于HDT的二进制三元组模式(binary triple pattern)，并实现了基于JCuda语义查询.Chantrapornchai等人[23]提出基于Bitstructure的修剪算法处理查询并使用概要信息以减少数据读取量的方法，以保证可扩展性和优化内存使用状况.TripleID[24]是用于RDF查询和推导处理的并行框架，它提供了一种新颖的压缩RDF数据的文件格式，以通过GPU并行加速数据处理.Fu等人在2014年提出的MapGraph[25]是基于对PowerGraph’s Gather-Apply-Scatter(GAS)模型的修改而实现的.他们使用MapGraph实现了4种常见的图形分析操作：宽度优先搜索(BFS)，单源最短路径(SSSP)，连接组件(CC)和PageRank(PR).2015年，Yang等人[26]提出了在普通图上进行并行处理子图同构的GPU算法，但普通图的规模有很大的局限性[27]，例如语义信息含量少、节点数量少等[28]，所以此方法并不适用于大规模的RDF数据[29].同样，对于处理大规模的RDF数据的类型同构问题也没有高效的基于GPU的求解方式.

这些方法的共同之处在于将RDF三元组进行编码压缩，并对其建立索引，以加速存储查询的过程.本文依据RDF图数据的特性，提出一种基于类型同构的子图匹配算法，以使GPU并行计算应用于在RDF图处理，并提高子图匹配的性能.

3 RDF类型同构算法

3.1 字典构建

本文选择以串行的方式解析文件和预处理数据.依据RDF数据的特性，每个三元组元素都由主语、谓语和宾语3部分组成，并且每个元素都是字符串(string)值，例如URI(uniform resource identifier)或字符值.程序在内存中构造字典将所有字符串值转化为整数值.这样保证了每个值都是固定长度，方便后续程序对数据进行处理.同时，由于缓冲区需要在数据传输前进行分配，固定长度可以降低GPU调用的的复杂度，提高算法的性能.

字典是在CPU中动态构建的.本算法使用散列映射(Hash map)建造字典.散列映射是一个关联容器，用于关联Key类型的对象与Data类型的对象.散列映射中可以高速查找Key值元素，本算法利用这一优势来查找字典中的无序三元组.字典可以简便地加载到内存或存储在磁盘文件中.在解析三元组时，主语和宾语均描述的是资源，算法对其进行相同的处理.谓词作为资源的连接关系需要单独处理，并将三元组扩展成了五元组G=(S，P，O，μ，σ).μ映射表示标签值与每个顶点(即主语和宾语)的关系，σ映射表示标签值与每个边(即谓语)的关系.

3.2 基于GPU的类型同构算法

基本图模式查询是SPARQL查询的基本形式和主要子集[19].SPARQL中的其他图模式，如联合模式(union graph pattern)、可选模式(optional graph pattern)等，都可以通过额外的代数运算转换为基本图模式.

由2.2节中描述的概念，类型同构根据已形成的游走路径WP来访问RDF中顶点和边.理想情况下，查询包含用作最小游走长度的欧拉路径.如果查询是可以由欧拉路径构造的基本图模式查询，并且在顶点和边添加标签约束，那么类型同构的解就是基本图模式查询的解.但是在实际情况中，基本图模式查询都是有向无环图.因此，查询可能无法追踪任何的满足欧拉路径的游走路径而导致失败.

1) 基于GPU的并行映射算法.第2节中讨论过GPU和CUDA编程模型的特性.由于GPU在代码的执行期间不支持在设备上动态分配内存.所以需要利用设计好的数组结构在执行GPU程序之前为输入数据和输出结果分配空间.当GPU执行映射操作时，如果三元组满足映射条件，则将候选三元组Etp放置在输出缓冲器中；如果不满足映射条件，则需要为输出缓冲器设置额外的空间以存储中间结果.因此，将所有数组结构中的元素初始设置为0，在缓冲区根据主语ID排序，以减少三元组主语ID的重复.

2) 基于GPU的连接算法.连接是将多个已匹配的局部匹配图合并为完整匹配图的操作.如果基本图模式包含共享变量，那么就将映射的输出直接传递到连接中.如果基本图模式没有共享变量，则无法进行接下来的连接操作.那么对于类型同构来说，如果2个匹配的三元组有1个共享变量，那么它们可以被合并成1个通路.

为了充分利用GPU并行的优点，连接过程包含3个阶段：①并行映射;②按ID排序;③去重.在并行映射阶段中，本算法根据共享变量在三元组中的位置设置标志以减少去重阶段的冗余操作,而GPU的单指令多数据的体系架构特点也有助于加速笛卡儿乘积的平行化.

本文提出的算法请见算法1，是以初始化游走列表InitWalks开始，以选择RDF数据图中第1个可以与WP模式匹配的分段.从行②开始的循环，每次迭代都会通过匹配分段，进一步扩大候选集的游走长度的范围.映射操作输出分段并以顶点ID作为关键字(Key).行③说明了匹配的实现，并且本算法使用双调排序法(bitonic sort)对映射操作的结果进行并行排序.其作用是通过共享变量顶点的关键字对游走的候选集进行排序.算法1的其余部分是通过对计算笛卡儿积而实现去重操作.算法1通过1次迭代WP的一个分段以构建与该分段匹配的所有游走的候选集.显然，生成结果中完整长度的有向路径的集合即是所有类型同构游走的结果集合，也就是在RDF数据图中完成了类型同构的匹配过程.

算法1. 基于GPU的类型同构算法.

输入：RDF数据图中所有三元组模式的集合S、将图分段成k个有序列表TP；

输出：在RDF中完成匹配的集合R.

① InitWalks：接收S和TP从S中读取分段s；

② ifs能够匹配WP中的第1个分段(S1，P1，O1)

③ 将S添加入candidate walk为1的候选集中；

④ ExtendWalks：

⑤ for每一个Key值小于k的记录do

⑥ 从S中读取另一个分段s.如果它能够匹配WP中的第1个分段(St,Pt,Ot)，将s添加入游走长度为t的候选集中，并从最近访问的候选集中读取candidate walk；

⑦ end for

⑧ 使用双调排序发对candidate walk进行并行排序；

⑨ for每个定点do

⑩ whileCandWalkList的每个成员

4 实验设计和性能分析

本节在GPU架构上实现了RDF图上的类型同构算法，并对其进行了性能测试.经过与CPU架构下的类型同构算法的效率对比，并将gStore中基于子图同构的方法与本文中的算法进行比较，证明了GPU架构解决类型同构问题的效率优于CPU架构，进一步说明GPU在解决RDF数据查询问题上具有突出的性能.

4.1 CPU与GPU的比较实验

1) 实验环境和数据集

本实验平台的配置为NVIDIA GTX590 1.35 GHz GPU的显卡和运行英特尔®Core(i)i7-26 001.35 GHz的4核处理器.操作系统版本为Linux Ubuntu 14.04，内存大小为2 GB，GPU的设备内存为1 536 MB.GPU使用PCI-E3.0总线在主存储器和设备存储器之间进行数据传输数据，其传输带宽为4 GB/s.

实验采用LUBM(Lehigh University Bench-mark)数据集.LUBM是一个采用大学领域内本体的基准，可以生成任意大小的OWL数据类型.这些数据中包含了教师、学生、课程等信息之间的关联信息.由于本算法关注的是RDF数据的图匹配问题，需要对产生的OWL数据进行预处理，将其转化为系统处理所需的RDF三元组格式.本实验选取了7个不同规模的LUBM数据集来测试算法的性能.表1详细描述了这7个数据集的数据特征和规模.为了对本文提出的算法进行测试与分析，本实验选取了2种查询方案，如表2所示.

Table 1 LUBM Datasets of Experiment表1 实验使用LUBM数据集

Table 2 Benchmark Test Queries表2 基准测试查询语句

2) CPU与GPU实验结果和分析

本文选取了LUBM查询中具有代表性的查询语句作为实验的基准测试查询，分别对7个不同规模的数据集上进行测试，以比较相同环境下CPU和GPU的性能.表3和表4中分别记录了每个查询仅使用CPU计算单元计算类型同构匹配算法的响应时间、使用基于GPU计算单元加速类型同构匹配算法的查询响应时间、以及它们之间的加速比.表3和表4中的查询响应时间均为多次测试后的平均响应时间.本实验所测试的算法查询响应时间仅包括从用户提交查询到查询结束之间的时间，不包括数据的载入时间和数据IO的传输时间.

Table 3 Query Response Time of Q1 over LUBM Datasets表3 Q1在LUBM数据集上的查询响应时间 ms

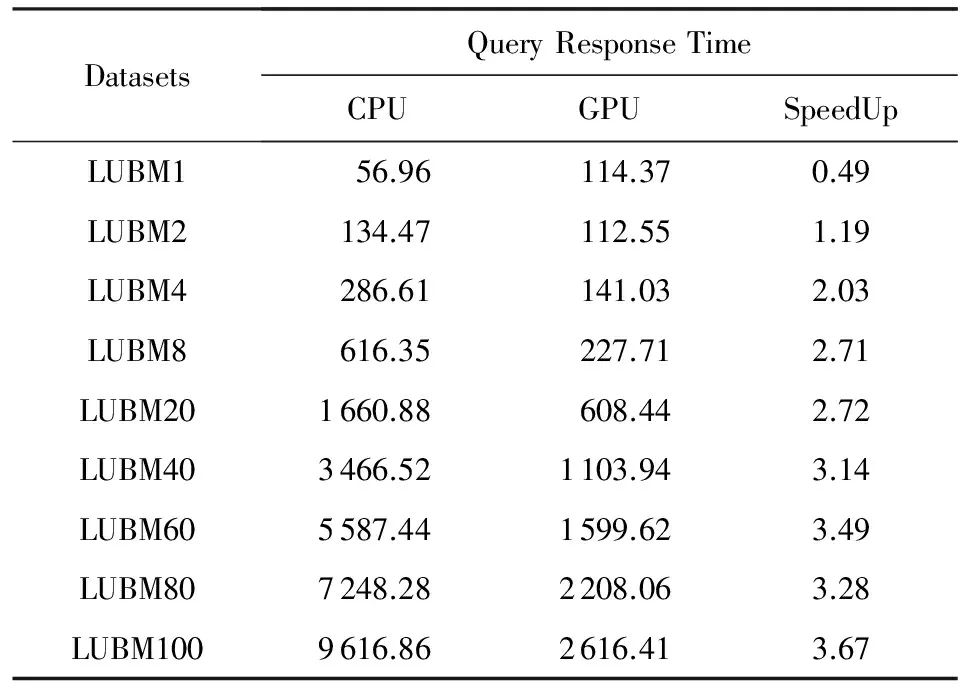
Table 4 Query Response Time of Q2 over LUBM Datasets表4 Q2在LUBM数据集上的查询响应时间 ms

图7(a)为查询Q1在不同规模LUBM数据集上的查询响应时间，图7(b)为基于CPU的查询响应时间与基于GPU查询的加速比.图8则分别为查询Q2在不同规模LUBM数据集上的查询响应时间和基于CPU的查询响应时间与基于GPU的加速比.

由实验结果分析，在数据量较少的情况下，例如LUBM1，本算法的查询响应时间与基于CPU的算法的时间近似.原因是在初始化时CPU调用GPU进行数据分配调用的过程需要额外耗费一定通信代价.但是随着数据集的不断增大，由于GPU并行计算能力强，GPU的查询响应时间远远低于CPU的运行时间.图7和图8所示，随着数据量的不断增大，GPU的查询响应时间明显低于CPU.且CPU和GPU的加速比随着数据量的增大而逐渐上升，最后稳定在3倍左右.说明在类型同构并行算法中，GPU的查询效率远高于CPU.

Fig. 7 Query response time and speedup between CPU and GPU of Q1图7 Q1的查询响应时间及CPU与GPU运算的加速比

Fig. 8 Query response time and speedup between CPU and GPU of Q2图8 Q2的查询响应时间及CPU与GPU运算的加速比

对比实验结果数据，本文提出的基于GPU的RDF类型同构的并行算法性能显著高于CPU处理的性能.

4.2 类型同构与子图同构算法比较结果和分析

1) 实验环境和数据集

本实验平台的配置有NVIDIA Tesla M40 GPU的显卡和运行英®Xeon®E5-2603 v4 1.7 GHz的6核处理器.操作系统版本为Linux Ubuntu 14.04 Server，内存大小为8 GB，GPU的设备内存为24 GB.本实验使用数据集及查询语句如表5和表6所示.

Fig. 9 Query response time and speedup between CPU and GPU of Q3图9 Q3的查询响应时间及CPU与GPU运算的加速比

DatasetsTripleNumberDatasetsSize∕MBEntityLUBM101316700160．56207443LUBM202782126341．41437572LUBM304109002505．10645971LUBM405495742676．19864239LUBM506890640848．32137216LUBM100138799701711．102179783

Table 6 Benchmark Test Queries表6 基准测试查询语句

为了与4.1节中实验区分，本文选取了LUBM查询中的较为复杂的查询语句(作为实验的基准测试查询，分别对8个不同规模的数据集上进行测试.比较相同环境下基于子图同构的RDF数据查询引擎与本文所提算法性能.

2) CPU与GPU实验结果和分析

本文选取了LUBM查询中具有代表性的查询语句作为实验的基准测试查询，分别对7个不同规模的数据集上进行测试.

表7和表8中的记录了Q3和Q4的查询响应时间与加速比.并在图9和图10中以图表形式分别进行展示.

Table 7 Query Response Time of Q3 over LUBM Datasets表7 Q3在LUBM数据集上的查询响应时 ms

Table 8 Query Response Time of Q4 over LUBM Datasets表8 Q4在LUBM数据集上的查询响应时间 ms

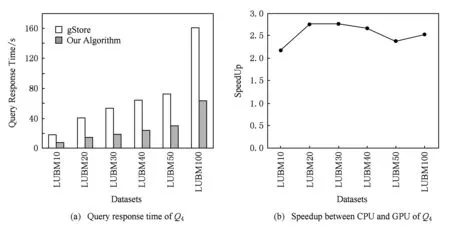
Fig. 10 Query response time and speedup between CPU and GPU of Q4图10 Q4的查询响应时间及CPU与GPU运算的加速比

由图表分析所得，本实验所提方案与目前性能较好的集中式查询引擎gStore进行比较.与gStore相比，Q3的加速比约在1.4～1.9倍，本算法查询响应时间仅为其响应时间的1/2左右.Q4的加速比约在2.1～2.7倍，本算法查询响应时间仅为其响应时间的1/3左右.本算法总体性能提高了1.4～2.7倍.随着数据量的增大，本实验所提方案提升的性能显著.

经过查询对比发现，本算法在包含链状的查询(如Q1和Q4)，展现了良好的性能.但是在只含有星状查询(如Q3)中，其查询性能则略低于包含链状的查询.结合本文的理论基础分析，算法在星状查询中展开成k边游走的过程中可能导致边的重复遍历，因而导致了算法的性能有所下降.

通过对比实验，本文提出的基于GPU的RDF类型同构的并行算法性能显著高于基于CPU的RDF子图同构的处理方法.

5 总 结

依据RDF图本身的数据特征，传统的子图同构的问题可以用来解决SPAQRL中基本图模式查询问题.本文基于IRSMG的方法和理论，提出了一种基于GPU的RDF类型同构并行算法，以高效地完成基本图模式查询，减少查询响应时间.本文通过研究约束的类型同构问题，将问题引申至RDF图的模式匹配和查询.通过设置游走等级的方法，对满足查询图标签的顶点进行遍历检查，确定后续查找范围.最后得到每个三元组模式的局部解，使用GPU并行的进行连接操作.因此最大程度利用了GPU的计算能力，使基本图模式查询性能有了显著的提高.

尽管本工作研究的问题仅限于基本图模式查询，但是其性能优于CPU的处理方式.这为以后RDF数据处理的发展提供了新的思路.由于现在本文所提出的算法仅能支持部分基本图模式，例如涉及星状和链状的查询，对于包含环状的查询则体现了较为一般的性能.因此如何将本算法的思想推广到基本图模式一般情况将是本文后续工作.

[1] Mcbride B. Jena: Implementing the RDF model and syntax specification[C] //Proc of the 5th ISWC’01. New York: ACM, 2001: 23-28

[2] Neumann T, Weikum G. RDF-3X: A RISC-style engine for RDF[J]. VLDB Journal, 2008, 1(1): 647-659

[3] Zou Lei, Özsu M, Chen Lei, et al. gStore: Answering SPARQL queries via subgraph matching[J]. VLDB Journal, 2014, 23(4): 565-590

[4] Pérez J, Arenas M, Gutierrez C. Semantics and Complexity of SPARQL[M]. Berlin: Springer, 2006: 1-45

[5] Zhang Junzhao, Zhang Bingyi, Zhang Xiaowang, et al. IRSMG: Accelerating inexact RDF subgraph matching on the GPU[C] //Proc of ISWC’16. Berlin: Springer, 2016

[6] Ullmann J. An algorithm for subgraph isomorphism[J]. Journal of the ACM, 1976, 23(1): 31-42

[7] Cordella L, Foggia P, Sansone C, et al. A (sub) graph isomorphism algorithm for matching large graphs[J]. IEEE Trans on Pattern Analysis and Machine Intelligence, 2004, 26(10): 1367-1372

[8] Shang Haichuan, Zhang Ying, Lin Xuemin, et al. Taming verification hardness: An efficient algorithm for testing subgraph isomorphism[J]. VLDB Journal, 2008, 1(1): 364-375

[9] He Huahai, Singh A. Graphs-at-a-time: Query language and access methods for graph databases[C] //Proc of ICDM’08. New York: ACM, 2008: 405-418

[10] Zhang Shijie, Li Shirong, Yang Jiong. GADDI: Distance index based subgraph matching in biological networks[C] //Proc of EDBT’09. New York: ACM, 2008: 405-418

[11] Zhao Peixiang, Han Jiawei. On graph query optimization in large networks[J]. VLDB Journal, 2010, 3(1-2): 340-351

[12] Sun Zhao, Wang Hongzhi, Wang Haixun, et al. Efficient subgraph matching on billion node graphs[J]. VLDB Journal, 2012, 5(9): 788-799

[13] Lyu Xuedong, Wang Xin, Li Yuanfang, et al. FFD-Index: An efficient indexing scheme for star subgraph matching on large RDF graphs[G] //LNCS 9052: Proc of Database Systems for Advanced Applications. Berlin: Springer, 2015: 240-245

[14] Berry J, Hendrickson B, Kahan S, et al. Software and algorithms for graph queries on multithreaded architectures[C] //Proc of IPDPS’07. Los Alamitos, CA: IEEE Computer Society, 2007: 1-14

[15] Xu Xinhai, Lin Yufei, Yi Wei. A survey of techniques of CPU-GPGPU heterogeneous architecture[J]. Computer Engineering & Science, 2009, 31(S1): 24-26 (in Chiness)

(徐新海, 林宇斐, 易伟. CPU-GPGPU异构体系结构相关技术综述[J]. 计算机工程与科学, 2009, 31(S1): 24-26)

[16] Merrill D, Garland M, Grimshaw A. Scalable GPU graph traversal[J]. ACM Sigplan Notices, 2012, 47(8): 117-128

[17] Katz G, Kider J. All-pairs shortest-paths for large graphs on the GPU[C] //Proc of GH’08. New York: ACM, 2008: 47-55

[18] Vineet V, Harish P, Patidar S, et al. Fast minimum spanning tree for large graphs on the GPU[C] //Proc of HPG’09. New York: ACM, 2009: 167-171

[19] Heino N, Pan J. RDFS Reasoning on massively parallel hardware[G] //LNCS 7649: Proc of ISWC’12. Berlin: Springer, 2012: 133-148

[20] Choksuchat C, Chantrapornchai C. Large RDF representa-tion framework for GPUs case study key-value storage and binary triple pattern[C] //Proc of ICSEC’2013. Piscataway, NJ: IEEE, 2013: 13-18

[21] Choksuchat C, Chantrapornchai C. Experimental framework for searching large RDF on GPUs based on key-value storage[C] //Proc of JCSSE’13. Piscataway, NJ: IEEE, 2013: 171-176

[22] Choksuchat C, Chantrapornchai C. On the HDT with the tree representation for large RDFs on GPU[C] //Proc of the 19th ICPADS’13. Los Alamitos, CA: IEEE Computer Society, 2013: 651-656

[23] Chantrapornchai C, Choksuchat C, Haidl M, et al. Entailment processing for large RDF data sets using GPU[C] //Proc of SoMeT’16. Clifton, NJ: IOS, 2016: 333-345

[24] Haidl M, Gorlatch S. TripleID: A low-overhead represen-tation and querying using GPU for large RDFs[C] //Proc of BDAS’16. Berlin: Springer, 2016: 400-415

[25] Fu Zhisong, Personick M, Thompson B. MapGraph: A high level API for fast development of high performance graph analytics on GPUs[C] //Proc of GRADES’14. New York: ACM, 2014: 1-6

[26] Yang Bo, Lu Kai, Gao Yinghui, et al. GPU acceleration of subgraph isomorphism search in large scale graph[J]. Journal of Central South University, 2015, 22(6): 2238-2249

[27] Fu Lizhen, Meng Xiaofeng. Reachability indexing for large-scale graphs: Studies and forcasts[J]. Journal of Computer Research and Development,2015, 52(1): 116-129 (in Chiness)

(富丽贞, 孟小峰. 大规模图数据可达性索引技术：现状与展望[J]. 计算机研究与发展, 2015, 52(1): 116-129)

[28] Zou Lei, Peng Peng. A survey of distributed RDF data management[J]. Journal of Computer Research and Development, 2017, 54(6): 1213-1224 (in Chiness)

(邹磊, 彭鹏. 分布式RDF数据管理综述[J]. 计算机研究与发展, 2017, 54(6): 1213-1224)

[29] Li Jianhui, Shen Zhihong, Meng Xiaofeng. Scientific big data management: Concepts, technologies and system[J]. Journal of Computer Research and Development, 2017, 54(2): 235-247 (in Chiness)

(黎建辉, 沈志宏, 孟小峰. 科学大数据管理: 概念、技术与系统[J]. 计算机研究与发展, 2017, 54(2): 235-247)