数学课堂巧用错误资源摭谈

张秀花

【摘要】数学课堂巧用错误资源，挖掘错误背后的有效教学因素，丰富教学内容。以误导正，让错误成为学生认知的“转折点”，思维飞跃的“起跳板”，互学共进的“融合剂”，打造“学”的课堂，让儿童的数学学习真实发生。

【关键词】课堂教学；数学思维；错误；生成

英国心理学家贝恩布里奇说过： “错误人皆有之，作为教师不利用是不可原谅的。”数学课堂教学中，学生的错误真实地反映了学生的疑惑和误解，作为教师，我们需要把错误看作有效的课堂教学资源，善于引导学生识“错”、 析“错”、思“错”、悟“错”，激发探究的兴趣，点燃思维的火花，对概念进行正确理解并深化，从而将错误纠正过来，将它变成宝贵的学习资源，让“错误”成为“正确”的先导。

一、巧用错例，以错导学

哲学家黑格尔先生说得好：“错误本身乃是达到真理的一个必然的环节。”真实的数学课堂，学生出错是司空见惯的情况，教师要适时、巧妙地分析引导，引发认知冲突，这能有效激发学生探究新知的兴趣。如一位老师教学“平均数”，新课伊始，创设套圈游戏，教者依次呈现男生和女生各1名、男生和女生各2名、男生和女生各3名、男生和女生各4名的套圈成绩，学生均能用比多、比少、比总数，得出男女生的套圈成绩。最后，教者呈现4名男生和5名女生的套圈成绩统计图（如右图），提出问题：男生套得准一些还是女生套得准一些，怎么比较呢？问题在学生中引起了不同意见的争论，有的认为比较男生和女生中套得最多的个数，有的认为比较男生和女生套中的总个数。教者顺势而导，启发学生思考，你认为哪种比较方法是合理的？学生再次产生争论，发现两种比较方法都不合理，产生探究新知的心理需求，思考合理有效的比较方法，进而引入“平均数”这一新概念的学习。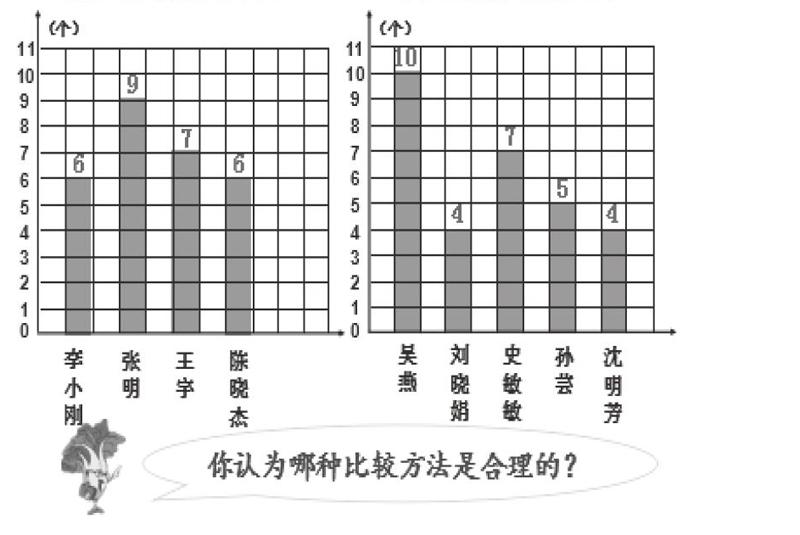

下面仍以“平均数”为例，学生要有效建构“平均数”的新概念，离不开练习的巩固与应用，教师就应为学生提供一些有益于突破知识难点的典型错例，让学生识别错误，针对错误要点，引导学生进一步加深对知识的理解与掌握。这里，教者在学生初步理解平均数的含义及掌握求平均数的方法后，引入一组生活中的实例让学生比较辨析：①王力是学校足球队员，他身高145厘米，可能吗？学校足球队可能有身高超过150厘米的队员吗？②小军想下水学游泳，池塘的平均水深100厘米。小军问：“我身高145厘米，下水游泳有危险吗？”你们觉得他下水游泳有没有危险呢？③小兵走6步，共走了330厘米，他每一步都走了55厘米，对吗？④电梯里有5人，他们体重的和是310千克，每个人的体重都是62千克，对吗？通过典型的错例，教师可以引导学生展开讨论，运用所学的平均数的知识判断和分析对错，体会平均数只是代表一组数据的整体水平，实际数值可能远远高于平均数，也可能低于平均数，加深学生对平均数实际意义的理解。

二、巧用错解，以错助学

布鲁纳说过：“学生的错误都是有价值的。”数学课堂中出现的错误，有的是学生最初的思维展现，有的是学生最真的思维流露，教师应善于发现与捕捉学生的错误，点燃学生思维碰撞的火花，有效促进学生分析、比较、判断、推理等思维能力，实现教学的最佳功效，不能漠视学生的错误抑或视而不见，错失良机，需因势利导，有目的、适度地展示与“放大”有价值的错误，组织与引导学生议错、辨错，聚焦知识的重点，突破学习的难点，有助于提升学生的思辨能力，促进数学思维的发展。

如一位老师在教学“不含括号的混合运算”时，让学生尝试计算350+180÷6×5后，先集体反馈正确的计算过程，接着展示收集到的典型的错解，具体如下：

教者引导学生自主辨析错误，找出并划出错误，想想哪儿出错了，弄清错因，紧扣混合运算的顺序这个关键问题，让学生在辨析错误、纠正错误的过程中，强化认识，加深印象。

再如运用商不变的规律计算被除数和除数末尾都有0的三位数除以两位数时，一位老师呈现如下问题：幼儿园阿姨带900元买洗衣液，如果每瓶50元，可以买多少瓶？如果每瓶40元，可以买多少瓶，还剩多少元？学生在解决第一个问题时，会用简便方法计算900÷50 =18（瓶）。这里的第二个问题，既是巩固商不变规律的简便方法，同时引出本课的知识难点：运用商不变的规律计算被除数和除数末尾都有0的三位数除以两位数时，余数究竟是多少？教者放手让学生自主尝试，有的学生竖式计算过程如下：900÷40=22（瓶）……2（元）

教者让学生交流自己的计算过程，无形中“放大”错误，引发学生辨析：余数究竟是2还是20呢？这时，有学生提出可以用验算的方法检验得数是否正确，教师让学生“将错就错”进行验算，发现22×40+2的得数不是900，而22×40+20=900，引导学生主动发现结果有错，并进行错误的合理修正。接着，教者抓住关键知识点，进一步追问“为什么余数是20而不是2呢？”激活学生的数学思维，学生结合自己已有的认识，再次思考和辨析“商不变，余数变”，运用商不变的规律，自主解释算理，进而知其然并知其所以然。

三、巧用错思，以错促学

杜威曾说过：“失败是有教导性的，真正懂得思考的人，他从失败和成功中学到的一样多，甚至更多。”数学课堂教学过程中，引导学生反思错误与自我诊断，主动分析错误的深层次原因，是学生的数学思维不断历练、生长和提升的过程。教师不必急于指出学生的错误，催学生“被動”纠错，不妨稍等片刻，把问题抛给学生，给学生多留一些自主究“错”、反思的时间和空间，促使学生自我反省、剖析错误，在“思维风暴”中获得更多的启迪、顿悟，感悟数学思考的成功与快乐。教师应巧妙引导学生回顾与剖析自己的思维过程，找出错误原因，及时内化感悟新知，唤醒数学思维的重组，修正错误的认知，正确建构新知。

如一位老师教学“3的倍数的特征”，课一开始，老师就让学生猜3的倍数有什么特征？有学生说看数的个位作判断，有学生接着补充说“我们已经学过个位是0或5的数是5的倍数，个位是0、2、4、6、8的数是2的倍数。那么个位上是3、6、9的数是3的倍数”。因为学生在前一节课已经学习了“2和5的倍数的特征”，因此纷纷猜想“个位上是3、6、9的数是3的倍数”也就情有可原了，这是学生受到思维定式的影响，基于2和5倍数的特征影响到3的倍数特征的判断。尽管有许多同学认同上述猜想，但也有同学发现猜想是错的，并举例23、26、29等数都不是3的倍数。这时，教者不置可否，而是把思考悟错的机会留给学生，用期待的目光扫向学生，鼓励他们积极动脑，然后做出评判。教者启发学生思考：“既然不能从个位上猜想3的倍数的特征，那怎样才能找出3的倍数的特征呢？”激发学生探究欲，燃起学生探究的热情。学生已有探索规律的数学活动经验，教者适时进行引导，让学生再次经历“猜想、举例、验证”的探究学习过程，学生通过大量举例发现“这样不行……”，继而思考“为什么不行”？那么“怎样才行……”继而思考“为什么这样行”？学生再通过举例验证，并注意进行及时的修正，最终探索出3的倍数的特征“各位上数字的和是3的倍数”。

总之，课堂教学是师生互动、生生互动的多维度动态过程，课堂教学是“一个生动活泼的、主动的和富有个性的过程”，在这一过程中，学生所学的数学知识是全新的，需要经历一个从未知到已知的过程。因此课堂上会出现很多始料未及的错误。其实学生出错是正常的，关键看我们怎样来对待它，让数学课堂变得更有意义，更有生命力，更精彩。学生的学习错误产生于学习活动中，亦可“消化”于学习活动中，作为教者的我们应因势利导为学生创造发现错误、改正错误的机会，让错误成为学生认知的“转折点”，让错误成为学生思维飞跃的“起跳板”，让错误成为互学共进的“融合剂”。因此教师应以发掘资源的眼光看待错误，巧妙地利用错误甚至可以故意布设错误，夯实数学的课堂教学。为此，教学时，我们应巧用这些错误资源，引导学生进行探究，从而有效激活数学课堂。诚然，引导学生识错、思错、悟错、纠错，体现了学生对错误的再认识、再思考，这些有价值的错误均是教学中重要的生长点，值得巧妙用好、用实、用活。在学生自主诊断、修正错误后，教师及时引领学生分析梳理、总结概况，挖掘错误背后存在的数学问题，形成正确的数学概念思想方法等，有效提升数学思维能力。