一类抛物方程猝灭解的数值计算B方法
霍冠泽, 林亭秀, 王林君
(1. 吉林大学 数学学院, 长春 130012; 2. 江苏大学 理学院, 江苏 镇江 212013)
1 预备知识
1.1 解的猝灭现象
半线性抛物方程解的猝灭问题在工业生产、 弹性体的断裂过程研究[1]及化学催化反应和酶反应的动力学描述[2]等领域应用广泛, 它反映燃烧过程以及火箭燃料在爆炸过程中的稳态与不稳态之间的转换现象, 对于猝灭条件的研究有利于构建最佳的燃烧环境, 了解更精确的燃烧过程[3].
本文考虑如下抛物问题猝灭解的数值计算方法:
(1)

定义1令u=u(t,x)是方程(1)定义在t>0,x∈Ω上初值问题的解,Ω⊂m是有界区域, 如果‖ut‖∞在有限时间T处趋于无穷, 则称解u具有猝灭现象, 此时T定义为猝灭时间.
由定义1可知, 方程的解是否表现出猝灭现象的决定条件是u对t导数的最大模是否在猝灭时间处趋近于+∞, 而并不是u是否在猝灭时间处趋近于0, 例如问题(1)的解在时间接近猝灭时间时, 解u→1.
1.2 B方法
解发展方程数值解的B方法[12]用来解决带有爆破现象的半线性发展方程. 传统的时间迭代方法, 如方程ut=Δu+F(u)向后Euler格式:
un+1-un=h(Δun+1+F(un+1)),
其中:un+1表示u(tn+1);h表示时间步长. 其数值解的收敛速度依赖于u和u的导数大小, 而这两项在爆破时间附近时至少有一个非常大, 因此数值解的收敛速度很慢, 有时对于给定的时间步长h甚至不收敛, 而B方法很好地克服了上述问题.
假设常微分方程ut=f(u)的精确解已知, 考虑扰动方程:
ut=f(u)+εl(u),
(2)
其中εl(u)为空间微分项, 即扰动项. B方法是在解非线性常微分方程变异系数法的基础上进行修正得来的, 适用于解方程(2)这种半线性或拟线性的抛物方程.
首先, 假设U=U(t,C)为方程Ut=f(U)的通解, 其中C为积分常数; 其次, 设问题(2)的一个解u满足u=U(t,C(t)), 这里C随时间t变化, 此时u对t求导, 得
ut=Ut+UCCt=f(u)+εl(u).

(3)
从方程u=U(t,C(t))中反求C得C=U-1(t,u), 则式(3)可转化为
(4)
该方法称为变异常数的向前Euler法(VCFE), 类似地可推导出变异常数的向后Euler法(VCBE), 这类方法即称为B方法. B方法在求解爆破解和爆破时间时效果较好[12], 本文将B方法用于研究解的猝灭现象.
2 主要结果
2.1 猝灭解的B方法
下面将B方法的思想应用于带有猝灭现象的抛物方程, 其与带有爆破解的方程根本差别在于非线性项不同, 爆破解方程的非线性项一般为指数大于1的增长函数, 而猝灭解方程的指数一般为小于1的函数, 这也决定了具有猝灭解的方程的解随着时间变化会趋向于某一固定值, 但是其解u对于时间的导数却具有爆破现象.
考虑如下方程:
(5)
将B方法应用于方程(5), 由式(3)得
(6)
已知方程解具有猝灭现象的条件[13]为
其中0 2)f=-u-p(p>1). 由g-1=G得 g(u)=C+δt⟹C=g(u)-δt, 以上述结果代入式(6)得 (7) 式(7)可视为由变异常数的向前Euler方法(4)得到的, 简记为VEFE. 式(7)即为B方法在具有猝灭现象抛物方程中的推导应用. 类似地可运用B方法分别写出向后Euler法(VCBE)、 梯形法(VCTR)和中点法(VCMR)的计算格式: 为使G(y)有意义, 其定义域和值域分别为(-∞,1/2]和(-∞,1]. 又由于g和G互为反函数, 易得f与g的定义域为u<1, 其VCFE格式为 证明: 定义Au∶=-Δu, 则式(7)可写成Aun+1=F(x,un+1), 其中 为了应用定理1, 需要证明F(x,0)>0, 即 由例1得f(0)=1,g(0)=0, 且g(un)在满足定义域的条件下大于零, 故F(x,0)>0得证. 下面证明常数Bn是一个上解, 即下列不等式成立: 由猝灭解的定义知, 在方程(1)中函数f(u),g(u)在u=1处存在奇异点, 由例1知0≤u<1, 因此f(un)≥0, 且g(un)是单调递增函数, 往证g(Bn)≥g(un)+δh. 由于G函数此时是单调递增的, 因此Bn≥G(g(un)+δh)>0. 因此, 取常数Bn=G(g(‖un‖∞)+δh)即为一个满足定理1条件的上解, 由定理1知方程组(1)的解存在. 下面用B方法(VCFE)数值研究方程组(1)的猝灭解及猝灭时间的近似模拟, 在方程组(1)中取l=5, 空间剖分步长Δx=0.05. 图1为B方法下计算的数值解u随时间t的变化值, 图2为B方法下计算数值解u对t的导数随时间t的变化值. 由图1和图2可见: 随着时间的增长,u及u对t的导数值也相应增长; 当时间趋近于猝灭时间时, 方程组的解u逐渐趋近于1,u对t的导数趋近于∞. 表明将B方法应用于解具有猝灭解的抛物方程时可以很好地刻画解的猝灭过程. 图1 B方法下方程解u随时间t的变化趋势Fig.1 Variation tendency of solution u with time t of B-method 图2 B方法下解u对t的导数随时间t的变化趋势Fig.2 Variation tendency of derivative of solution u to time t with time of B-method 考虑问题 在满足Dirichlet边值条件下, 初值u0=5×10-5时的解. 在分别取区间长度l=2,π,5,10的条件下, 对区间在空间上均匀剖分, 用Δx表示每个剖分单元长度, 分别取Δx=0.1,0.05,0.02,0.01. 表1列出了不同剖分下向前Euler法和B方法的猝灭时间, 这里根据猝灭时间的定义记u未达到1的最后一个剖分节点对应的时间为猝灭时间. 表1中TE表示运用经典向前Euler法所得到的猝灭时间,TB表示运用B方法得到的猝灭时间. 由表1可见, 运用B方法求得的猝灭时间与经典的向前Euler法求得的猝灭时间几乎相等, 随着剖分单元长度Δx逐渐减小, 猝灭时间也逐渐减小, 与文献[3,10]的数值结果相近, 表明B方法在模拟猝灭时间上具有与经典Euler方法近似的误差, 因而B方法适用于解具有猝灭解的抛物方程. 表1 问题(1)在不同单元长度空间离散下的猝灭时间 [1] Chan C Y, Ke L. Damage Models of Elastic Materials [J]. Dyn Contin Discrete Impul Syst, Ser A: Math Anal, 2001, 8(1): 1-14. [2] Phillips D. Existence of Solutions of Quenching Problem [J]. Appl Anal, 1987, 24(4): 253-264. [3] Sheng Q, Khaliq A Q M. A Compound Adaptive Approach to Degenerate Nonlinear Quenching Problems [J]. Numer Methods Partial Differential Equations, 1999, 15(1): 29-47. [5] Acker A, Walter W. On the Global Existence of Solutions of Parabolic Differential Equations with a Singular Nonlinear Term [J]. Nonlinear Anal, 1978, 2(4): 499-504. [6] Levine H A. Quenching and Beyond: A Survey of Recent Results [J]. GAKUTO Internat Ser Math Sci Appl, 1993, 2: 501-512. [7] GUO Jongsheng, HU Bei. Quenching Problem for a Singular Semilinear Heat Equation [J]. Nonlinear Anal, 1997, 30(2): 905-910. [8] GUO Jongsheng. On the Quenching Behavior of the Solution of a Semilinear Parabolic Equation [J]. J Math Anal Appl, 1990, 151(1): 58-79. [9] Fila M, Levine H A. Quenching on the Boundary [J]. Nonlinear Anal, 1993, 21(10): 795-802. [10] Liang K W, Lin P, Tan R C E. Numerical Solution of Quenching Problems Using Mesh-Dependent Variable Temporal Steps [J]. Appl Numer Math, 2007, 57(5/6/7): 791-800. [11] Sheng Q, Cheng H. An Adaptive Grid Method for Degenerate Semilinear Quenching Problems [J]. Comput Math Appl, 2000, 39(9/10): 57-71. [12] Beck M, Gander M J, Kwok F. B-Methods for the Numerical Solution of Evolution Problems with Blow-Up Solutions Part Ⅰ: Variation of the Constant [J]. SIAM J Comput, 2015, 37(6): A2998-A3029. [13] Nabongo D, Boni T K. Quenching for Semidiscretizations of a Heat Equation with a Singular Boundary Condition [J]. Asymptot Anal, 2008, 59(1/2): 27-38. [14] Amann H. On the Existence of Positive Solutions of Nonlinear Elliptic Boundary Value Problems [J]. Indiana Univ Math J, 1971, 21: 125-146.

2.2 解的存在性
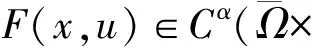

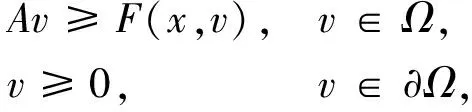

3 数值实验





