一类完全三阶常微分方程边值问题的正解
李嫣红, 李永祥
(西北师范大学 数学与统计学院, 兰州 730070)
1 引言与主要结果
三阶常微分方程边值问题在物理学和应用数学等领域应用广泛[1-2], 如电磁波、 重力流、 三层梁、 地球引力吹积的涨潮以及带有固定或变化横截面弯曲横梁的扰动等均可用三阶常微分方程边值问题描述. 目前, 利用非线性分析的方法求解各类三阶常微分方程边值问题的研究已有很多结果, 如打靶法[2]、 拓扑度法[3]和上下解法[4-5]等. 特别地, 关于其正解的存在性研究也得到广泛关注[6-11]. 对非线性项f不含导数项的简单三阶边值问题(BVP):
(1)
文献[6-9]分别运用Krasnoselskii不动点定理、 锥上的不动点定理、 Leggett-Williams不动点定理、 Leray-Schauder度理论, 得到了BVP(1)正解的存在性; 对非线性项f仅含一阶导数项的三阶边值问题
(2)
文献[10]运用Krasnoselskii不动点定理得到了其正解的存在性.
本文考虑更一般的三阶非线性边值问题:
(3)

为方便, 引入下列假设条件:
(H1) 存在常数a0,a1,a2≥0, 满足a0+a1+a2<1及δ>0, 使得
f(t,x,y,z)≤a0x+a1y+a2z, ∀t∈[0,1], |(x,y,z)|<δ;

f(t,x,y,z)≥b0x+b1y+b2z, ∀t∈[0,1], |(x,y,z)|>H;
(H3) ∀M>0, 存在+上的正连续函数HM, 满足
(4)
使得
f(t,x,y,z)≤HM(|z|), ∀(t,x,y,z)∈[0,1]×[0,M]2×+;
(5)

f(t,x,y,z)≥b0x+b1y+b2z, ∀t∈[0,1], |(x,y,z)|<δ;
(H5) 存在常数a0,a1,a2≥0, 满足a0+a1+a2<1及H>0, 使得
f(t,x,y,z)≤a0x+a1y+a2z, ∀t∈[0,1], |(x,y,z)|>H.
本文主要结果如下:


定理1中, 条件(H1)和(H2)分别允许|(x,y,z)|→0和|(x,y,z)|→+∞时,f(t,x,y,z)关于x,y,z超线性增长, 而条件(H3)限制f(t,x,y,z)关于z的至多二次增长, 是一个关于z的Nagumo型增长条件. 在定理2中, 条件(H4)和(H5)分别允许|(x,y,z)|→0和|(x,y,z)|→+∞时,f(t,x,y,z)关于x,y,z次线性增长.
2 预备知识

构成的Banach空间. 设h∈C(I). 为讨论BVP(3), 先考虑相应的线性边值问题(LBVP):
(6)
引理1对∀h∈C(I), LBVP(6)有唯一解u∶=Sh∈C3(I), 且解算子S:C(I)→C2(I)是线性全连续算子.
证明: 对∀h∈C(I), 易证
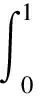
(7)
是LBVP(6)的唯一解. 其中
(8)
为相应的Green函数. 由式(7)易知S:C(I)→C2(I)是线性全连续算子. 证毕.
引理2设h∈C+(I), 则LBVP(6)的解u=Sh有下列性质:
1)u(t)≥0,u′(t)≥0,u″(t)≥0,u‴(t)≤0, ∀t∈I;

证明: 1) 设h∈C+(I),u=Sh为LBVP(6)的解. 由式(7)得
(t,s)h(s)ds,t∈I,
(9)
其中
(10)
由式(9)易得

(11)

u(t)≥0,u′(t)≥0,u″(t)≥0,u‴(t)=-h(t)≤0.
2) 由结论1)知,u(t),u′(t)在I上是非负单调递增函数,u″(t)在I上是非负单调递减函数, 故
(12)
由式(9),(12)知, ∀t∈I, 有

(13)
将式(13)两边从0到t积分, 得
4) 对∀t∈I, 有
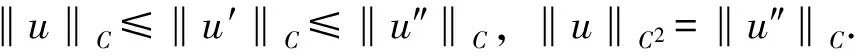
在C2(I)中, 定义闭凸锥K如下:
(14)

F(u(t))∶=f(t,u(t),u′(t),u″(t)),t∈I,
(15)
则F:K→C+(I)连续, 将有界集映为有界集. 定义映射A:K→K如下:
A=S∘F.
(16)
则由S:C+(I)→K的全连续性知,A:K→K是全连续映射. 由S及K的定义知, BVP(3)的正解等价于A的非平凡不动点. 本文应用不动点指数[11-12]的相关结果寻找A的不动点.

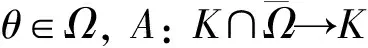


3 主要结果的证明
3.1定理1的证明
取E=C2(I). 设K⊂E是由式(14)定义的闭凸锥,A:K→K是由式(16)定义的全连续算子, 则BVP(3)的正解等价于A的一个非零不动点. 设0 Ω1={u∈C2(I)|‖u‖C2 (17) 取r∈(0,δ), 其中δ>0为条件(H1)中的常数, 下证A满足引理3的条件, 即 μAu≠u,u∈K∩∂Ω1, 0<μ≤1. (18) 假设式(18)不成立, 即∃u0∈K∩∂Ω1, 0<μ0≤1, 使得μ0Au0=u0. 因为u0=S(μ0F(u0)), 由S的定义知,u0是h=μ0F(u0)∈C+(I)对应的LBVP(6)的唯一解. 因此u0∈C3(I)满足方程 (19) (0)≤(a0+a1+a2)‖u0‖C2. (21) i(A,K∩Ω1,K)=1. (22) 取常数 则由假设条件(H2)知,f满足 (23) 定义映射F1:K→C+(I)如下: F1(u(t))∶=f(t,u(t),u′(t),u″(t))+C0=F(u(t))+C0,t∈I. (24) 令A1=S∘F1, 则A1:K→K为全连续算子. 取R>δ,e=S(1). 由引理2知,e=S(1)∈K{θ}. 下证A1满足引理4的条件, 即 u-A1u≠τe,u∈K∩∂Ω2,τ≥0. (25) 假设式(25)不成立, 即∃u1∈K∩∂Ω2,τ1≥0, 使得u1-A1u1=τ1e. 因为u1=S(F1(u1)+τ1), 由S的定义知,u1是h=F1(u1)+τ1∈C+(I)对应的LBVP(6)的唯一解. 故u1∈C3(I)满足方程 (26) 由LBVP(6)解的导数公式(9)与式(12),(23)及引理2中结论3), 得 因此取最大值范数, 有 (27) 下证当R充分大时,A与A1满足引理5的条件, 即 (1-s)Au+sA1u≠u,u∈K∩∂Ω2, 0≤s≤1. (28) 假设式(28)不成立, 则∃u2∈K∩∂Ω2, 0≤s0≤1, 使得(1-s0)Au2+s0A1u2=u2. 因为 u2=S((1-s0)F(u2)+s0F1(u2)), 由S的定义知,u2∈C3(I)是h=(1-s0)F(u2)+s0F1(u2)对应的LBVP(6)的唯一解. 故u2∈C3(I)满足方程 (29) 由LBVP(6)解的导数公式(9)与式(12),(23)及引理2中3), 得 对式(30)两边关于t取最大值, 得 因此 (31) 对此常数M>0, 由假设条件(H3)知, 存在函数HM∈C(+, (0,+∞))满足式(4), 使得式(5)成立. 由式(4)易得因此存在常数M1>M>0, 使得 (32) 于是由方程(29), 得 (33) (34) (35) 由引理2知, 因此由式(31)及式(35), 得 (36) 由式(32),(36)得‖u2‖C2≤M1. 取R>max{M1,δ}. 因为u2∈K∩∂Ω2, 由Ω2的定义知, ‖u2‖C2=R>M1, 与‖u2‖C2≤M1矛盾. 故式(28)成立, 即A与A1满足引理5的条件, 由引理5及i(A1,K∩Ω2,K)=0得 i(A,K∩Ω2,K)=i(A1,K∩Ω2,K)=0. (37) 根据不动点指数的区域可加性及式(22),(37), 有 3.2定理2的证明 设Ω1,Ω2⊂E如式(17)定义,A:K→K为式(16)定义的全连续算子. 由条件(H4), 类似i(A1,K∩Ω2,K)=0的证明, 可证当r充分小时, 有i(A,K∩Ω1,K)=0. 由条件(H5), 类似式(22)的证明, 可证当R充分大时, 有i(A,K∩Ω2,K)=1. 由i(A,K∩Ω1,K)=0和i(A,K∩Ω2,K)=1得 例1考虑超线性三阶边值问题: (38) 因此f(t,x,y,z)满足条件(H2). 由定理1知, 方程(38)至少有一个正解. 例2考虑次线性三阶边值问题: (39) 易证相应的非线性项 满足条件(H4)和(H5). 由定理2知, 方程(39)至少有一个正解. [1] Greguš M. Two Sorts of Boundary-Value Problems of Nonlinear Third Order Differential Equations [J]. Arch Math, 1994, 30(4): 285-292. [2] Troy W C. Solutions of Third-Order Differential Equations Relevant to Draining and Coating Flows [J]. SIAM J Math Anal, 1993, 24(1): 155-171. [3] O’Regan D J. Topological Transversality: Applications to Third Order Boundary Value Problems [J]. SIAM J Math Anal, 1987, 18(3): 630-641. [4] Cabada A. The Method of Lower and Upper Solutions for Second, Third, Fourth and Higher Order Boundary Value Problems [J]. J Math Anal Appl, 1994, 185(2): 302-320. [5] YAO Qingliu, FENG Yuqiang. The Existence of Solution for a Third-Order Two-Point Boundary Value Problem [J]. Appl Math Lett, 2002, 15(2): 227-232. [6] El-Shahed M. Positive Solutions for Nonlinear Singular Third Order Boundary Value Problem [J]. Commun Nonlinear Sci Numer Simul, 2009, 14(2): 424-429. [7] 姚庆六. 三阶常微分方程的某些非线性特征值问题的正解 [J]. 数学物理学报, 2003, 23A(5): 513-519. (YAO Qingliu. Positive Solutions to Some Nonlinear Eigenvalue Problems of Third-Order Ordinary Differential Equations [J]. Acta Mathematica Scientia, 2003, 23A(5): 513-519.) [8] 蒋达清. 三阶非线性微分方程正解的存在性 [J]. 东北师范大学学报(自然科学版), 1996(4): 6-10. (JIANG Daqing. Existence of Positive Solutions for Third-Order Nonlinear Differential Equations [J]. Journal of Northeast Normal University (Natural Science), 1996(4): 6-10.) [9] 徐斌. 非线性三阶边值问题的多解性 [J]. 北京师范大学学报(自然科学版), 2004, 40(4): 448-451. (XU Bin. Multiplicity of Solutions for a Nonlinear Third-Order Boundary Value Problem [J]. Journal of Beijing Normal University (Natural Science), 2004, 40(4): 448-451.) [10] 姚庆六. 一类奇异三阶常微分方程的正解存在性与多解性 [J]. 华东师范大学学报(自然科学版), 2010(3): 113-118. (YAO Qingliu. Existence and Multiplicity of Positive Solutions to a Class of Singular Third-Order Ordinary Differential Equations [J]. Journal of East China Normal University (Natural Science), 2010(3): 113-118.) [11] Deimling K. Nonlinear Functional Analysis [M]. New York: Springer-Verlag, 1985. [12] GUO Dajun, Lakshmikantham V. Nonlinear Problems in Abstract Cones [M]. New York: Academic Press, 1988.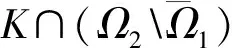


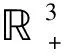



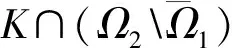
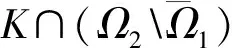
4 应用实例



