高层建筑结构设计中的抗震设计

郑 勇

广东博意建筑设计院有限公司长沙分公司 ，湖南长沙 410000

如今，在城市和经济快速发展的推动下，建筑业面临重大变革，高层建筑逐渐成为主流，在进一步促进城市化进程的同时，也为建筑结构设计，尤其是抗震设计提出了新的要求。因此，有必要对高层建筑的抗震设计给予足够重视，采用合理可行的设计方式，保证设计水平和质量。

1 基于位移的建筑结构抗震设计

1.1 基本参数

1.1.1 位移角限值

设建筑中某层在达到要求的位移角限值时对应的曲线为目标曲线，据此确定最大位移角的具体位置。最大位移角所在位置对框架结构而言，可取柱截面和底层开始发生变化的楼层；对框剪结构而言，可取曲线出现拐点的楼层；而对剪力墙结构，一般直接取顶层。在这种情况下，楼层之间侧向位移，按照楼层的实际位移差值进行计算[1]。

位移的确定需要充分考虑结构性能。为方便分析和计算，现将结构性能分为以下三个等级：一，良好；二，保证人身安全；三，防止倒塌。各等级条件下的位移角限值要求为：（1） 当结构性能为“良好”时，框架结构位移限值应取1/500，框剪结构取1/800，剪力墙结构取1/1000；（2） 当结构性能为“保证人身安全”时，框架结构位移限值应取1/200，框剪结构取1/220，剪力墙结构取1/250；（3）当结构性能为“防止倒塌”时，框架结构位移限值应取1/50，框剪结构取1/100，剪力墙结构取1/120。

1.1.2 结构振型与自振周期

设结构不同振型下的位移形式和它的振型形状相类似，求取不同振型在特定性能下的实际位移目标值，其中应以振型形状的正确选定为前提。就目前来看，高层建筑对应的结构设计，可采用计算机完成，极大地简化了设计和计算的过程，并很好地保证了精度。基于此，本次也采用相应的设计软件实施建模与分析，以获取抗震要求的振型与自振周期。

1.2 目标位移计算

通常将多自由度体系结构转换为等效单自由体系来完成计算和分析，再向多自由度结构施加一定地震作用，以此进行后续结构设计。其中，涉及以下基本假定：首先，体系按照假设的侧向位移出现一定地震反应；其次，转换前后体系有完全一致的基底剪力；最后，转换前后体系所受地震作用相同，即水平方向上由地震力做的功完全一致[2]。

结构的不同阶振型处于弹塑性状态时存在的耦合效率一般可以忽略，通过对非耦合振动作用原理的分析可知，对不同阶振型发生的位移的累计曲线进行组合可以得到结构总位移变化曲线。基于此，即可对各阶振型施以单独分析，同时使上述假定适用于所有振型。

按上述假定进行推导可得：

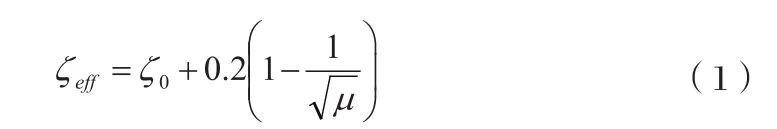
上式中，μ为位移的延性要求，当为弹性阶段时，取1.0；ζ0为弹性阶段时对应的阻尼比，取0.05。可见，若为弹性阶段，则μ为1.0，ζeff和ζ0将相等，即0.05。

1.3 结构不同阶振型的目标侧向位移曲线

非耦合振动作用基本理论、结构位移反应谱、体系转换关系等都为基于高振型的建筑结构侧向位移曲线构建打下了坚实基础。因此，可将不同振型作为依据，采用位移反应谱确定等效位移，再按照等效的基本原理得出位移曲线，最后通过组合得到总体位移。按照结构在弹性和塑性条件下位移曲线相类似的基本假定，找出结构在特定性能情况下的目标位移。据此得到以下计算公式：

上式中，为位移限值；为j阶振型对应的目标位移值；为水平方向上的位移，采用以下公式得出：

1.4 结构地震作用

设结构振型为j，所处楼层为i，则其受到的地震作用可表示为（水平方向）：

设结构振型为j，所处楼层为i，则其受到的地震剪力可表示为：

至此即可完成第一步设计，根据目标位移对结构基底实际剪力与地震作用进行计算分析。根据规范提出的设计模式，可将结构性能为良好的地震作用和自重实施组合，再按照组合后的内力对构建承载力施以准确计算；最后进行标准的延性设计，满足各性能条件下对延性提出的要求。此外，有必要采用静力弹塑性理论，对设计成果进行检验[3]。

2 实例分析

以湖南某拟建高层建筑为例进行分析，设计地上20层（地上1层高4.5m，地上2～20层的高度均为3.3m），上部结构采用框架结构，现浇楼板与框架梁、柱。建筑抗震设防烈度为8度，风荷载取0.45kN/m2，墙体类型采用轻质墙。

根据建筑实际情况，做一下初步设计：（1） 框架柱尺寸地上1、2层为（800×800）mm，地上3～20层为（700×700）mm ；（2）框架梁尺寸横、纵两向分别为（300×700）mm和（300×450）mm；（3） 各层楼板厚度取100mm。建筑结构自重荷载的代表数值与反弯点高度设计计算如表1所示[4]。

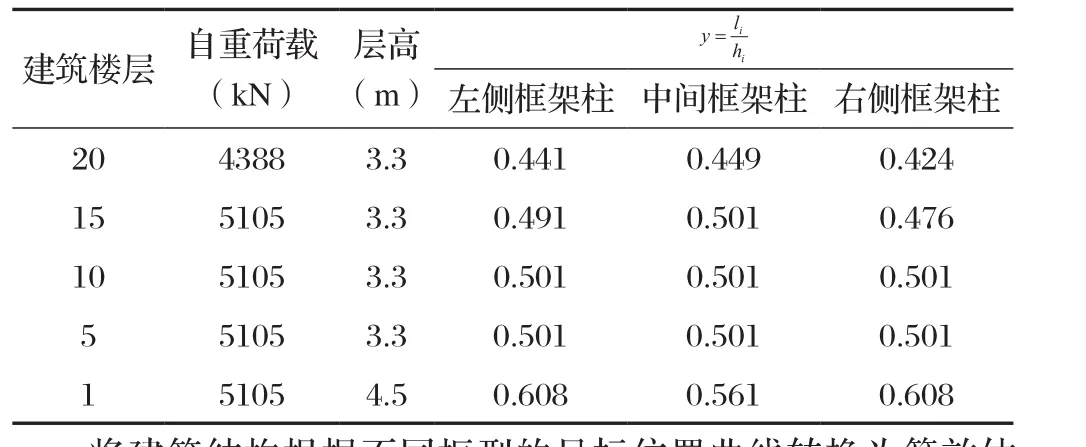
表1 建筑结构自重荷载的代表数值与反弯点高度设计计算

将建筑结构根据不同振型的目标位置曲线转换为等效体系，然后采用以上公式对地震剪力进行计算，再用式 （5） 得出每个楼层的剪力，如表2所示。

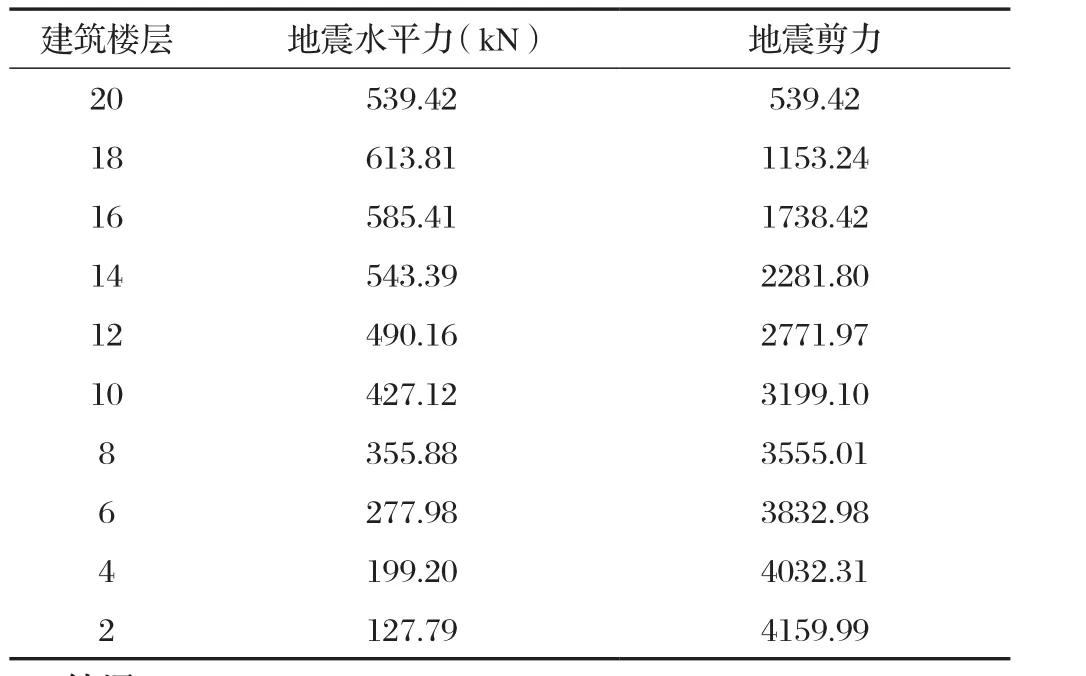
表2 建筑各楼层所受地震力

3 结语

综合上述，基于位移的建筑结构抗震设计合理可行，具有推广应用价值。协调好经济和安全是建筑抗震设计核心内容，抗震设防标准水平在很大程度上决定了社会经济实力。对于高层建筑，其总造价中结构所占比例往往较低，抗震设计方面更是少之又少。因此，在允许的情况下提高标准，并不会增加太大费用，而所能带来的收益却是巨大的。

[1] 李晶晶，颜秉星.高层建筑抗震结构设计探讨[J].智能城市，2017，3（1） ：106.

[2] 高振东.高层建筑抗震设计的几个问题分析[J].黑龙江科技信息，2015（24）：226.

[3] 罗联训.浅论高层混凝土建筑抗震结构设计[J].中华民居（下旬刊），2014（6） ：25.

[4] 靳同良，王多祥.高层建筑抗震设计要点探讨[J].甘肃冶金，2014，36（3） ：140-141，149.