WJ-8型扣件刚度温变规律及其影响研究
周昌盛,盛 曦,周华龙,王 平
(1.中铁二院工程集团有限责任公司地下铁道设计研究院,成都 610031; 2.西南交通大学高速铁路线路工程教育部重点实验室,成都 610031)
无砟轨道因具有整体性强、坚固耐用、轨道变形小、少维修等特点,已在全国范围内得到推广[1-4]。但与此同时,无砟轨道也有弹性差等缺点。为解决上述问题,国内研究人员已开发出了具有优良减振效果的高弹性且刚度可调节的扣件系统。
在大多数扣件中,提供弹性的弹性垫板由黏弹性高分子材料制成,研究资料表明,这类材料的性能受到包括温度在内的多种因素影响[5]。我国幅员辽阔,季节性及区域性温度跨度大,高速铁路线路需穿越各种极端气候区域:哈大线在寒冬穿越气温低至-39.9 ℃的极寒环境,而兰新线在盛夏穿越的戈壁滩气温超过45 ℃,这势必会对扣件的性能发挥带来很大影响。目前,国内外已有文献针对扣件性能温变特性进行了一定研究,并取得了有价值的结论:文献[6]通过设计扣件系统力学性能的模型实验,讨论了宽温域范围内扣件胶垫静/动刚度等力学参数的演变规律;文献[7]以国内地铁扣件中3种不同材料胶垫为研究对象,测取了3类胶垫静刚度在-40~70 ℃范围内随温度的变化规律。然而,仅研究扣件胶垫动力性能随温度的变化规律,并不足以控制温变带来的行车安全隐患。随着我国“高铁走出去”战略的推进,面对世界各地的复杂温度环境,研究扣件胶垫温变性能对行车安全性与平稳性的影响显得迫在眉睫,但经调研,国内此方面的研究却极为缺乏。
鉴于此,基于调研得到的国内各地区温度资料,确定合理的温度范围后进行扣件静刚度温变试验,以国内常用的WJ-8A、WJ-8B型无砟轨道扣件为试验对象,并测取了其刚度随温度的变化情况;在此基础上,建立高速列车-轨道耦合系统动力学模型,分析了不同扣件刚度的温变性对列车行车安全性及平稳性的影响规律。
1 试验概况
1.1 试验原理
通过调节温度箱以模拟现实环境中的温度变化,利用万能试验机测得不同温度点下扣件弹性垫板的力-位移数据,并据相关规范计算胶垫的温变刚度。
1.2 试验条件
(1)测试对象
以我国高速铁路无砟轨道结构中使用较多的WJ-8A及WJ-8B型扣件弹性垫板为研究对象,两种垫板如图1所示。

图1 测试对象
(2)温度点的确定
根据文献[8]中温度统计资料,确定本试验的测试温度区间为-60~70 ℃。另外,根据文献[7]可知黏弹性材料的力学性能具有低温敏感性。因此,试验中在-30~70 ℃区间每隔10 ℃测试1组数据,而在-60~-30 ℃区间每隔5 ℃测试1组数据。
(3)试验设备
①配有温度控制箱的万能试验机
要求万能试验机的加载值为110 kN以上,精度为500 N。温度控制箱能在-70~120 ℃范围内实现无级调节及恒温保持,温度箱与万能试验机配套使用,如图2所示。

图2 配有温度控制箱的万能试验机
②短钢轨
长度大于被测垫板长度的60 kg/m短钢轨。
③加载钢板
弹性垫板加载钢板的长度、宽度与厚度分别为300、170 mm与15 mm。
④支承钢板
弹性垫板支承钢板的长度、宽度与厚度分别为300、170 mm与40 mm。
⑤砂布
粒度为P120(GB/T9258.1《涂附模具用磨料粒度分析第1部分:粒度组成》)的砂布。
⑥传力杆
用于将万能试验机施加的力传递至温度箱内的被测垫板。
⑦位移测试仪
能测定被测弹性垫板表面垂向位移、测量精度±0.01 mm的百分表或其他位移计。
1.3 试验方法
根据相关规范[9]要求完成试验组装后(图3),按照各个温度点数值对温度箱进行调节。在每个温度点上维持1 h(维持1 h后垫板刚度达到稳定)后,首先进行2次100 kN的预加载,然后在位移与荷载调零之后,再以2 kN/s的加载速率,从0 kN逐步加载至70 kN,并分别在加载至20 kN及70 kN时保持1 min,记录该加载过程的荷载(单位:kN)与变形(单位:mm),即弹性垫板的静荷载-位移曲线。

图3 WJ-8型扣件系统弹性垫板刚度的试验组装图
为了获得弹性垫板静刚度,读取弹性垫板的静荷载-位移曲线中20 kN(F1)和70 kN(F2)分别对应的位移D1与D2,然后利用公式(1)计算扣件胶垫的静刚度KSTA。
(1)
1.4 试验结果与分析
遵循以上试验方法,分别测取了WJ-8A、WJ-8B型弹性垫板的静刚度。为了消除试验误差,每个温度点读取了3次数据。
为了直观展示两种弹性垫板的静刚度随温度的变化情况,绘制了静刚度-温度曲线,如图4所示。
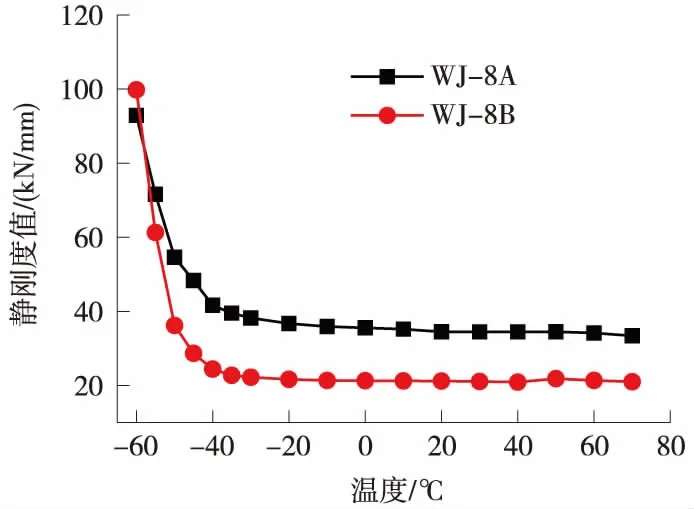
图4 WJ-8型扣件弹性垫板静刚度-温度曲线
从图4可以看出,对于WJ-8A型弹性垫板,温度低于-40 ℃时,其静刚度随着温度的降低而急剧增大;温度在-40~-20 ℃范围内,弹性垫板静刚度随温度的升高缓慢减小;温度高于-20 ℃时,弹性垫板的刚度随温度变化保持较好的稳定性。具体的,与常温(20 ℃)条件下的静刚度值34.5 kN/mm相比,70 ℃时WJ-8A型弹性垫板静刚度为33.4 kN/mm,降幅为3.2%;-40 ℃时静刚度增至41.6 kN/mm,增幅为20.6%;-60 ℃时静刚度进一步增至92.9 kN/mm,增幅高达169.2%。
与WJ-8A型弹性垫板类似,对于WJ-8B型弹性垫板,温度低于-40 ℃时,其静刚度随着温度的降低而急剧增大;温度在-40~-20 ℃范围内,弹性垫板静刚度随温度的升高缓慢减小;温度高于-20 ℃时,弹性垫板的刚度随温度变化保持较好的稳定性。具体的,与常温(20 ℃)条件下的静刚度值21.2 kN/mm相比,70 ℃时WJ-8B型弹性垫板静刚度为21.0 kN/mm,降幅仅为0.98%;-40 ℃时静刚度增至24.4 kN/mm,增幅为15.2%;-60 ℃时静刚度为99.8 kN/mm,增幅高达370.5%。
对比以上两种扣件发现:WJ-8A型扣件及WJ-8B型扣件刚度在温度较高(20~70 ℃)时静刚度值变化不大,而在低温条件下(特别是温度低于-40 ℃时)静刚度随温度降低急剧增大,说明扣件静刚度具有高温稳定性及低温敏感性。
2 轮轨系统动力学模型与计算参数
低温条件下温度对无砟轨道扣件刚度具有显著的影响,而在无砟轨道中,扣件作为轨道结构弹性的主要提供者,其刚度的增大必然会导致轮轨相互作用更加剧烈,引起轮轨系统动力响应的增强,严重的可能影响到上部列车的行车安全性及平稳性。为此,基于轮轨系统动力学理论,建立了高速列车-轨道耦合动力学模型,用于研究扣件温变刚度对轮轨系统动力响应的影响。
2.1 轮轨系统动力学模型
建立高速列车-轨道垂向耦合动力学模型如图5所示,车辆采用全车模型,考虑车体与转向架的沉浮与点头运动,车体与转向架之间由二系弹簧和阻尼器连接,转向架与轮对之间由一系弹簧和阻尼器连接;由于无砟轨道中大部分弹性由扣件系统提供,且本文主要研究扣件刚度变化对轮轨系统影响,因此轨道系统采用单层离散点支承模型,利用有限单元法对其进行离散。
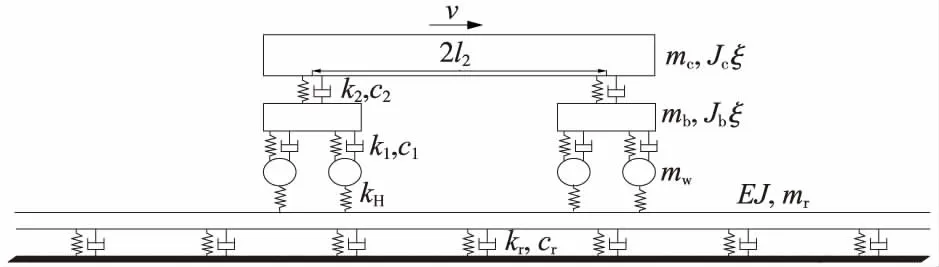
图5 全车-单层弹性点支承轨道平面模型
哈密尔顿原理是分析力学中的一个基本变分原理,它提供了一条从一切可能发生的(约束所许可的)运动中判断真正的(实际发生的)运动的准则,是建立多自由度大型复杂结构系统动力学方程的最有效的基本原理和方法之一[10]。
根据系统的动力平衡原理,可以证明对于任何振动或运动系统,哈密尔顿原理可表达为
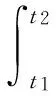
(2)
式中,δ为变分或虚位移符号;t1、t2分别为积分的起始和终止时间;T为系统总动能;U为系统总势能;δW为系统内保守力和非保守力所做的虚功总和。
基于哈密尔顿原理,根据系统的总动能、总势能及相应的虚功,结合计算机中的对号入座法则[11-15],可以方便地建立车辆-轨道系统振动方程组
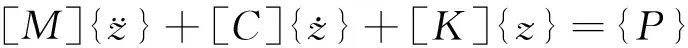
(3)
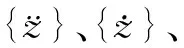
模型建立之后,首先采用Wilson-θ法起步运算,然后再采用Park法求解振动方程组。
2.2 计算参数
计算过程中,行车速度取250 km/h(适用WJ-8A型扣件线路)及350 km/h(适用WJ-8B型扣件线路)两种情况,车辆采用CRH3型高速列车,其结构参数见表1,轨道结构参数见表2。
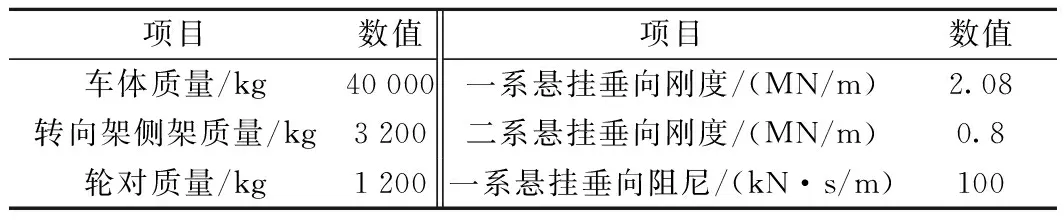
表1 CRH3型高速列车垂向模型参数

表2 轨道结构参数
不平顺轨道谱采用中国高速谱,波长取0.1~200 m,350 km/h速度下随机生成的时域样本如图6所示。
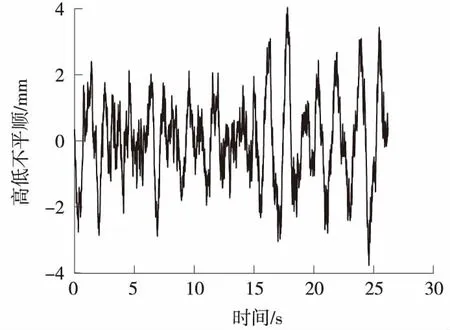
图6 高低不平顺时域样本
3 扣件温变刚度对行车安全性及平稳性的影响研究
结合试验结果与计算模型,仿真模拟各温度下高速列车的实际行车情况,得到相应动力响应。以轮重减载率为安全判定指标,取限值为0.6,分析判断WJ-8A及WJ-8B型无砟轨道线路中扣件温变刚度对行车安全的影响。基于仿真分析得到的车体加速度,以我国车辆研究和制造部门采用的Sperling舒适度指标W为平稳性评判指标,评价分析不同温度条件下各线路列车行车平稳性的优劣。
3.1 扣件温变刚度对行车安全性的影响
基于仿真分析得到的WJ-8A、WJ-8B型扣件支承条件下的轮轨作用力数据,进行后处理分析,得到轮重减载率的时程曲线,其中WJ-8A型扣件条件下结果如图7所示。
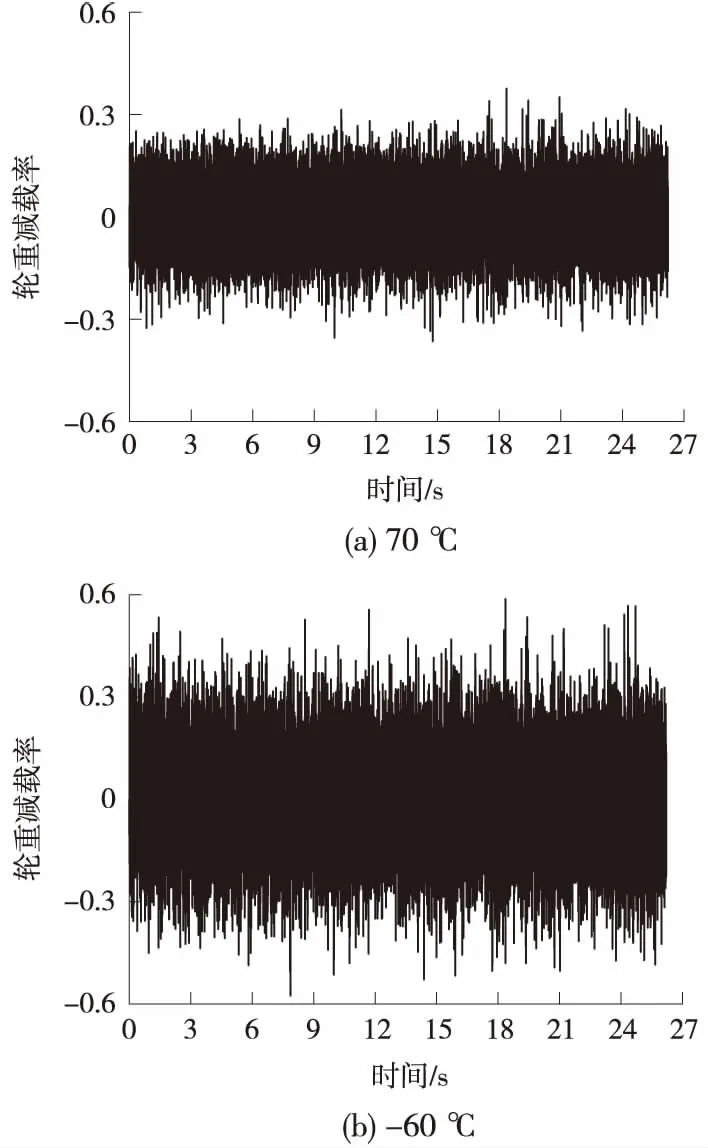
图7 WJ-8A型扣件条件下轮重减载率时程曲线
从图7可以看出,当温度降低时,轮重减载率幅值波动明显变强,轮轨相互作用急剧增大。进一步分析,得到各扣件条件下轮重减载率随温度的变化情况见图8。
由图8可知,两种扣件支承条件下,当温度高于-20 ℃时,轮重减载率随温度变化保持稳定;当温度在-40~20 ℃范围内,轮重减载率随温度的降低而缓慢增大;当温度低于-40 ℃时,轮重减载率随温度的降低而急剧增大,但始终未超过0.6的控制线,说明在温度-60~70 ℃范围内行车安全性能够得到保证。
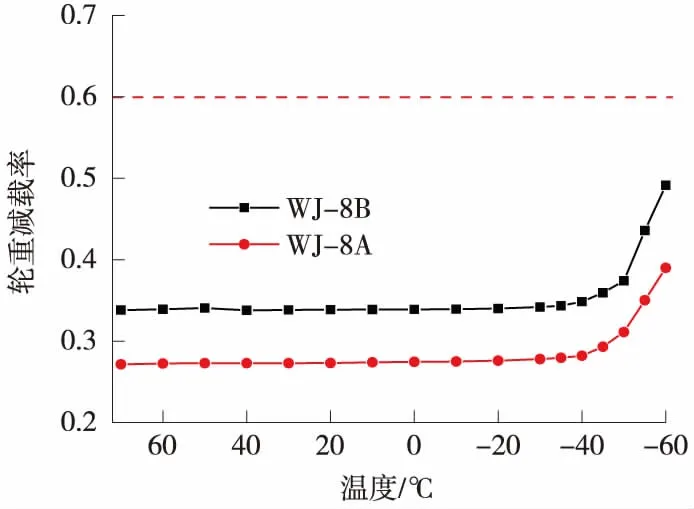
图8 250 km/h线路轮重减载率随温度变化曲线
3.2 扣件温变刚度对行车平稳性的影响
基于仿真分析得到的WJ-8A、WJ-8B型扣件刚度在温变条件下的车体加速度数据,得到车体加速度的时程曲线,其中计算得到的WJ-8A型扣件线路中车体加速度的时程曲线如图9所示。
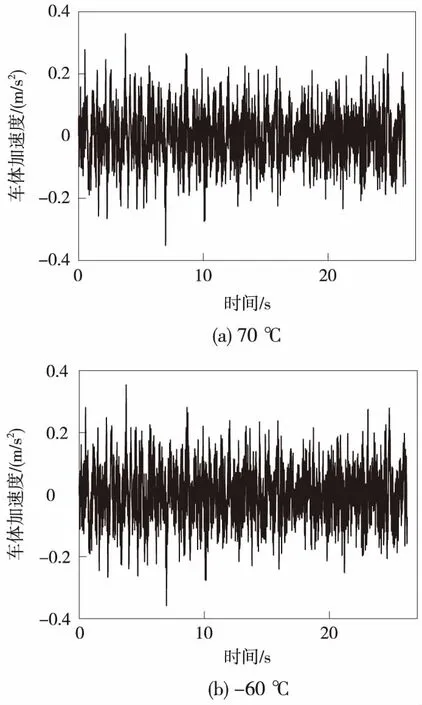
图9 WJ-7A型扣件条件下车体加速度时程曲线
从图9可以看出,温度降低前后车体加速度时程曲线基本一致,说明温度升降引起的扣件刚度变化并未明显影响车体加速度大小。
根据Sperling舒适度指标的计算方法,后处理得到各温度条件下列车平稳性指标,见表3。
分析表3不难发现,无论是WJ-8A型扣件线路,或是WJ-8B型扣件线路,列车以设计速度通过时,其平稳性指标随温度的升降保持稳定。各温度下,列车平稳性指标均保持在1.15(WJ-8A扣件线路)、1.22(WJ-8B扣件线路)附近,未超出规范要求的2.5合格线。
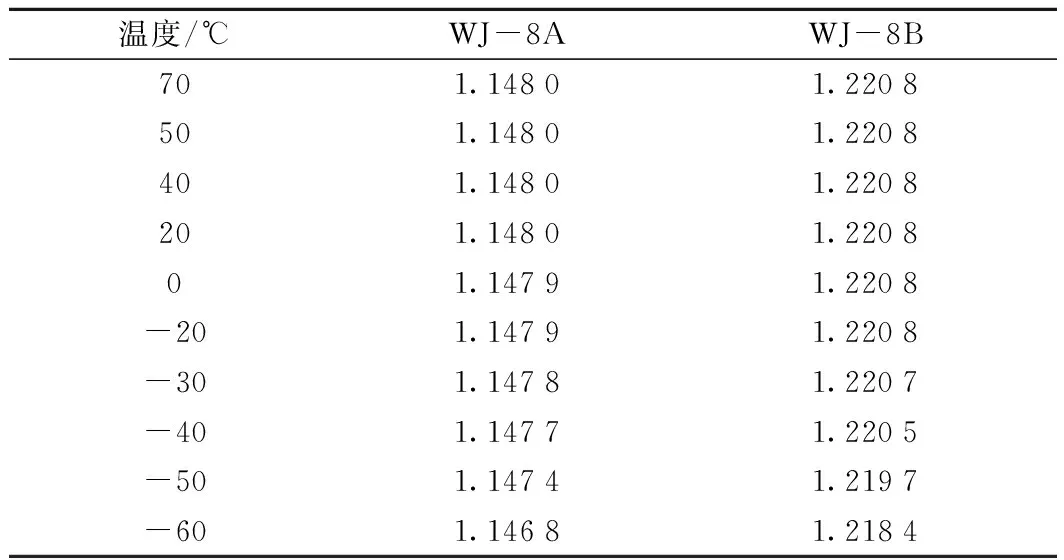
表3 列车平稳性Sperling舒适度指标
4 结论
针对国内无砟轨道线路中使用较多的WJ-8A型、WJ-8B型扣件,采用配备高低温度箱的万能试验机测试系统,进行了-60~70 ℃温度范围内的扣件弹性垫板静刚度测试,研究了温度对于各扣件弹性垫板力学性能的影响规律。其次,结合高速列车-轨道耦合动力学模型及实测的扣件温变刚度数据,以轮重减载率为安全性评价指标,Sperling舒适度指标W为平稳性评判指标,仿真分析了WJ-8A、WJ-8B型扣件温变刚度对线路行车安全性及平稳性的影响,得出以下结论。
(1)无砟轨道扣件在温度高时静刚度值保持稳定,而在低温条件下(特别是温度低于-20 ℃)静刚度急剧增大,说明WJ-8型扣件静刚度均具有高温稳定性及低温敏感性。
(2)在-60~70 ℃温度区间,WJ-8型扣件的温变刚度对列车轮重减载率有影响,温度越低,轮重减载率越大,但计算过程中减载率极值均未超过0.6,列车的行车安全性能够得到保证。
(3)在-60~70 ℃温度区间,WJ-8型扣件的温变刚度对Sperling舒适度指标影响很小,可以忽略,列车平稳性指标均未超过2.5的控制线,列车的行车平稳性能够得到保证;另外,速度对Sperling舒适度指标有影响,速度的增高会使行车平稳性变差。
(4)以上结论是在只考虑扣件刚度温变特性的情况下得出的,而现场情况更加复杂,需进一步深化研究。
(5)本文可为无砟轨道扣件的优化设计提供理论指导,相关仿真计算结果也可为WJ-8A、WJ-8B型扣件在高寒地区的应用可行性提供参考。
[1] 何华武.无砟轨道技术[M].北京:中国铁道出版社,2005.
[2] 朱高明.国内外无砟轨道的研究与应用综述[J].铁道工程学报,2008(7):28-30.
[3] 赵立宁,蔡小培,曲村.地面沉降对路基上单元板式无砟轨道平顺性的影响分析[J].铁道标准设计,2013,57(10):15-18.
[4] 王玉泽,王森荣.高速铁路无砟轨道监测技术[J].铁道标准设计,2015,59(8):1-9.
[5] Miguel S S, Fernando M N,Carmen R G. Viability of Using End-of-life Tire Pads as under Sleeper Pads in Railway[J]. Construction and Building Materials, 2014,64(30):150-156.
[6] I. A. Carrascal, J. A. Casado, J. A. Polanco, et al. Dynamic behavior of railway fastening setting pads[J]. Engineering Failure Analysis, 2007,14(2):364-373.
[7] 韦凯,周昌盛,王平,等.扣件胶垫刚度的温变性对轮轨耦合随机频响特征的影响[J].铁道学报,2016,38(1):111-116.
[8] 中华人民共和国铁道部.TB 10015—2012 铁路无缝线路设计规范[S].北京:中国铁道出版社,2013.
[9] 中华人民共和国铁道部.科技基[2007]207号 WJ-8型扣件暂行技术条件[S].北京:中国铁道出版社,2013.
[10] 刘学毅,王平.车辆-轨道-路基系统动力学[M].成都:西南交通大学出版社,2010.
[11] 赵坪锐.客运专线无砟轨道设计理论与方法研究[D].成都:西南交通大学,2008.
[12] 刘学毅,赵坪锐.客运专线无砟轨道设计理论与方法[M].成都:西南交通大学出版社,2010:161-163.
[13] 张斌,雷晓燕.基于车辆轨道单元的无砟轨道动力特性有限元分析[J].铁道学报,2011,33(7):78-85.
[14] 全顺喜,王平,赵才友.车辆多体系统振动方程建立探讨[J].振动与冲击,2013(11):173-181.
[15] 王平,周昌盛,韦凯,徐浩.随机振动过程中轮轨系统内的能量研究[J].铁道工程学报,2015,37(5):30-41.

