一种使用3D骨架片段表示的人体动作识别方法

刘 沿,姚亚强,陈欢欢

(中国科学技术大学 计算机科学与技术学院,合肥 230027)

1 引 言

人体动作识别是计算机视觉领域最受关注的研究课题之一[1-3],具有广泛的应用领域,包括视频监控,服务机器人和人机交互娱乐等诸多方面.人体动作识别问题实际上是一个分类问题,即根据从训练集中学习到的各种动作特征,找到与测试动作特征最相似的那一类活动,作为测试动作的分类结果.

之前的研究工作专注于从二维视频帧图像中提取图像的局部时空特征[4-6,28,29],比如尺度不变特征(SIFT)[4],方向梯度直方图特征(HOG)和方向光流直方图特征(HOF)[5],以及运动边界直方图特征(MBH)[6].近年来,随着深度摄像机如微软体感摄像机Kinect的出现,同时,Shotton等[7]提供了一种实时地提取人体骨架关节三维坐标位置的方法,两者共同促进了人体动作识别的进一步发展,主要包括基于深度图像[8-11]和基于人体3D骨架信息[12-17]的人体动作识别方法.

通过将人体动作序列坐标通过数学方法转换为李群上的曲线,文献[15]将所得的动作曲线映射为对应的李代数从而达到动作识别的目的.文献[16]根据人体本身的物理结构,将人体骨架划分为五个部分,同时用一种基于端到端的分层的循环神经网络来识别动作.在文献[17]中,为实现更具鲁棒性的识别效果,挖掘具有代表性的称为关键姿势主题的一系列动作视频帧表示对应的动作片段.文献[12,13]与[14]则分别设计了称为3D关节位置统计直方图(HOJ3D)、3D关节位置协方差(Cov3D)和方向位移统计直方图(HOD)的人体动作算子用于动作识别.为表达动作算子序列之间的时间关系,离散隐马尔可夫模型被用于文献[12],而文献[13]和[14]则采用一种平均分割的方法将一个序列分割为长度相等的两段,最终得到一个对人体动作分层的时序的表示.

文献[18]表明,相较于传统的提取的视频图像特征,3D骨架信息在人体动作识别任务中的表现更好,主要原因是相比于视频帧图像特征,3D骨架信息保持了人体姿态的本质信息,且具有观测视角的不变性.基于3D骨架信息所设计的动作算子如3D关节位置统计直方图算子(HOJ3D)[12]、3D关节位置协方差算子(Cov3DJ)[13]以及对应的特征向量)方向位移统计直方图算子(HOD)[14]将该结论应用于人体动作识别领域,取得了令人满意的结果.

本文提出了一种新的使用3D骨架片段表示的人体动作识别方法.图1展示了整个人体动作识别的框架流程图.对于一个人体动作视频,通过Shotton等[7]的方法,可以从每一帧中提取出15(或20)个主要关节的3D坐标位置(x,y,z),这15(或20)个主要关节的坐标位置描述了人体在这一帧中的姿势.对于每一个关节坐标,通过求得其与臀部中心的相对位置,从而保证了姿势的平移不变性.通过这样的处理方式,将一个人体动作表示为一系列的3D骨架坐标(每一帧的3D骨架坐标代表了人体动作在该帧中的具体姿势),其中每一个姿势的坐标点可以看作是高维空间中的点.

本文将人体动作识别问题归结为从训练集中找到与测试样本距离最近的人体动作,从而将测试样本归为该训练动作类别以达到识别未知动作的目标.通过传统的滑动窗口方法,将一个人体动作(一系列的3D骨架坐标)划分为3D骨架片段序列,其中每一个骨架片段都是由一系列连续的高维空间点组成.对于每一个片段,计算该片段包含点的均值及协方差矩阵,其中均值代表了人体动作在这一时间段的主要姿势,而协方差矩阵的前T个特征向量(最大的T个特征值代表了人体动作在这一时间段的主要动作趋势,即片段中动作的进展.主要姿势和主要动作趋势相结合即是对人体动作在该时间段的全面表示.本文同时定义了3D骨架片段与片段之间的距离,该距离的定义结合了主要姿势和主要动作趋势两方面特征.

图1 使用3D骨架片段表示的人体动作识别框架流程图Fig.1 Framework of proposed approach

为了描述人体动作的全局时间关系,用动态时间规整(DTW)算法来度量两个不同动作之间的距离.动态时间规整算法是一个模板匹配算法,其在给定的限制条件下,计算两个给定序列之间(本文中的序列即为3D骨架片段序列)的最优匹配路径及对应的最小成本,该成本即代表了两个序列的匹配程度(距离).本文提出的方法被应用于两个公开发布的人体动作数据集KARD[19]和CAD60[20]上,实验结果表明所提出的使用3D骨架片段表示的方法适用于人体动作识别.

本文主要贡献有以下三个方面:首先,设计出了针对Kinect设备获得的3D骨架信息的使用3D骨架片段表示的人体动作识别框架;其次,对3D骨架片段的表示结合了基于平均值的主要姿势特征和基于主特征向量的主要动作趋势特征,该表示方法具有较强的可解释性;最后,片段之间的距离定义全面地结合了人体动作片段的主要姿势和主要动作趋势两方面特征,使用动态时间规整的模板匹配算法在实验中取得了有竞争力的结果.

2 动作表示

人体骨架可以看作是由刚性杆通过关节链接起来的铰接系统,人体动作则是这个铰接系统的不断变化[21].本文中,将人体动作表示为3D骨架坐标序列.根据文献[7]中实时提取骨架信息的方法,可以得到15(或20)个可接受精度关节点的3D坐标信息:头部、颈部、躯干、左/右肩部、左/右肘部、左/右手、左/右臀部、左/右膝盖、左/右脚、(臀部中心、左/右手腕和左/右脚踝),如图2所示.

图2 人体骨架关节图示Fig.2 Illustration of human skeletons

对于一个人体动作视频,取得其J(15或20)个主要关节的3D坐标位置,其中每个关节的坐标可以表示为:

pj(f)=(xj(f),yj(f),zj(f))

(1)

其中f表示视频帧序数,J个关节的3D坐标位置描述了人体在这一帧中的姿势.对于每一个关节,为了保证姿势的平移不变性,计算其与臀部中心的相对位置:

(2)

其中pc为每一帧中臀部中心的坐标.当J=20时,可直接取得臀部中心的3D坐标;当J=15时,臀部中心的3D坐标为左/右臀部3D坐标的平均.经过这些处理步骤,某一视频帧f中的人体骨架信息可以表示为:

(3)

每一个P(f)代表了人体动作在视频帧f中的姿势.文献[18]表明3D骨架信息在人体动作识别工作中的表现比其它基于视频帧图像特征提取的方法更好,同时,基于姿势序列的动作表示描述了人体动作的固有特征且符合人类自身对动作的学习和认知过程[22],这是本文选择使用3D骨架信息表示人体动作的两个主要原因.

至此,将一个人体动作表示为一系列姿势:

P={P(1),P(2),…,P(f),…,P(F)}

(4)

此处F为动作视频中的总帧数,亦即该动作中包含的总姿势数.每一个姿势P(f)被表示为N维空间中的一个点.

3 动作识别

本文将人体动作识别问题归结为从训练集中找到与测试样本距离最近的人体动作,从而将测试样本归为该训练动作类别以达到识别未知动作的目标.本节首先介绍传统的滑动窗口方法,从而将一个人体动作划分为一系列的3D骨架片段;其次,从每一个3D骨架片段中提取主要姿势和主要动作趋势特征;然后,给出度量两个3D骨架片段之间距离的定义,该定义全面地结合了主要姿势和主要动作趋势特征;最后,介绍动态时间规整算法用来匹配两个动作,从而达到分类的目的.

3.1 滑动窗口划分人体动作序列

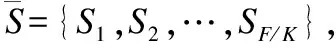
窗口宽度参数K决定了片段的大小和一个动作序列所能划分的片段的个数.较大的K意味着每个片段中包含更多的姿势,对人体动作的描述更加粗糙;相反,较小的K则意味着每个片段中包含更少的姿势,对人体动作的描述更显精确.尽管较小的K对人体动作的描述更加精确,但这意味着更小的片段,其更容易受到3D骨架位置追踪结果噪声的影响,进而影响人体动作的识别效果.本文中探讨了K的大小对人体动作识别结果的影响,从而验证上述推测.

3.2 3D骨架片段特征提取

(5)

该片段内所有姿势的样本协方差矩阵如下:

(6)

Cs是一个N×N的对称矩阵.每一个对称矩阵都是可正交对角化的[23],也就是说,存在一个正交矩阵Q满足:

Q-1CPQ=Λ

(7)

其中Λ是一个对角矩阵,对角线上的元素为实数值,代表了矩阵Cs的N个特征值.主要动作趋势特征T*定义为最大的T个特征值对应的特征向量:

T*=[q1,q2,…,qT]

(8)

qt是一个N维向量代表第t大特征值对应的特征向量.一般而言,对于特定的简单人体动作,实际参与的人体关节数是有限的,甚至在三维空间中的运动方向也是有限的.比如说,动作“画圈”的主要参与人体关节为左手(或右手),在三维空间中的主要运动方向为x和y方向(以垂直于摄像机摄像平面的方向为z轴),因而该动作的运动趋势用左手(或右手)在x和y方向上的变化即可表示.基于上述分析,T*包含最大的T个特征值对应的特征向量,进而描述了动作片段S的主要动作趋势特征.

图3 动作片段主要姿势特征及主要动作趋势特征图示Fig.3 Illustration of major posture feature and main tendency feature of action snippet

图3显示了所定义的动作片段主要姿势特征和主要动作趋势特征,其中T=2.从中可以看出,主要姿势特征代表了人体动作在这一时间段的整体状态,主要动作趋势特征则刻画了人体动作在这一时间段的整体发展方向,两者相结合从而全面地描述了该动作片段.

与此同时,特征向量数T决定了对动作片段主要动作趋势描述的精确程度与鲁棒性.较大的T意味着更多的发展趋势特征,却带来较差的鲁棒性,反之亦然.与前一小节相似,本文中同时探讨了T的大小对人体动作识别结果的影响,从而验证上述推测.

3.3 动作片段间距离度量

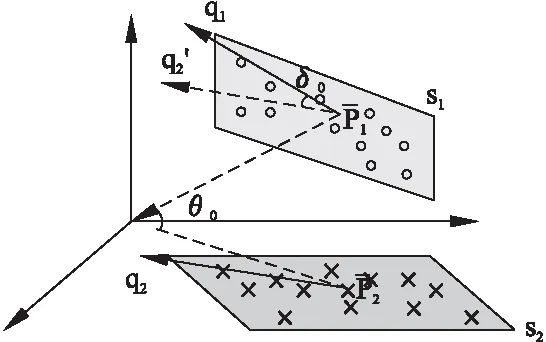
图4 动作片段间距离定义图示Fig.4 Illustration of action snippet-snippet distance

以下分别给出主要姿势距离,主要动作趋势距离的定义,最后将两者结合给出本文提出的动作片段之间的距离定义.

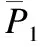
(9)

此处选择正弦距离是为了将其更合理地与主要动作趋势距离相结合,下文中将会涉及.

(10)

类似的,可以定义第二主特征向量正弦距离dT2(S1,S2),第三主特征向量正弦距离dT3(S1,S2)等.本文中,主要动作趋势距离定义为所有主特征向量正弦距离的平均:

(11)

该定义与度量两个子空间距离的方法(主角)基本一致[24],同时考虑到人体动作的特殊性(大部分人体动作仅由人体的部分关节参与),本文中T取1或2.

(12)

3.4 动态时间规整算法匹配

动态时间规整是在给定特定限制条件下计算两个序列间最优匹配及对应距离的模板匹配算法.本文中,给定两个动作序列:训练序列R={R1,R2,…,RM}和测试序列T={T1,T2,…,TN},其中Rm和Tn分别表示训练序列R和测试序列T中的某个动作片段.存在规整路线p={p1,p2,…,pL}从而对齐Rml和Tnl,其中,pl=(ml,nl)代表一个从Rml到Tnl的映射,L是路线长度.两个动作序列之间的距离被定义为具有最小代价的规整路线所对应的距离:

DDTW(R,T)=DTWp*(R,T)

(13)

其中p*是具有最小代价的规整路线,其所对应的距离为:

(14)

其中第一个和第二个限制分别称为边界限制和连续单调限制.动态时间规整算法是通过动态规划实现的,可以有效地找到两个动作序列之间的最佳匹配并计算相对距离.测试动作序列的类别被指派为距离它最近的训练动作序列所对应的类别:

(15)

4 实验结果与分析

为评估本文所提出的人体动作识别方法,将该方法应用于两个公开的人体动作数据集KARD[19]和CAD60[20],每个数据集都提供了人体的15(或20)个关节的3D坐标信息,这些3D关节坐标信息直接应用于人体动作表示.本文中将所提出的方法与其它已公布方法在两个数据集(KARD数据集与CAD60数据集)上的实验结果分别进行比较,并在KARD数据集上进行了相关参数分析.

4.1 KARD数据集

KARD是由Gaglio等人[19]收集的一个人体动作数据,其中包含18种动作,并被划分为10个手势动作(horizontal arm wave,high arm wave,two hand wave,high throw,draw x,draw tick,forward kick,side kick,bend和hand clap)和8个简单活动动作(catch cap,toss paper,take umbrella,walk,phone call,drink,sit down和stand up).每一个动作分别由10个不同对象执行3次,因而总共有540(18×10×3)个视频动作序列.

表1 KARD数据集中的3个动作子集
Table 1 Activity sets grouping different and similar activities from the KARD dataset

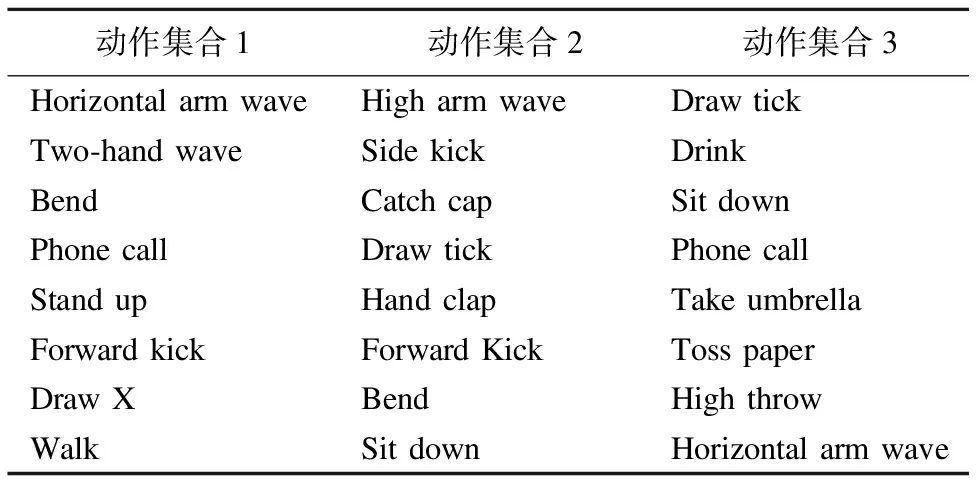
动作集合1动作集合2动作集合3HorizontalarmwaveHigharmwaveDrawtickTwo⁃handwaveSidekickDrinkBendCatchcapSitdownPhonecallDrawtickPhonecallStandupHandclapTakeumbrellaForwardkickForwardKickTosspaperDrawXBendHighthrowWalkSitdownHorizontalarmwave

与文献[19]保持一致,本文中分别考虑三种实验设置和两种动作类别划分方式.其中三种实验设置为:

1)设置A:每个对象的三分之一样本作为训练集,其余的作为测试.

2)设置B:每个对象的三分之二样本作为训练集,其余的作为测试.

3)设置C:所有样本的一半作为训练集,另一半作为测试.

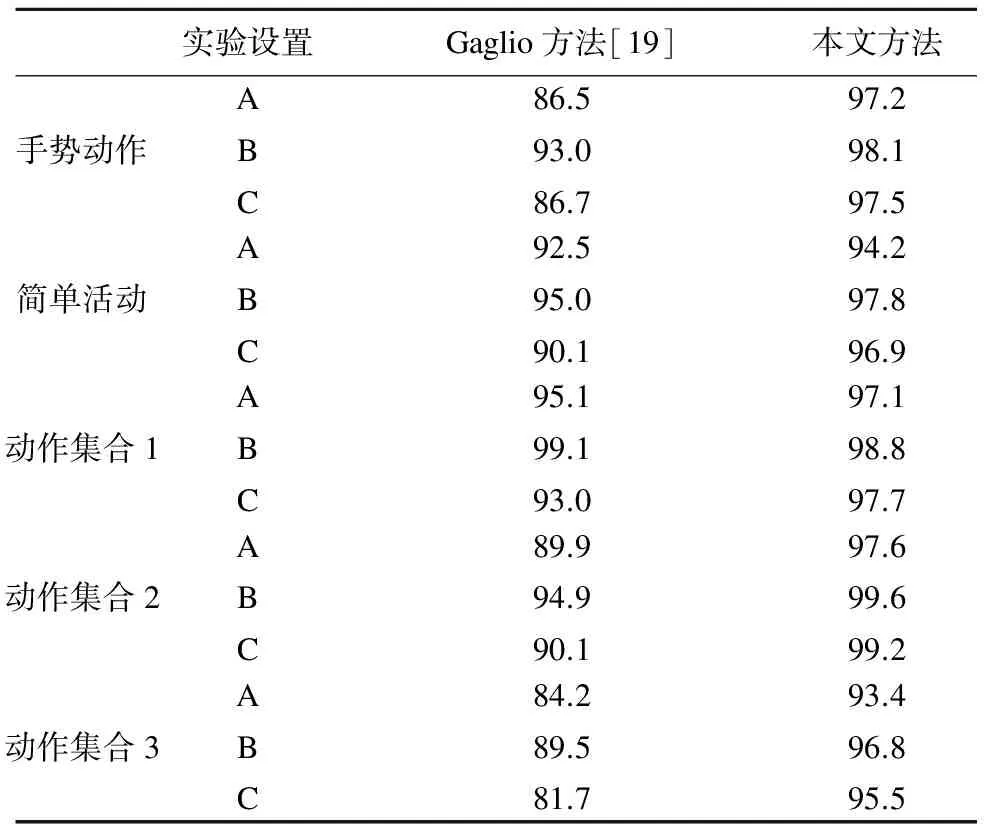
表2 本文方法在KARD数据集上与Gaglio方法[19]识别率的比较(%)
Table 2 Accuracy(%)of the proposed approach compared with the original method[19]using the KARD dataset for different experiment setups with different Activity Sets and split in Gestures/Actions

实验设置Gaglio方法[19]本文方法手势动作ABC86．593．086．797．298．197．5简单活动ABC92．595．090．194．297．896．9动作集合1ABC95．199．193．097．198．897．7动作集合2ABC89．994．990．197．699．699．2动作集合3ABC84．289．581．793．496．895．5

两种动作类别划分方式为:

1)10个手势动作与8个简单活动.

2)动作集合1,动作集合2和动作集合3,如表1所示.其中,动作集合1包含彼此间相似度较低的动作,其它两个动作集合所包含的动作相似度更高.

在KARD数据集上,取滑动窗口宽度参数K=8,主要动作趋势特征中主特征向量数T=1.由于划分原始数据集为训练集和测试集的过程中存在随机性,每个实验设置运行10次并取其平均,实验结果如表2所示.可以看出,本文的方法在几乎所有实验设置中的识别率优于原始方法[19],证明了本文方法的有效性.

同时,本文执行称为“新对象”(leave-one-person-out)的实验设置,即将10个对象中的9个作为训练集,余下的一个作为测试集,该设置与文献[25]保持一致,保证了在测试集中的测试对象不会出现在训练集中,识别结果及与已公布方法的比较如表3所示.本文中使用不同的动作片段间距离度量方法:主要姿势距离、主要动作趋势距离(T=1/2)和定义的动作片段距离(T=1/2,主要姿势与主要动作趋势距离相结合),分别达到的识别准确率为92.5%,93.2%和85.4%,以及96.5%和93.0%,最好结果的识别准确率超出已公布方法的最好结果达1.4%,其它几个结果也达到了较高的识别准确率.

图5显示了对应的混淆矩阵,可以看出,本文方法准确识别了一半以上的动作,但对部分动作之间存在轻微的混淆(如Phone Call与Drink).可以推断,这主要是由3D骨架信息的限制所导致的,添加相对应的图像特征如方向梯度直方图特征(HOG)是一个值得探讨的方法(Phone Call中的电话与Drink中的水杯的图像特征差异较大).总之,从该混淆矩阵中整体上较大的对角线元素可以看出,本文方法在该数据集上有较高的识别准确率.

表3 本文方法在KARD数据集上的识别率(%)与已公布方法的比较,采用“新对象”实验设置
Table 3 Accuracy(%)of the proposed approach compared with the state-of-the-art approaches,using the KARD dataset under “leave-one-person-out” setting

方 法识别率%公布方法Gaglio方法[19]2015Cippitelli方法[25]201684．895．1本文方法主要动作趋势距离(T=2)主要姿势距离动作片段距离(T=2)主要动作趋势距离(T=1)动作片段距离(T=1)85．492．593．093．296．5

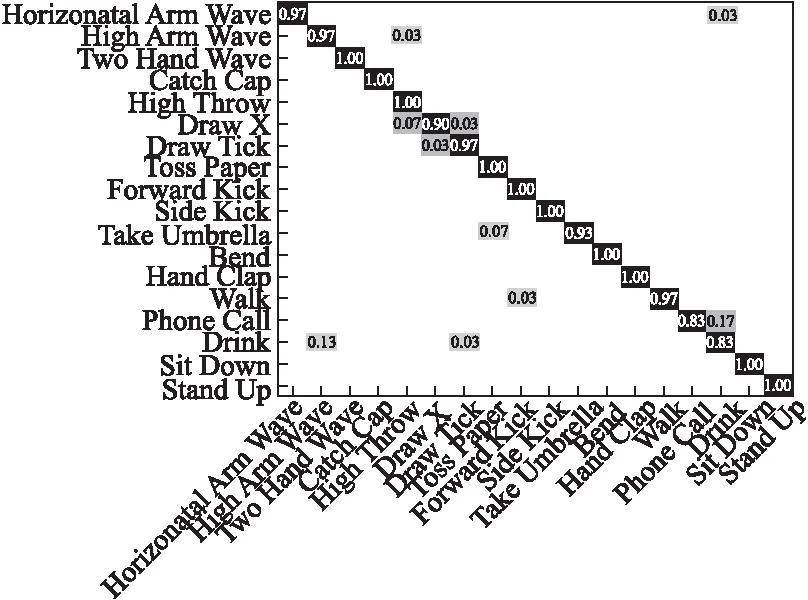
图5 本文方法在KARD数据集上采用“新对象”实验设置的混淆矩阵Fig.5 Confusion matrix of the proposed approach on the KARD dataset using “leave-one-person-out” setting

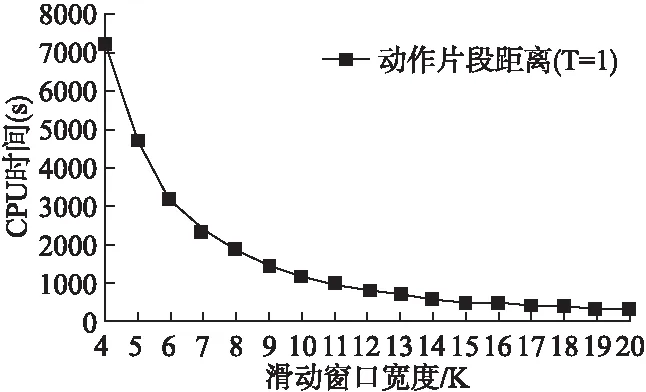
图6 本文方法在KARD数据集上采用“新对象”实验设置的CPU时间比较图Fig.6 CPU time comparison of the proposed approach on the KARD dataset using “leave-one-person-out” setting

算法运行时间比较分析:文献[19]中在CPU为2.6-GHz Dual Core的台式电脑上运行MATLAB实现了一个实时人体动作识别系统.本文所有实验同样使用MATLAB运行于CPU为3.4-GHz Dual Core的台式电脑,如图6所示,横坐标为滑动窗口宽度K,纵坐标为对应的CPU时间(KARD上所有540个人体动作采用“新对象”实验设置的CPU时间),K以间隔1从4取到20.实际上,本文方法的时间复杂度与F/K近似成正比(主要由动态时间规整算法决定,复杂度为O(M+N),其中M和N分别为两个序列的长度,与F/K相关),即与K成反比,图6中近似反曲线去我们的分析相一致.此外,本文的方法同样实现了实时性,以K=8为例,540个人体动作的CPU时间约为1844s,则每一个人体动作的CPU时间3.4s,小于人体动作视频的平均长度(4.9s),因而,本文方法在基本配置条件下依然实现了一个实时的人体动作识别系统.

本文方法参数分析:这部分评估不同的参数组合(滑动窗口宽度K、主要动作趋势特征中主特征向量数T)及不同的动作片段距离度量方式对动作识别性能的影响.在图7中,横坐标为滑动窗口宽度K,纵坐标为对应的识别率,K以间隔1从4取到20.对比识别率曲线“动作片段距离(T=1)”与“动作片段距离(T=2)”,可以看出“T=1”的识别率始终高于“T=2”,这是因为第一主特征向量已具有较强的区分能力,第二主特征向量则相互间有混淆,在计算主要动作趋势距离时给予两者相同的权重导致了识别率的下降,也就是说,在该数据集上,主要动作趋势特征中主特征向量数T取值1是一个基于准确率的最佳选择.对比识别率曲线“主要姿势距离”与“主要动作趋势距离(T=1)”,可以看出,K较小时,“主要姿势距离”的识别率优于“主要动作趋势距离(T=1)”,而随着K的增长,“主要姿势距离”的识别率逐渐下降,而“主要动作趋势距离(T=1)”的识别率基本保持平稳,即K较大时,“主要姿势距离”的识别率差于“主要动作趋势距离(T=1)”.该现象的可以归结为随着K的增大,“主要姿势特征”已不能够精确表达动作片段的特征,导致“主要姿势距离”的区分度下降,而“主要动作趋势特征”具有描述更大片段中动作趋势的能力,因而“主要动作趋势距离”的识别率并不随K的增大而下降,其描述动作趋势的能力弥补了大片段精确度表达不足的问题,因而识别率保持平稳.总体而言,“动作片段距离(T=1)”结合了“主要姿势距离”和“主要动作趋势距离(T=1)”两方面的优势,在几乎所有的参数条件下达到了最高的识别率,并随滑动窗口宽度K的变化保持平稳,这是本文提出该动作片段距离度量方法的主要原因.

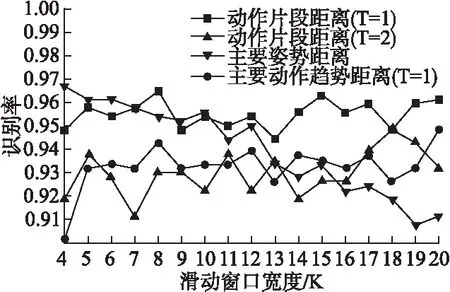
图7 本文方法在KARD数据集上采用“新对象”实验设置的不同参数比较图Fig.7 Parameter comparison of the proposed approach on the KARD dataset using “leave-one-person-out” setting

4.2 CAD60数据集

CAD60[20]数据集英文全称为Cornell Activity Dataset,其中包含12个独立的动作:rising mouth with water,brushing teeth,wearing contact lens,talking on the phone,drinking water,opening pill container,cooking(chopping),cooking(stirring),talking on couch,relaxing on couch,writing on whiteboard,working on computer.四个不同的对象(其中一个为左撇子,两位男性,两位女性)在五种不同的环境(浴室、卧室、厨房、客厅和办公室)中执行以上活动,每种环境包括三到四种动作.

表4 本文方法在CAD60数据集上的识别率(%)与已公布方法的比较
Table 4 Accuracy(%)of the proposed approach compared with the state-of-the-art approaches,using the CAD60 dataset under “leave-one-person-out” setting

方 法识别率%Wang方法[10]201474．7Koppula方法[26]201380．8Hu方法[27]201584．1Cippitelli[25]方法201693．9本文方法(K=10，T=1)98．5

与文献[10]所采用的实验设置保持一致,即对于每一种环境,执行被称为“新对象”(leave-one-person-out)的实验设置,这意味着测试对象不会出现在训练集中.由于四个人中的一个是左撇子,实验中当左手的y坐标大于右手时,交换两者的y坐标以及与之关联的左右肘关节、肩关节的y坐标,通过该方法实现了左撇子与其它三人操作的统一.取K=10且T=1时,采用本文所定义的“动作片段距离”,将所有20(5×4)可能的划分分别进行实验,所得识别率与已公布方法的比较如表4所示,本文方法的识别率达到98.5%,较之已公布的方法有了大幅度的提升(最好的为93.9%).

5 结 论

本文针对Kinect获得的3D骨架数据,提出了一种新的使用3D骨架片段表示的人体动作识别方法.提出的动作片段的表示结合了均值所代表的主要姿势特征和主特征向量所代表的主要动作趋势特征,并对两者的表示能力进行了实验分析.运用动态时间规整算法匹配动作片段序列从而达到动作识别的目的,在两个公开数据集KARD和CAD60的实验结果表明本文提出的方法具有较高的识别率和较强的普适性.在未来的工作中,考虑结合图像特征信息从而摆脱3D骨架数据的限制性,以期达到更佳的识别能力.

[1] Aggarwal J K,Ryoo M S.Human activity analysis:a review[J].ACM Computing Surveys(CSUR),2011,43(3):16：1-16：43.

[2] Aggarwal J K,Xia L.Human activity recognition from 3d data:a review[J].Pattern Recognition Letters,2014,48(1):70-80.

[3] Vrigkas M,Nikou C,Kakadiaris I A.A review of human activity recognition methods[J].Frontiers in Robotics and AI,2015,2(1):1-28.

[4] Lowe D G.Distinctive image features from scale-invariant keypoints[J].International Journal of Computer Vision(IJCV),2004,60(2):91-110.

[5] Laptev I,Marszalek M,Schmid C,et al.Learning reslistic human actions from movies[C].IEEE Conference on Computer Vision and Pattern Recognition(CVPR),2008:1-8.

[6] Wang H,Kläser A,Schmid C,et al.Dense trajectories and motion boundary descriptors for action recognition[J].International Journal of Computer Vision(IJCV),2013,103(1):60-79.

[7] Shotton J,Sharp T,Kipman A,et al.Real-time human pose recognition in parts from single depth images[J].Communications of the ACM,2013,56(1):116-124.

[8] Oreigej O,Liu Z.Hon4d:histogram of oriented 4d normals for activity recognition from depth sequences[C].IEEE Conference on Computer Vision and Pattern Recognition(CVPR),2013:716-723.

[9] Xia L,Aggarwal J K.Spatio-temporal depth cuboid similarity feature for activity recognition using depth camera[C].IEEE Conference on Computer Vision and Pattern Recognition(CVPR),2013:2834-2841.

[10] Wang J,Liu Z,Wu Y,et al.Learning actionlet ensemble for 3d human action recognition[J].IEEE Transactions on Pattern Analysis and Machine Intelligence(TPAMI),2014,36(5):914-927.

[11] Rahmani H,Mahmood A,Huynh D,et al.Histogram of oriented principal components for cross-view action recognition[J].IEEE Transactions on Pattern Analysis and Machine Intelligence(TPAMI),2016,38(12):2430-2443.

[12] Xia L,Chen C C,Aggarwal J K.View invariant human action recognition using histograms of 3d joints[C].IEEE Conference on Computer Vision and Pattern Recognition Workshops(CVPRW),2012:20-27.

[13] Hussein M E,Torki M,Gowayyed M A,et al.Human action recognition using a temporal hierarchy of covariance descriptors on 3d joints locations[C].International Joint Conference on Artificial Intelligence(IJCAI),2013:2466-2472.

[14] Gowayyed M A,Torki M,Hussein M E,et al.Histogram of oriented displacement(hod):describing trajectories of human joints for action recognition[C].International Joint Conference on Artificial Intelligence(IJCAI),2013:1351-1357.

[15] Vemulapalli R,Arrate F,Chellappa R.Human action recognition by representing 3d skeletons as points in a lie group[C].IEEE Conference on Computer Vision and Pattern Recognition(CVPR),2014:588-595.

[16] Du Y,Wang W,Wang L.Hierarchical recurrent neural network for skeleton based action recognition[C].IEEE Conference on Computer Vision and Pattern Recognition(CVPR),2015:1110-1118.

[17] Wang C,Wang Y,Yuille A L.Mining 3d key-pose-motifs for action recognition[C].IEEE Conference on Computer Vision and Pattern Recognition(CVPR),2016:2639-2647.

[18] Yao A,Gall J,Fanelli F,et al.Does human action recognition benefit from pose estimation[C].British Machine Vision Conference(BMVC),2011:67.1-67.11.

[19] Gaglio S,Re G L,Morana M.Human activity recognition process using 3-d posture data[J].IEEE Transactions on Human-Machine Systems(THMS),2015,45(5):586-597.

[20] Sung J,Phonce C,Selman B,et al.Unstructured human activity detection from rgbd images[C].IEEE International Conference on Robotics and Automation(ICRA),2012:842-849.

[21] Zarsiorsky V M.Kinects of human motion[M].Human Kinects,2002.

[22] Bülthoff I,Bülthoff H,Sinha P.Top-down influences on stereoscopic depth-perception[J].Nature Neuroscience,1998,1(3):254-257.

[23] Lang S.Introduction to linear algebra[M].Springer Science & Business Media,2012.

[24] Björck A,Golub G H.Numerical methods for computing angles between linear subspaces[J].Mathematics of Computation,1973,27(123):579-594.

[25] Cippitelli E,Gasparrini S,Gambi E,et al.A human activity recognition system using skeleton data from rgbd sensors[J].Computational Intelligence and Neuroscience,2016,10(1):1-15.

[26] Koppula H S,Gupta R,Saxena A.Learning human activities and object affordances from rgb-d videos[J].International Journal of Robotics Research(IJRR),2013,32(8):951-970.

[27] Hu J,Zheng W S,Lai J,et al.Jointly learning heterogeneous features for rgb-d activity recognition[C].IEEE Conference on Computer Vision and Pattern Recognition(CVPR),2015:5344-5352.

[28] Liu Chang-hong,Yang Yang,Liu Ying-hui.Spatio-temporal pyramid matching using sparse coding for action recognition[J].Journal of Chinese Computer Systems(JCCS),2012,33(1):169-172.

[29] Feng Ming,Chen Jun.Efficient action recognition based on local binary descriptor[J].Journal of Chinese Computer Systems(JCCS),2016,37(6):1289-1292.

附中文参考文献：

[28] 刘长红,杨 杨,刘应辉.基于稀疏编码的时空金字塔匹配的动作识别[J].小型微型计算机系统,2012,33(1):169-172.

[29] 冯 铭,陈 军.基于局部二进制描述符的高效动作识别方法[J].小型微型计算机系统,2016,37(6):1289-1292.