置信优势关系粗糙集的属性约简方法

苟光磊,王国胤

1(重庆理工大学 计算机科学与工程学院,重庆 400054) 2(重庆邮电大学 计算智能重庆市重点实验室,重庆 400065)

1 引 言

优势关系粗糙集模型(Dominance-based Rough Set Approach,DRSA)[1,2]常被用于处理序信息系统的决策问题.与经典粗糙集[3]基于等价关系不同,DRSA基于优势关系,其条件属性及决策属性具有偏好有序的特性.实际应用环境中,由于数据采集技术的限制、传输故障等因素造成数据缺损和丢失,形成不完备有序信息.然而,DRSA无法处理不完备有序信息,因而,通过拓展优势关系,置信优势关系粗糙集[4]被提出用于处理不完备有序决策系统(Incomplete Ordered Decision System,IODS).

属性约简是粗糙集理论及其扩展模型研究的核心问题之一[5,6].在完备有序信息系统中,多种约简方法被提出.其中,Dembczyński[1]等给出了基于分类精度的约简概念,却没有提出相应的约简方法.徐伟华等提出了多种基于DRSA的约简方法,包括分布约简和最大分布约简[7],可能分布约简(分配约简)及相容分布约简[8].Inuiguchi等提出了基于决策属性联合类的上、下近似、边界域不变的约简方法[9],Kusunoki进一步给出决策属性基于类的上、下近似、边界域不变的约简方法[10].Susmaga提出了经典粗糙集和优势关系粗糙集的约简的统一定义框架和构造方法[11].Gou等提出基于优势原理的属性约简方法[12].Chen等提出了基于优势的领域粗糙集并行属性约简方法[13].

上述有序信息系统的约简方法在不完备情况下不再适用.为得到不完备有序信息系统的约简,Shao等提出基于扩展优势关系粗糙集模型的约简方法[14]用于处理不协调不完备有序决策系统.Yang等提出相似优势关系粗糙集模型处理不完备有序决策系统,进一步给出保持上、下近似分布约简方法[15].Yang等讨论了不完备区间值信息系统中的多种相对约简方法[16].苟光磊等讨论了不协调置信优势原理关系的属性约简方法[17].以上多种方法都是基于辨识矩阵的,可获得所有的约简,但约简过程耗时,效率低.

1Lichman, M. UCI Machine Learning Repository[OL] http://archive.ics.uci.edu/ml. 2013.

本文将讨论基于置信优势关系粗糙集的约简方法,首先讨论了在属性域上,分类精度呈现单调性;然后给出核属性概念,提出置信优势关系粗糙集基于分类精度的启发式属性约简方法;由于启发式约简方法中,每次增加或删除一个属性,都会重新计算整个上、下近似集而得到分类精度,为此,讨论了增加或删除一个属性后,上、下近似集的变化情况,从而改进启发式约简方法,提出增量式属性约简方法.最后,在UCI1数据集上的实验结果表明,增量式约简方法相对于启发式约简方法,时间效率更高.

2 置信优势关系粗糙集

假设决策系统DS=(U,A,V,f),U表示论域,A是属性集合,A=C∪D,其中C和D分别表示条件属性集合决策属性集.V是属性值域,具有偏好.f:U×A→V是信息函数.f(xi,a)表示对象xi在属性a上的取值.如果所有的属性值都已知,则称为完备有序决策系统.如果存在缺失值,则称为不完备有序决策系统(Incomplete Ordered Decision System,IODS).缺失值用 “*”表示.

设a∈A具有偏好有序关系,记为a.xay,x,y∈U表示在属性a上对象x至少和y一样好.增序偏好下,xay表示f(x,a)≥f(y,a),降序偏好下,则表示f(x,a)≤f(y,a).为便于讨论,在不作特别说明的情况下,本文将采用增序偏好.

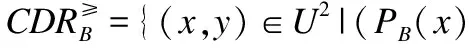
(∀q∈P(f(x,q)≠*)→(f(y,q)f(x,q)))}

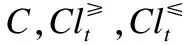
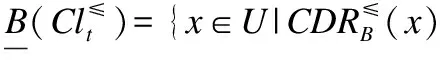
边界域的表示如下:

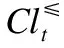
定义3.[4]分类精度定义如下

3 基于分类精度的启发式约简方法

不完备有序决策系统中,置信优势关系粗糙集具有如下性质.

性质1.假设IODS=(U,A,V,f),其中A=C∪D,Cl={Clt|t∈{1,2…,n}}.

3)γB(Cl≥)=γB(Cl≤)

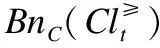
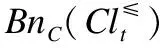
5)B⊆C⟺γB(Cl≥)≤γC(Cl≥),γB(Cl≤)≤γC(Cl≤)

证明:

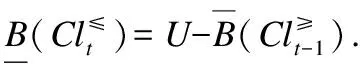
3)由性质1(2)轻松得到.

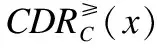
5)由性质1(4)轻松得到.

由性质1可以发现,基于置信优势关系粗糙集的分类精度在属性域上呈现单调性,随着条件属性的增加,分类精度也随之增加.

定义4.属性重要性 设不完备有序决策系统IODS=(U,A,V,f),A=C∪D,B⊆C,其中a⊆C-B,属性a的重要性表示为:

sig(a,B)=γB(Cl≥)-γB/{a}(Cl≥).

显然,0≤sig(a,B)≤1.如果sig(a,B)=0,该属性a对于属性集合B而言是冗余的,否则,a就是属性集合B中的核属性.

定义5.设不完备有序决策系统IODS=(U,A,V,f),若γB(Cl≥)=γC(Cl≥),且B的任何真子集B′,满足γB′(Cl≥)=γC(Cl≥),称B是IODS的约简.

因此,根据置信优势关系粗糙集分类精度在属性域上的单调性以及属性重要性,提出保持分类精度不变的启发式属性约简方法,见算法1.

算法1.基于分类精度的启发式属性约简

输入:不完备有序决策表IODS=(U,A,V,f)

输出:属性约简red

1.red=∅,core=∅

2. 计算分类精度γC(Cl≥);

3.foreacha∈C

4.ifγC-{a}≠γC

5.core=core∪{a};

6.endif

7.endfor

8.A=C-core;red=core;

9.whileγC≠γred

10. 计算属性重要性sig(i)=γcore∪{a}(Cl≥)-γcore(Cl≥);

11. 选择属性a∈C得到最大的sig;

12.red=red∪{a};A=A-{a};

13.endwhile

14. 根据属性重要性对red里的属性进行降序排序

15.whilered≠φ

16.ifγred-{a}=γC

17.red=red-{a}

18.endif

19.endwhile

算法1的3-6步目标是从条件属性集C中找出核属性,若核属性集能够保持系统的分类精度,则核属性即为约简结果.若核属性集不能保持系统的分类精度或者不存在核属性,算法1的9-13步则从冗余属性中按照属性重要性的高低加入到核属性,直到满足分类精度不变为止,算法1的15-19则对满足分类精度不变的约简结果再次精简.

4 基于分类精度的增量式属性约简方法

上一节,提出基于分类精度的启发式属性约简方法.从算法1可以看出每次在增加一个属性或者删除一个属性时,都会重新计算整个近似域来获得分类精度,为此,本节讨论单个属性变化时,近似集的动态变化规律,给出分类精度的增量式算法,提出基于分类精度的增量式约简方法,改进约简效率.

定义6.假定IODS=(U,A,V,f),对任意的x∈U,有

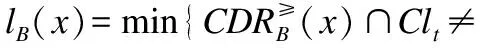
引理1.假定IODS=(U,A,V,f),B⊂C,a∈C-B,增加属性时,置信优势集、置信劣势集的变化满足

证明:

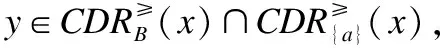
2)同理可证.

引理2.假定B⊆C,a∈B,属性减少时,置信优势集、置信劣势集的变化满足

“：”表示非.

证明:

2)同理可证.

定理1.假定B⊆C,a∈B,属性增加时,上、下近似变化

证明:

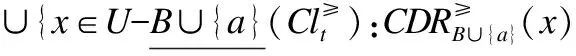
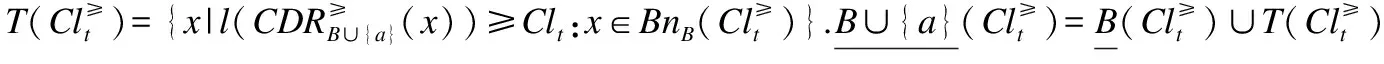
定理2.假定B⊆C,a∈B,属性减少时,上、下近似变化

证明:

根据定理1-2,在增加或删除单个属性时,得到置信优势关系粗糙集的上、下近似集的变化规律,可给出分类精度的增量式算法见算法2与算法3.

算法2.删除单个属性后的分类精度

输出:γB-{ai}

1.foreacha∈C

4.end

5.fori=1:n

10.end

算法3.增加单个属性后的分类精度

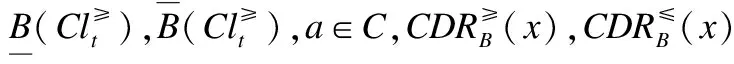
输出:γB∪{a}

1.fori=1:|U|

3.end

4.fori=1:n

9.end

在条件属性集B中删除单个条件属性或增加单个条件属性时,算法2,3利用已知的条件属性集B的上、下近似等知识,增量式更新分类精度,无需重新计算整个论域.

我们使用算法2替换算法1中的4,16行,用算法3替换算法1中的10行,利用增量式方式更新论域的上、下近似得到分类精度,得到基于分类精度的增量式约简方法,见算法4.

算法4.基于分类精度的增量式属性约简

输入:不完备有序决策表IODS=(U,A,V,f)

输出:属性约简red

1.red=∅,core=∅

2. 计算分类精度γC(Cl≥);

3. for eacha∈C

4.if算法2计算γC-{a}≠γC

5.core=core∪{a};

6.endif

7.endfor

8.A=C-core;red=core;

9.whileγC≠γred

10.算法3计算γcore∪{a}(Cl≥)

11. 计算属性重要性sig(i)=γcore∪{a}(Cl≥)-γcore(Cl≥);

12. 选择属性a∈C得到最大的sig;

13.red=red∪{a};A=A-{a};

14.endwhile

15. 根据属性重要性对red里的属性进行降序排序

16.whilered≠∅

17.if算法2计算γred-{a}=γC

18.red=red-{a}

19.endif

endwhile

5 仿真实验

我们将通过仿真实验来验证上述方法的正确性和有效性.为此,我们在UCI的五个数据集(见表1)进行了实验,除了car为完备数据集外,其余均为不完备数据集,完备数据集可视为不完备数据集的特例.实验环境为Lenovo X220i配置为Intel i3-2370 2.4GHz,内存4GB,Windows 7(32bit),使用Matlab R2012b编程实现.

表1 数据集描述
Table 1 Description of data sets

ID数 据 集|U||C|1Hepatitis155192Ionosphere351343breast-cancer699104mammographic-masses96155car17266

实验将基于分类精度的启发式约简方法(算法1)与基于分类精度的增量式约简方法(算法4)进行比较.实验结果如表2,两种约简方法得到的约简是一致的.当论域对象个数较少时,增量式方法并不优于启发式约简方法即算法1,如Hepatitis数据集.当随着论域对象个数增加时,增量式属性约简算法的效率也逐步优于非增量式的约简算法.

表2 启发式算法与增量式方法运行时间对比/s

Table 2 A comparison of running time between incremental and non-incremental(s)

ID算法1算法4约简后的属性12．2192553．0408582，4，5，6，10，11，15，16，17，18，19248．4789147．05986，8，10，14，17，24，29323．269720．841731，2，4，5，6，7，8，9，10426．387521．853981，2，3，4，5585．2206474．551854，6

接着,我们选用了NaiveBayes、ClassificationTree以及置信优势关系粗糙集分类精度来对比约简前后的分类正确率,实验结果见下页表3,属性约简前后,置信优势关系粗糙集的分类精度保持不变.从NaiveBayes、ClassificationTree分类器的正确率可以看出,在完备数据集car上,属性约简后的分类正确率有所降低.然而,在不完备的数据集中,约简前后的分类正确率变化不大.实验结果表明基于置信优势关系粗糙集分类精度的属性约简方法在不完备有序信息系统中是有效的.

表3 约简前后分类正确率对比/%

总体来说,启发式约简方法和增量式约简方法有效,在数据样本较多时,增量式方法时间效率上更优.

6 总 结

对于不完备有序决策系统,本文在置信优势关系粗糙集的基础上,提出基于分类精度的启发式约简算法,由于每次增加或删除一个属性,启发式约简方法都需要重新计算整个论域的近似域得到分类精度,为此,给出增量式分类精度算法,从而得到增量式约简方法.对比实验表明,两个方法在属性约简上是有效的,在样本较多时,增量式约简方法更优.

[1] Dembczynski K,Greco S,Kotlowski W,et al.Quality of rough approximation in multi-criteria classification problems[C].Rough Sets and Current Trends in Computing,Springer Berlin Heidelberg,2006:318-327.

[2] Greco S,Matarrazzo B,Slowinski R.Rough approximation by dominance relations[J].International Journal of Intelligent Systems,2002,17(2):153-171.

[3] Pawlak Z,Skowron A.Rudiments of rough sets[J].Information Sciences,2007,177(1):3-27.

[4] Gou Guang-lei,Wang Guo-yin,Li Jie,et al.Confidential dominance relation based rough approximation model[J].Control and Decision,2014,29(7):1325-1329.

[5] Chang Li-yun,Wang Guo-yin.An approach for attribute reduction and rule generation based on rough set theory[J].Journal of Software,1999,10(11):1206-1211.

[6] Zhang Wen-xiu,Mi Ju-sheng,Wu Wei-zhi.Knowledge reduction in inconsistent information systems[J].Chinese Journal of Computers,2003,26(1):12-18.

[7] Xu Wei-hua,Zhang Wen-xiu.Methods for knowledge reduction in inconsistent ordered information systems[J].Journal of Applied Mathematics and Computing,2008,26(1):313-323.

[8] Xu Wei-hua,Li Yuan,Liao Xiu-wu.Approaches to attribute reductions based on rough set and matrix computation in inconsistent ordered information systems[J].Knowledge Based Systems,2012,27(3):78-91.

[9] Inuiguchi M,Yoshioka Y.Several reducts in dominance-based rough set approach[M].Interval/Probabilistic Uncertainty and Non-Classical Logics,Springer Berlin Heidelberg,2008:163-175.

[10] Kusunoki Y,Inuiguchi M.A unified approach to reducts in dominance-based rough set approach[J].Soft Computing,2010,14(5):507-515.

[11] Susmaga R.Reducts and constructs in classic and dominance-based rough sets approach[J].Information Sciences,2014,271(7):45-64.

[12] Gou Guang-lei,Wang Guo-yin.Inconsistent dominance principle based attribute reduction in ordered information systems[C].10th International Conference on Rough Set and Knowledge Technology,Tianjin,China,LNCS Volume,2015,9436:110-118.

[13] Chen Hong-mei,Li Tian-rui,Cai Yong,et al.Parallel attribute reduction in dominance-based neighborhood rough set[J].Information Sciences,2016,373(12):351-368.

[14] Shao Ming-wen,Zhang Wen-xiu.Dominance relation and rules in an incomplete ordered information system[J].International Journal of Intelligent Systems,2005,20(1):13-27.

[15] Yang Xi-bei,Yang Jing-yu,Wu Chen,et al.Dominance-based rough set approach and knowledge reductions in incomplete ordered information system[J].Information Sciences,2008,178(4):1219-1234.

[16] Yang Xi-bei,Yu Dong-jun,Yang Jing-yu,et al.Dominance-based rough set approach to incomplete interval-valued information system[J].Data & Knowledge Engineering,2009,68(11):1331-1347.

[17] Gou Guang-lei,Wang Guo-yin.An approach to knowledge reduction based inconsistent confidential dominance principle relation[J].Computer Science,2016,43(6):6-9.

附中文参考文献：

[4] 苟光磊,王国胤,利 节,等.基于置信优势关系的粗糙集近似模型[J].控制与决策,2014,29(7):1325-1329.

[5] 常犁云,王国胤.一种基于Rough Set 理论的属性约简及规则提取方法[J].软件学报,1999,10(11):1206-1211.

[6] 张文修,米据生,吴伟志.不协调目标信息系统的知识约简[J].计算机学报,2003,26(1):12-18.

[17] 苟光磊,王国胤.基于不协调置信优势原理关系的知识约简[J].计算机科学,2016,43(6):6-9.