一种支持向量机算法设计中优化的混合加权核函数选取与样本加权方法

曹万鹏,罗云彬,史 辉

(北京工业大学 未来网络科技高精尖创新中心,北京 100124)

1 引 言

今天,科研人员已经提出各种成熟的数学分类模型,诸如ID3,C4.5,SVM,朴素贝叶斯(Native Bayes),AdaBoost和K-最近邻(k-Nearest Neighbor),ANN(人工神经网络)等分类算法,并基于上述思想,将它们应用到面部识别[1,2]、笔迹验证[3,4]、数据分析[5,6]和医学应用[7,8]等不同领域.近年来,基于SVM的分类算法因其结构简单、泛化能力强、学习和预测时间短、能实现全局最优等卓越性能而应用于诸多领域,特别是在处理小样本、非线性和高维模式识别问题上.

在SVM算法中,通过将原始样本空间的非线性问题转化为高维空间中的线性问题,可以成功地解决分类问题.这里,非线性变换是利用满足Mercer条件的核函数实现的.在SVM模型设计中合适的核函数选择和训练样本权值设置都很重要,共同决定了分类器性能的优劣.寻找更为合适的核函数,并为训练样本设置更加合理权值等已成为研究热点.

近年来,人们提出不同算法尝试为SVM算法选取一个恰当的单一核函数.吴涛等基于可以将核函数结构视为函数插值问题这一假设通过训练样本构造合适的核函数[9].Wu等采用一种混合遗传算法(HGA)优化核函数,进而提高SVM算法模型的准确性[10].You等使用三个主要指标:Fisher判别,Bregman散度和方差齐性从矩阵中抽取特征进行核函数的选择[11].Keerthi等人应用双线性方法遍历核函数的参数集,实现核函数中参数的最优设计[12].Maji等人设计了一种自适应的支持向量机核函数,达到了提高SVM分类模型分类性能的目标[13].尽管单一核函数在某些情况下对于分类模型的学习要求已经足够,但仅依靠单一核函数构建SVM分类模型经常不能实现最佳分类效果.当前,研究人员越来越多地使用混合核函数,并已经证明将不同功能核函数组合在一起的方法可实现更优SVM模型设计,更好分类性能[14].

对混合核函数的研究中,最常用的方法是结合全局核函数和局部核函数来构造混合核函数.Wu等[15]和Huang等[16]都选择了这种方法,因为基于局部核函数的学习能力和全局核函数的良好泛化能力所构建混合核函数相对于单一核函数方法或一般组合核函数方法具有更好的性能.许多学者把RBF核函数和多项式核函数作为局部核函数和全局核函数进行混合核函数的设计,并将其成功地应用于不同工作中,获得了令人满意的分类效果[17-19].

一些研究者也采用了不同的方法构建混合核函数.Zhu等详细分析了核函数设计对分类性能的影响因素,基于Fisher特征与核函数矩阵校准方法的结合,对单一核函数性能进行预测,并在此基础上构造了一种新的用于人脸识别的混合核函数,取得了令人满意的结果[20].Xie通过分析现有LS-SVM核函数并吸收RBF核函数和多项式核函数的优点构建混合核函数,改进了现有的LS-SVM算法[21].Üstün等则采用了基于Pearson VII的通用函数(PUK),实验证明PUK核与标准核函数相比具有同等或更强大的映射能力,进而导致同等或更好的SVM泛化性能[22].Gönen等人通过实验比较了现存的混合核函数方法,并证明了用混合核函数的方法在性能上要优于单一核函数构建SVM分类模型的方法[23].

目前,同步研究在候选核函数中选取哪些核函数,并且为这些核函数设置什么样权值的文献并不多见.大多数混合核函数算法直接选择RBF核函数和多项式核函数构造混合核函数,没有进行相应的学习与分析,这不可避免的导致了不尽理想的分类效果.而且大多数混合核函数的构造方法往往缺乏有效的反馈机制来指导混合核函数的设计,也很少考虑如何基于样本特征为不同核函数设置更为合理的系数.基于此,本文采用ACO算法实现混合加权核函数中相关核函数和对应系数的优化选取.此外,因为SVM分类模型最大分类间隔决定了分类的确定性和所学习分类模型对后续样本的潜在分类性能,在SVM分类模型的设计过程中,为进一步提高分类模型的分类能力,本文基于训练样本对SVM分类模型最大分类间隔的贡献对训练样本进行自适应权值设置.

本文第2节介绍了SVM算法和组合核函数;第3节建立了基于当前训练样本特征的自适应样本加权算法;第4节根据SVM分类原理设计了改进的ACO算法,实现了优化混合加权核函数的选择;第5节完成了本文方法的实验验证和相应的实验分析;第6节对本文工作进行了总结.

2 SVM算法与混合核函数原理介绍

SVM算法核心思想是寻找一个满足分类要求的最优分类超平面,具体的分类原理如图1所示.

给定训练集(xi,yi),i=1,2,…,N,x∈Rn,y∈{±1},超平面为w·x+b=0.为使分类超平面正确分类所有样本并产生一个尽量大的分类间隔,需满足方程:

yi[(w·xi)+b]≥1,i=1,2,…,N

(1)

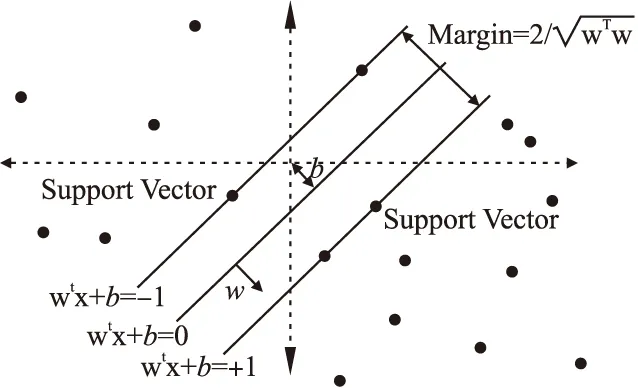
图1 SVM算法结构图Fig.1 SVM algorithm structure diagram

因此,分类间隔可表示为2/‖w‖,构造最优超平面的问题则转化为下列约束的最小值问题:

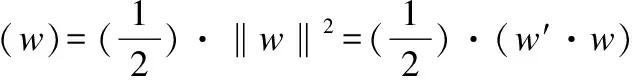
(2)

这里,引入拉格朗日函数,

(3)

公式(3)中,αi是拉格朗日系数,且有αi>0.该约束优化问题由拉格朗日函数鞍点确定,优化问题的解满足在鞍点处对w和b的偏微分为0.最后,QP(二次规划)问题转化为相应的对偶问题:

(4)

这里,满足,

(5)

通过计算,最优权值向量w*和最佳偏置b*分别为:

(6)

那么,最优分类平面为:

w*·x+b*=0

(8)

最优分类函数为:

(9)

在这里,x∈Rn.当样本非线性可分时,输入特征空间通过非线性变换变换到一个高维特征空间.为了在高维空间中寻求最佳线性分类,通过定义适当的内积函数(核函数)实现非线性变换.SVM算法可以用训练集和核函数完全描述,训练集和核函数是决定算法成败的关键.因此,将训练样本映射到其他空间,实现线性区分处理,分割效果取决于核函数的选择.不同核函数K的选择将导致完全不同的SVM算法,决定了所构建分类模型的分类性能,在SVM算法中起着决定性作用.非线性SVM的最优分类函数如下:

(10)

这里,K(x·xj)表示核函数.本文选取6个最常用的高性能核函数作为候选核函数,公式具体如下:

1)多项式核函数:

(11)

2)径向基核函数:

(12)

3)Sigmoid核函数:

(13)

4)线性核函数:

K(xi,xj)=xi·xj

(14)

5)傅里叶核函数:

(15)

6)样条核函数

K(xi,xj)=B2n+1(xi-xj)

(16)

那么,本文中混合加权核函数可以设计为:

K(xi,xj)=∑lclKl(xi,xj),l=1,2,…,6

(17)

同时,为了确保混合核函数不改变原始匹配的合理性,通常有接下来的约束公式[24]:

(18)

在这里,cl是核函数组合中第l个核函数的加权系数,而Kl(xi,xj)表示6个候选核函数中的第l个核函数.

3 基于当前样本对SVM最大分类间隔贡献度的自适应样本加权方法

为进一步改进对分类模型的学习,本文构建了一种基于训练样本特征的自适应加权方法.为所有样本设置统一的权值在SVM分类模型构建中显然并不恰当,而基于当前样本特征为不同样本设置不同权值可以提高分类模型分类性能.为此,本文提出一种自适应样本加权方法,它基于当前样本对SVM分类模型最大分类间隔的贡献,从提高分类确定性和分类模型对待检测样本正确分类能力的角度构造分类模型.

如何为训练样本设置自适应加权系数是决定分类器性能的关键.从SVM分类原则出发,SVM算法中最大分类间隔决定了分类的确定性程度.对后续待检测样本,更大的最大分类间隔代表着更好的潜在正确分类能力和更大的正确分类冗余[25].因此,就分类性能而言最大分类间隔越大,分类性能越佳.一般情况下,使被构造分类器最大分类间隔增加的训练样本,有利于分类器潜在分类能力的提升,应为其设置更大权值.相反,使最大分类间隔降低的训练样本应该指定较小权值.本文设计思想是计算训练样本对最终SVM分类器最大分类间隔的贡献度,进而根据该信息为其设置恰当权值.因此,训练样本自适应加权系数hj设计如下:

(19)

这里,假设do是基于全部训练样本学习的SVM分类模型而获得的对应最大分类间隔,dj是通过从全部训练样本中去除当前训练样本后获得的新的最大分类间隔,Δdj是do与dj的差值,Δdmax为所有Δdj中最大的最大分类间隔增量.hj可通过以下步骤获得:

步骤1.使用所有训练样本,包括当前样本,基于SVM算法计算初始最大分类间隔do;

步骤2.基于SVM算法,使用除当前第j个样本外剩余训练样本计算得到最大分类间隔dj;

步骤3.使用公式Δdj=do-dj计算由样本j引起的最大分类间隔的增量Δdj;

步骤4.重复步骤2和步骤3,直到获得所有的M个训练样本对最大分类间隔的贡献度;

步骤5.在Δdj中选择最大的最大分类间隔增量Δdmax;

步骤6.由公式(19),给出每个样本的自适应权值hj;

步骤7.结束加权系数的计算,并通过相应的自适应权值加权所有这些训练样本.

通过训练样本权值更新系数hj为导致SVM最大分类间隔增量增大的样本设置更高权值.因为有利于提高分类模型分类性能的训练样本通过自适应加权,获得了更大权值,它们在分类器构建中也将发挥更大作用,所以通过本文加权方法构建的分类模型比非加权方法获得了更优分类性能.

4 基于改善的ACO参数设置算法的最优混合加权核函数搜索

从一系列候选核函数中选择恰当的核函数,并为它们设置合理的权值对提高分类器分类性能异常关键.基于ACO算法在搜索参数空间中寻找最佳参数的优势,本文采用ACO算法,并在算法参数设置中引入最大分类间隔因素,为SVM分类模型寻找最优核函数组合及其对应的核函数系数.

ACO算法是将待求解计算问题简化为搜索最佳路径的概率算法.最初,该算法的设计是模拟蚂蚁的行为,即它们在巢穴和食物源之间寻找一条最佳路径的行为.从更广泛的角度来看,ACO算法可用于执行模板基的搜索算法[26].

ACO参数的合理设置对于为实际问题所建立的数学模型寻找最佳系统参数异常重要.本文中,根据SVM分类算法基本原理,设计更为合理和有针对性的ACO参数设置方案,用以决定选择哪些核函数并为它们设置多大权值,进而获得更优的混合加权核函数.同时,不同于其他参数设置方法,为充分反映分类模型的潜在分类能力和分类确定性,将最大分类间隔因素引入到ACO参数设置中,对其改进如下:

(20)

这里,i和j分别表示路径上节点i和j,ρij是路径上节点i和j的信息素挥发系数,k表示第k条路径,dk表示路径k上的最大分类间隔,dmax对应着所有最大分类间隔中的最大值,M是路径数.同时,为进一步反映和强调分类间隔因素在ACO搜索中的重要性,启发式信息ηij设置为:

ηij=1-ρij

(21)

从这两个公式中可以看到,较大的最大分类间隔对应于一个较小的信息素挥发系数和一个较高的转移概率.很明显,这会引导蚂蚁(训练样本)聚集向一条对应较大最大分类间隔的路径.最终,基于这种改进参数设置的ACO算法会获得更优的核函数组合及对应加权系数.本文所提出算法对应流程图如图2所示:最后,根据改进的ACO参数设置,将给出更为合理核函数组合和对应加权系数,具体步骤如下:

步骤1.初始化相关参数:

1)设置全部蚂蚁(训练样本)的信息素τ初始值为常量,并将全部蚂蚁放置于蚁巢;

2)设置ACO算法搜索的最大次数为Nmax;

3)设置蚂蚁数为S,每个蚂蚁包括n个参数,对应着蚂蚁觅食路径上的n个节点.

步骤2.选择每个“节点”(表示每一个不同的候选核函数和不同的加权系数)作为一个路径;

步骤3.记录路径中核函数、相应系数的选择,在到达目的地后得到混合加权核函数,更新搜索次数N=N+1;

步骤4.根据学习得到的SVM模型,利用相应的组合加权核函数,计算分类模型的分类精度和最大分类间隔;

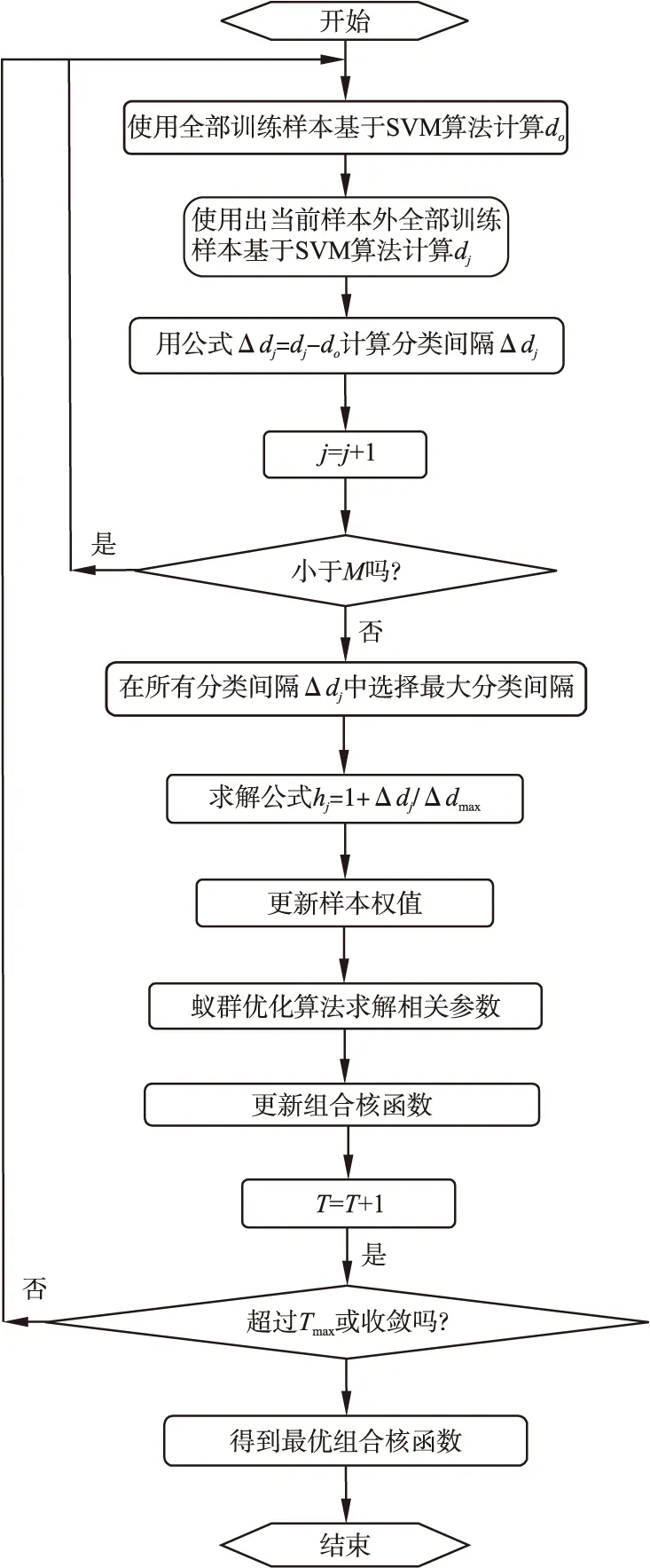
图2 算法流程图Fig.2 Proposed method flow chart

步骤5.基于分类精度和分类间隔更新信息素τ,信息素τ更新如下:

(22)

转移概率p更新如下:

(23)

步骤6.当所有的蚂蚁没有收敛到一条路径或搜索次数小于预设的最大迭代次数时,继续重复步骤2到步骤4;

步骤7.结束对核函数及其相应权值的搜索,并给出基于当前训练样本的最优核函数组合及相应核函数系数.

通过结合上文中提出的基于当前样本对最大分类间隔贡献的自适应样本加权方法和本部分提出的基于改进ACO参数设置的最优组合加权核函数选择方法,学习SVM分类模型,可获得分类性能更加卓越的SVM分类模型.

5 实验验证与分析

在这部分中,通过一系列实验验证本文方法的分类性能,实验使用中文笔迹样本进行验证,样本来自于哈尔滨工业大学开放手写文本库HIT-MW[27].它提供来源于240个不同人的中文笔迹样本,每个人笔迹为不同内容,如图3所示.

图3 从开放笔迹库随机选取的4份笔迹样本Fig.3 Four Chinese handwriting samples randomly taken from open handwritten text library

同时,为验证所学习分类模型分类性能,本文采用李昕的笔迹特征抽取算法[28],该方法经验证对于提取笔迹细节特征具有很好性能.通过该方法从笔迹样本中提取一系列微结构特征作为样本多维特征用于SVM分类模型的学习.然后,使用本文算法设计分类器,通过5个有针对性的验证实验,从多个角度对本文算法进行了验证、分析.

第1个验证实验采用交叉验证方式对对应不同最大分类间隔的SVM分类模型进行验证,考察最大分类间隔因素对SVM分类模型分类性能的影响.在样本库中,首先随机选择100个笔迹实例作为训练样本并将其等分为10份.然后,使用这10组样本采用不同算法分别学习SVM分类模型,获得10个分类器,并求解它们所对应的最大分类间隔.另外,再选取100个笔迹样本,等分为10份作为后续测试样本.用这10个新构建分类器分类测试样本,计算它们对应的平均分类精度.

为增加实验的一般性,每次更换训练样本、测试样本,重复上述实验10次,可方便地获得SVM分类模型的最大分类间隔与对应分类精度之间的关系.10个分类器中,两两比较对应不同最大分类间隔的SVM分类模型所获得分类精度.设某次进行比较的两个分类器分别为Ci和Cj,由(Ci,Cj)表示,模型Ci对应的最大分类间隔di,Cj对应的最大分类间隔为dj,max(Δdij)表示两分类器对应的较大最大分类间隔与较小最大分类间隔的差值,其值大于等于0,表1给出了对比结果.表1中,“获胜”代表两分类器精度比较中,对应较大最大分类间隔的分类器所获得的分类精度不小于对应较小最大分类间隔的分类器所获得的分类精度;“失败”则代表两分类器精度比较中,较大最大分类间隔的分类器所对应分类精度小于对应较小最大分类间隔的分类器所对应分类精度.从表1可看到,对应较大最大分类间隔的分类模型(max(Δdij)大于等于0)在分类精度的45次比较中赢了42次.实验结果证明了具有较大分类间隔的SVM分类模型对后续未知测试实例具有更强分类能力.

表1 分类精度比较结果
Table 1 Comparison outcome on classification accuracy

进行比较的两分类器max(Δdij)获胜次数失败次数(Ci，Cj)大于等于0423

为进一步验证基于本文样本加权方法所构建SVM分类模型对于待检测样本拥有更大的正确分类确定性,根据上文方法多次重复胜负比较实验,对比本文样本加权方法与非样本加权方法分别构建的分类模型的分类精度高低.表2给出了采用这两种方法构建分类模型的比较结果,可以看到,本文方法几乎赢得了所有的比较.同时,当测试样本数量增加时,用本文算法学习的SVM分类器获胜面更大.这是因为从增加SVM分类器最大分类间隔的角度设计的样本加权方法使所构建分类模型最大分类间隔增加.当训练样本增多时,这种改进将更加明显,进而使所构建SVM分类模型与传统方法相比具有更强正确分类能力.

表2 加权方法对非加权方法基于分类精度的获胜率 (%)
Table 2 Classification accuracy win ratio (%)

分类模型5样本10样本15样本20样本25样本训练样本加权方式构建的分类器模型94．2095．5197．7198．3798．73

在第2个测试实验中,从笔迹样本库中随机选取100个样本,等分为10份.然后,训练10组笔迹样本获得10个SVM分类模型.每次,取其中的9个训练样本训练分类模型,把另外1个样本作为测试样本,重复10次,计算平均分类精度.表3给出了使用本文样本加权方法和非加权方法构建的分类模型对应的平均分类精度.

表3 样本加权方法vs非样本加权方法的分类精度比较(%)
Table 3 Classification accuracy for the sample weighting method vs sample unweighting method (%)

方法MeanClassificationAccuracy样本加权方法94．63非样本加权方法92．86

从表3可以看到,用样本加权算法学习到的分类模型拥有更高分类精度.实验结果证明,基于SVM最大分类间隔增量为测试样本设置权值系数,因为对应较大最大分类间隔增量的样本被指定了更大权值,进而导致该样本在分类模型构建中发挥了更大作用,使对分类模型的学习更倾向于提高SVM的最大分类间隔,该方法有益于所构建分类模型分类精度的改善,对后续待检测样本具有更强的正确分类能力.

在第3个验证实验中,为验证在ACO算法参数设置中引入SVM最大分类间隔因子对所构建分类器分类性能的正向影响,基于两种不同参数设置方法求解最优核函数组合和对应加权系数.两种方法共同的参数设置如下:信息素τ和Q(信息素强度)的初始值设置为10和100,最大迭代次数设置为500,α值(激励因素),β(期望启发式因子)分别设为1和5.不同设置为,第一个方法对最优候选核函数和相应参数的ACO搜索使用传统方法,将信息素设置为与分类精度相关,其他参数设置为常量.在第二个ACO参数搜索中,使用公式(20)至(23)设置相关ACO参数,包括挥发系数ρ,启发信息η,信息素τ和转换概率p.然后,分别根据两个具有不同参数设置的ACO算法搜索混合核函数,并比较由不同搜索学习的分类模型的分类精度.

另外,随机选取50个笔迹样本作为蚂蚁,设置6个候选核函数(公式(11)-(16))和它们全部可能对应系数(0,0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,1)为ACO搜索路径中的节点.进而,ACO中的每条路径选择对应一个混合加权核函数方案的选取,如图4所示.

图4 本文ACO算法的简化示意图Fig.4 Designed simplified ACO sketch map

这里,Ki表示候选核函数,Wi表示核函数系数,虚线表示路径.通过两种不同参数设置的ACO算法对候选核函数与其系数进行搜索,获得两条不同路径,代表着两个不同的混合加权核函数选择方案.用这两个选择方案分别学习SVM分类模型,计算对应分类器的分类精度.

实验中,第1种ACO算法命名为方法1,参数设置引入SVM最大分类间隔因素.根据公式(20),最大分类间隔越大,则信息素蒸发速度越慢.相应地,启发信息ηij更强.第2种ACO算法命名为方法2,该方法不在参数设置中考虑最大分类间隔因子.在相同条件下,使用上述两方法搜索网络中的最佳路径.为了验证最大分类间隔因素的引入对分类模型正确分类的能力的提升,这个实验使用不同数量的验证样本.对应结果显示在表4和图5中.表4给出了用两种ACO参数设置方法构建的分类模型分类精度的比较.实验结果展示出因为搜索中考虑了最大分类间隔因素,使所构建分类模型在分类精度上有了较大改善.

从图5可以看到,相对于传统的ACO参数设置方法,本文所提出参数设置方法的优势主要体现在通过学习所得的SVM模型对后续未知检测样本的正确分类能力.这是因为ACO算法中最大分类间隔因子的引入改善了算法的优化方向,使基于此方法所设计SVM分类模型倾向于产生一个更大的最大分类间隔,进而提高模型正确分类性能.

第4个验证实验讨论了核函数加权方法对所构建分类模型分类性能的影响.从样本库中随机选取100个样本并等量地将其分为10组.然后,通过训练10组样本对SVM分类模型进行学习,获得10个分类模型.每次,用其中9个训练样本建立分类模型,把另外1个样本作为测试样本.重复此过程10次,计算平均分类精度.相同情况下,基于同样步骤采用核函数系数加权方法和非加权方法分别构建混合核函数,并用上述不同混合核函数分别学习SVM分类模型,求解对应的平均分类精度.

表4 不同训练样本下本文提出ACO算法 vs 传统 ACO算法的分类精度比较 (%)
Table 4 Classification accuracy for the proposed ACO vs traditional ACO from the different number of test samples (%)

精度5样本10样本15样本20样本25样本30样本35样本方法194．4394．6595．1394．8894．3593．8994．67方法293．2893．6291．5791．9991．1489．1790．35

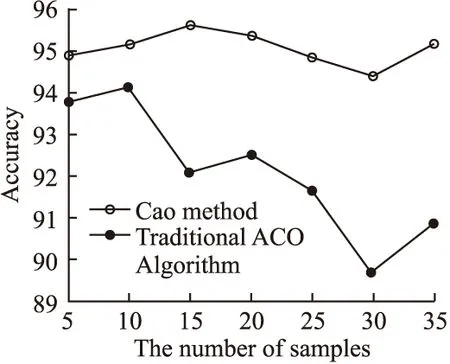
图5 本文提出ACO算法 vs 传统 ACO算法Fig.5 Proposed method vs traditional ACO method

表5给出了分别用这两种方法获得的分类精度,从表5看到,基于混合加权核函数构建的分类模型比非加权方法获得了更好分类效果.实验结果也反映出基于对最优分类性能的追求,有必要在混合加权核函数设计中为不同核函数赋予不同系数.因为设置统一系数的混合核函数尽管实现了输入特征空间到高维特征空间的变换,但这一变换并不是所有变换中最优的变换,也不能实现最优SVM分类模型的学习.因此,统一的系数设置明显不够合理,难以获得满意效果.

表5 核函数加权方法vs非加权方法的分类精度比较(%)
Table 5 Classification accuracy for the kernel function weighting method vs unweighting method (%)

方法平均分类精度核函数加权方法94．47核函数非加权方法93．03

对于第5个验证实验,依然从样本库随机选取100个笔迹样本并分为等量的10组.然后,通过训练10组样本对SVM分类模型进行学习,获得10个分类模型.每次用不同数量训练样本,重复该过程10次,计算平均精度.相同情况下,基于同样步骤采用样本加权方法学习分类模型,用本文算法和另外3种核函数构建算法分别学习分类模型.3种方法分别为上文中介绍的Wu[9],Huang[16]和Xie[21]所提出方法.同时,这4种方法一同用于分类相同测试样本以验证和比较它们的分类性能.训练样本数量按步长1从4个增加到10个,考察不同数量训练样本下所构建分类模型性能.4种方法分类精度差异效果显示在表6和图6.

表6 不同数量训练样本下本文算法vs另外3种算法(%)
Table 6 Classification accuracy for the proposed method vs other three methods based on the different number of training samples (%)

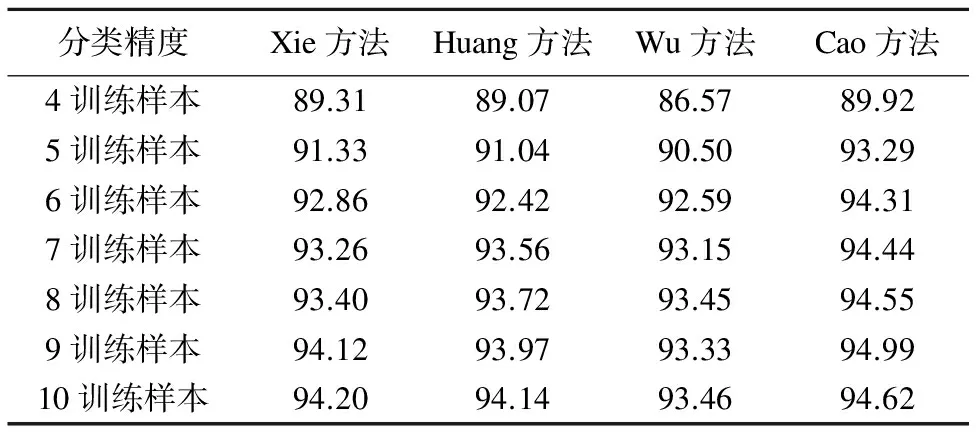
分类精度Xie方法Huang方法Wu方法Cao方法4训练样本89．3189．0786．5789．925训练样本91．3391．0490．5093．296训练样本92．8692．4292．5994．317训练样本93．2693．5693．1594．448训练样本93．4093．7293．4594．559训练样本94．1293．9793．3394．9910训练样本94．2094．1493．4694．62

从表6可以看出,无论使用多少训练样本,与其他3种核函数构建方法相比,本文提出的方法具有更高分类精度.即使在可获得训练样本较少的情况下,本文方法仍然可以训练出性能优良的分类器,并可取得令人满意的分类精度.

从图6还可以看出,随着训练样本数的增加,各种方法的分类精度均有不同程度的改善.当样本数继续增加时,分类精度增加速度逐渐放缓.本文方法与其他3种方法相比,能更快速地达到较高分类精度.当训练样本数超过5后,本文算法的精度变化已很小.显然,本文算法的分类性能明显优于其他方法,这是因为本文算法是从SVM的构建原理和分类原则出发设计的,从根本上提高了SVM分类模型性能.

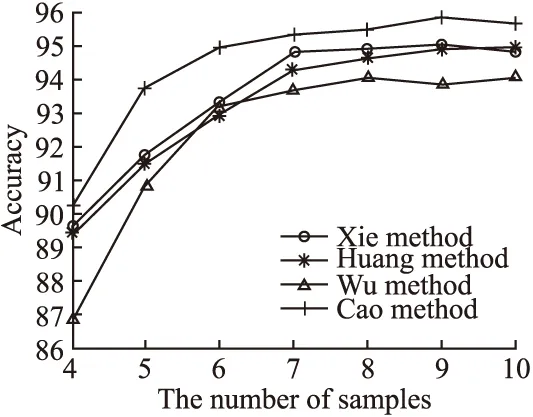
图6 本文提出方法vs对另外3种方法Fig.6 Proposed method vs other three methods

通过上述5个有针对性的实验验证了本文算法的有效性,实验结果也证明了本文所提出方法的良好性能,并进一步显示出本文算法的有效性.

6 结 论

在本文中,提出了一种基于ACO算法的最优混合加权核函数构建方法和一种新的基于当前样本特征与SVM分类模型工作原理的训练样本权值设置方法.本文首先根据样本对SVM分类模型最大分类间隔的贡献,建立了一种基于训练样本特征的自适应样本加权方法.它基于SVM算法原理设计,因此所构建分类模型分类性能更强.实验证明,通过不同权值设置,算法提高了正确分类能力,有利于提高SVM分类器对待检测样本的潜在正确分类能力,进而提高分类器的整体分类性能.

除样本加权方法,本文还利用ACO算法寻找加权核函数组合的最佳方案.不同于其他ACO搜索算法,本文中ACO参数设置中引入了最大分类间隔因素,从SVM算法原理上提高了对后续样本正确分类的能力,实验结果也验证了上述算法.同时,改进的参数设置因为综合考虑了分类器学习中分类精度和最大分类间隔指标因素,使所学习SVM分类模型具有更佳的分类性能.

[1] Khan N,Ksantini R,Ahmad I,et al.A novel SVM+NDA model for classification with an application to face recognition[J].Pattern Recognition,2012,45(1):66-79.

[2] Kasar M,Bhattacharyya D,Kim T.Face recognition using neural network:a review[J].International Journal of Security and Its Applications,2016,10(3):81-100.

[3] Hasseim A,Sudirman R,Khalid P.Handwriting classification based on support vector machine with cross validation[J].Engineering,2013,5(5B):84-87.

[4] He Z,You X,Tang Y.Writer identification of Chinese handwriting documents using hidden Markov tree model[J].Pattern Recognition,2008,41(4):1295-1307.

[5] Dhillon S,Kaur K.Comparative study of classification algorithms for web usage mining[J].International Journal of Advanced Research in Computer Science and Software Engineering,2014,4(7):137-140.

[6] Liu B,Blasch E,Chen Y,et al.Scalable sentiment classification for big data analysis using Naïve Bayes classifier[C].IEEE International Conference on Big Data,2013:99-104.

[7] Bendi V,Surendra P,Venkateswarlu N.A critical study of selected classification algorithms for liver disease diagnosis[J].International Journal of Database Management Systems,2011,3(2):101-114.

[8] Raikwal J,Kanak S.Weight based classification algorithm for medical data[J].International Journal of Computer Applications,2014,107(21):1-5.

[9] Wu Tao,He Han-gen,He Ming-ke.Interpolation based kernel function′s construction[J].Chinese Journal of Computers,2003,26(8):990-996.

[10] Wu C,Tzeng G,Lin R.A Novel hybrid genetic algorithm for kernel function and parameter optimization in support vector regression[J].Expert Systems with Applications,2009,36(3):4725-4735.

[11] You D,Hamsici O,Martinez A.Kernel optimization in discriminant analysis[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2011,33(3):631-638.

[12] Keerthi S.Efficient tuning of SVM hyperparameters using radius/margin bound and iterative algorithms[J].IEEE Transactions on Neural Network,2002,13(5):1225-1229.

[13] Maji S,Berg A,Malik J.Efficient classification for additive kernel svms[J].IEEE Transaction on Pattern Analysis and Machine Intelligence,2013,35(1):66-77.

[14] Smits G,Jordan E.Improved SVM regression using mixtures of kernels[C].International Joint Conference on Neural Networks,2002,3:2785-2790.

[15] Wu F,Ding S.Twin support vector machines based on the mixed kernel function[J].Journal of Computers,2014,9(7):1690-1696.

[16] Huang H,Ding S,Jin F,et al.A novel granular support vector machine based on mixed kernel function[J].International Journal of Digital Content Technology & its Applic,2012,6(20):484-492.

[17] Zheng S,Liu J,Tian J.An efficient star acquisition method based on SVM with mixtures of kernels[J].Pattern Recognition Letters,2005,26(2):147-165.

[18] Yang X,Peng H,Shi M.SVM with multiple kernels based on manifold learning for breast cancer diagnosis[C].IEEE International Conference on Information and Automation,2013:396-399.

[19] Kavzoglu T,Colkesen I.A kernel functions analysis for support vector machines for land cover classification[J].International Journal of Applied Earth Observation and Geoinformation,2009,11(5):352-359.

[20] Zhu Y,Liu W,Jin F,et al.The research of face recognition based on kernel function[J].Applied Mechanics and Materials,2013,321-324(8):1181-1185.

[21] Xie J.Time series prediction based on recurrent LS-SVM with mixed kernel[C].Asia-pacific Conference on Information Processing,2009,1:113-116.

[22] üstün B,Melssen W,Buydens L.Facilitating the application of support vector regression by using a universal Pearson VII function based kernel[J].Chemometrics and Intelligent Laboratory Systems,2006,81(1):29-40.

[23] Gönen M,Alpaydm E.Multiple kernel learning algorithms[J].Journal of Machine Learning Research,2011,12:2211-2268.

[24] Wang G.Properties and construction methods of kernel in support vector machine[J].Computer Science,2006,33(6):172-174.

[25] Li Hang.Statistical learning method[M].Beijing:Tsinghua University Press,Beijing,2012.

[26] Nada M.System evolving using ant colony optimization algorithm[J].Journal of Computer Science,2009,5(5):380-387.

[27] Su T,Zhang T,Guan D.Corpus-based HIT-MW database for offline recognition of general-purpose Chinese handwritten text[J].International Journal on Document Analysis and Recognition,2007,10(1):27-38.

[28] Li Xin,Ding Xiao-qing.Writer identification based on improved microstructure features[J].Journal Tsinghua University (Sci & Tech),2010,50(4):595-600.

附中文参考文献：

[9] 吴 涛,贺汉根,贺明科.基于插值的核函数构造[J].计算机学报,2003,26(8):990-996.

[25] 李 航.统计学习理论[M].北京:清华大学出版社,2012.

[28] 李 昕,丁晓青.基于改进微结构特征的笔迹鉴别[J].清华大学学报(自然科学版),2010,50(4):595-600.