一种改进共同邻居的节点遍历链路预测算法

张志刚,李世宝,马文丽,何 雅,陈海华,刘建航

(中国石油大学(华东) 计算机与通信工程学院,山东 青岛 266580)

1 引 言

自然界中存在的大量复杂系统均可以抽象成由相互连接的节点所组成的复杂网络,其中节点代表个体,链接反映个体之间的相互联系,譬如社交网络、生物网络、交通网络.通过对复杂网络进行研究,我们可以更好的理解网络结构生成和演化机制,也可以用来解决实际复杂系统中的问题.链路预测是连接复杂网络与信息科学的重要纽带,已成为复杂网络研究中的热点之一,其目的是基于已知的链接和节点属性以及网络拓扑结构对未知链接进行还原和预测[1].

链路预测可以对实际复杂系统中存在但未被我们观察到的链接(遗失链接)[2]和将来可能产生的链接(未来链接)进行预测,对复杂系统的研究有巨大的实际应用价值[3].在蛋白质作用网络中,有80%的相互作用关系是人类尚未挖掘出来的[4],可以利用链路预测的方法挖掘那些隐而未露的相互作用,可以降低实验成本[5].在电子商务网络中,可以为用户推荐感兴趣的商品.在科学家合作网络中,可以对科学家之间潜在合作的可能性进行预测.链路预测的相关技术可用于在线社交网络中的朋友推荐[6],也可以用来识别网络中的虚假链接[7].毫无疑问,链路预测相关研究具有较高的商业应用价值,因此成为近年来研究的热点和重点之一.

本文通过分析传统链路预测算法存在的问题,综合考虑影响链接形成的因素,通过利用节点间共同邻居的平均度以及网络中每个节点的对链接产生的贡献,提出了一种同时兼顾预测精度和普适性的相似性指标.

2 相关工作

目前链路预测相关的研究渐渐趋于成熟,各种各样的算法被相继提出.用于链路预测的算法模型主要分为三类:基于马尔科夫链、基于概率似然模型和基于拓扑结构的链路预测算法.其中基于马尔科夫链和基于概率似然的链路预测算法虽然在各种网络上都具有较好的预测精度,但是计算复杂度很高,不适合处理大规模网络.基于网络拓扑结构的链路预测算法则不存在上述问题,在保证预测精度较高同时也有较低的计算复杂度,而且拓扑结构信息容易获取,适用于处理当今大数据时代网络数据指数增长的网络.

基于拓扑结构的链路预测算法又可以分为基于局部信息的相似性指标、基于路径的相似性指标和基于局部信息改进的相似性指标.共同邻居指标(common neighbor,CN)[8]是基于局部信息的相似性指标中最简单的一种,该指标认为两个节点之间的共同邻居数目越多,则两个节点间产生链接的概率越大.对于网络中的两个节点Vx和Vy,定义其邻居集合分别为Γ(x)和Γ(y),则两个节点Vx和Vy的相似性定义为:

Sxy=|Γ(x)∩Γ(y)|

(1)

Leicht等人在CN的基础上考虑节点的度的作用提出了LHN指标[9],该指标认为两个节点间共同邻居越多,节点度的乘积越小,产生链接的概率越高,定义为:

(2)

Adamic等人考虑CN中的个体存在差异,提出了Adamic-Adar(AA)指标[10],考虑两个节点共同邻居的度的信息,根据共同邻居节点的度为每个节点赋予一个权重值,该权重等于该节点的度的对数的倒数,定义为:

(3)

其中Z代表节点x和节点y之间的共同邻居.Zhou等人根据复杂网络资源分配过程提出了资源分配(Resource Allocation,RA)指标[11],该指标将节点x和y的共同邻居看作是传递资源的中介,每个中介拥有一定的资源,并将其资源均分给其邻居,定义为:

(4)

并在多个网络上具有较好的预测精度.偏好连接相似性指标(preferential attachment,PA)[12]提出了链接产生的概率正比于该边两个节点度的乘积.基于路径的相似性指标中的局部路径(Local Path,LP)指标[13]是在CN的基础上考虑节点间路径长度为3的路径数目,预测精度有所提升.Katz指标[14]则是对LP指标的改进,考虑了网络中的所有路径.上述指标的优点是简单且计算复杂度低,但预测精度不高,因此目前有很多学者对基于局部信息的指标进行了改进.刘震等人在CN和RA指标的基础上组合局部贝叶斯模型(local naïve bayes,LNB)提出了LNB-CN和LNB-RA指标[15],LNB-CN指标在局部朴素贝叶斯模型的基础上,将CN指标和聚类系数组合在一起形成的新的预测指标,定义为:

(5)

(6)

在食物链网络中该指标的预测精度提高了14%.刘大伟等人提出了局部差异融合算法[16],该方法在AA方法的基础上考虑共同邻居集合内部的差异性;综合考虑基于局部信息指标的特点,Zeng提出了CN+PA的组合指标[17],该指标较传统的CN指标预测精度提高了约10%.上述指标都是在基于局部信息指标上做的改进,虽然目前已经取得了很多的研究成果,但仍有一些问题尚未被深入研究,因此本文将通过分析已有指标存在的问题提出一种基于共同邻居的改进算法.

传统基于局部信息的指标,仅仅考虑的是共同邻居的数量、共同邻居的度以及共同邻居之间的关系,并没有充分考虑节点间产生链接的因素,导致在某些网络上的预测精度较低,因此本文通过分析实际网络中存在的共同邻居中大度节点对于节点间产生连接的贡献较小的现象,在降低待预测节点间共同邻居的大度节点影响的同时结合网络中每个节点对于待预测的两个节点产生链接的贡献,提出一个针对无向无权网络的新的链路预测指标,通过大量的实验证明该指标相比传统的指标具有较好的普适性和较高的预测精度.

3 链路预测问题描述及相似性指标

3.1 链路预测问题描述

链路预测是在已知网络拓扑结构和节点属性的基础上预测网络中没有观察到的链接产生的可能性.针对链路预测问题,首先要利用图论的相关知识将真实的网络抽象成复杂网络,对于一个无向无权的复杂网络,可以用图论的理论G(V,E)进行表示,其中V={V1,V2,V3,…,Vn}代表网络中n个节点的集合,E={e1,e2,e3,…,em}代表含有的m条边(链接)的集合,其中任意一条边对应于一个节点的二元组:ex={Vi,Vj};节点Vi的度记为ki,即包含节点Vi的边的数目.U代表包含所有可能的n(n-1)/2条连边的集合,目前不存在的连边(将来有可能存在)的集合为U-E,假设不存在的连边集合U-E中存在一些遗失的链接,链路预测的目的就是找出那些遗失的链接.如图1所示,假设一个实际的网络是由六个节点

图1 链路预测问题示意图Fig.1 Link prediction problem

以及七条链接组成,在观察到的网络AO中遗失了链接(1,5),遗失的链接EP作为测试集,观察到的网络ET作为训练集,未观察到的链接的集合为U-ET,链路预测问题是利用节点间相似性算法对AO中的任意节点对(x,y)计算一个相似度得分Sxy,所有的可能存在的边都被给予一个分数,对所有边的得分进行降序排序,得分最高的链接即为预测出的最可能遗失的链接,最后用测试集中的EP测试算法的预测精度.研究链路预测问题的核心是相似性指标的设计,因此本文将针对节点间的相似性指标进行研究.

3.2 一种基于共同邻居的全局节点遍历的链路预测算法

传统的CN指标仅考虑了节点间共同邻居的数目,虽然简单有效,但仅仅利用了共同邻居数目的信息,使得预测精度还有提升的空间.因此本文通过分析网络中存在的大度节点不利现象,并利用网络中的每个节点对待预测链接产生的贡献,提出了一个新的链路预测算法.

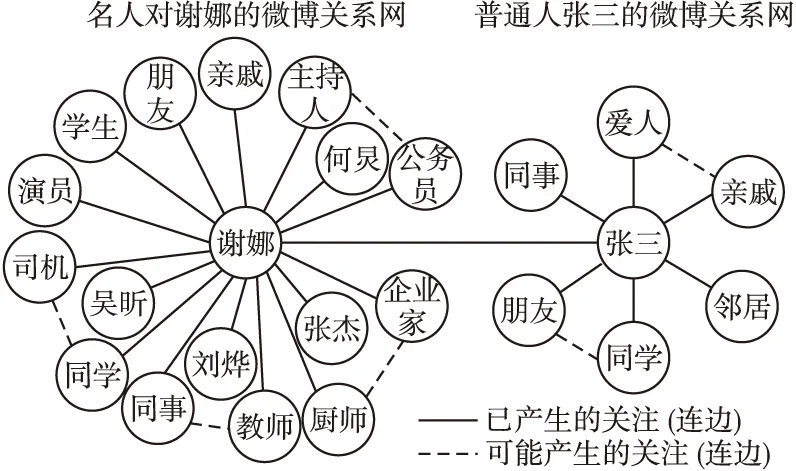
图2 新浪微博的关系网示意图Fig.2 Sina weibo network diagram

在新浪微博中,大家关注较多的是当红明星、各领域专家、网络红人,然而这些名人的粉丝之间产生关注的概率很小,称这种名人对于节点间产生链接的贡献很小的现象为大度节点不利现象.如图2所示是谢娜和普通人张三的微博关系网,在谢娜的新浪微博的8886万粉丝中,有她的亲戚朋友和同学同事,但是其中大部分粉丝都是因为崇拜才关注她的,这些粉丝来自全国各地各行各业,她的粉丝之间产生链接的概率就很小,例如她的粉丝中的学生和公务员之间几乎没有可能产生链接.相反,普通人张三的粉丝很少,关注他的人之间应该有一定的联系或者爱好,他的朋友和同学之间产生链接的概率就很高.很多网络中都存在这样的大度节点不利现象,在科学家合作网中引用著名学者的作者之间产生合作的概率就没有引用一般学者的作者之间产生合作的概率大.根据上述分析大度节点不利现象可以抽象为:

(7)

即两个节点x和y之间的相似度Sxy与节点的共同邻居的度kc成反比,δ为非零常数的反比例系数.为了减少两个节点之间的共同邻居的度kc的突出差异,降低共同邻居中的极小度节点和极大度节点对相似度的影响,所以利用节点之间的共同邻居的平均度的反比更能反映两个节点之间的相似度.由于数据在整个值域中不同区间的差异带来的影响不同,共同邻居度小的节点的差异敏感程度比度大的节点的差异敏感程度更高,因此对共同邻居的度kc取对数得到logkc,节点x和y之间的共同邻居的平均度MeanCN为:

(8)

结合上述分析的大度节点不利现象,节点x、y之间的相似度MZ定义为:

(9)

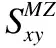
(10)

图3 网络拓扑结构示意图Fig.3 Network topology diagram

通过对比发现MZCN的相似性得分更高,主要由于其利用了同时与x,y节点有共同邻居的节点的影响,从而在理论上验证了该算法的优越性.综合分析上述影响节点之间相似性的因素,为了能够使链接预测算法在更多的网络上具有更高的预测精度,保留传统的CN指标在一些数据集上具有良好的预测精度的优点,在其基础上提出了一种基于共同邻居的全局节点遍历的链路预测算法(MZCN-CN),该指标定义为:

(11)

其中α、β是待定参数,需要根据实验所用的数据集进行试验确定,本文取σ=1.由于该指标中与两个参数相关的相似度在某一数据集上预测精度较高,而且这两项都是基于共同邻居的指标,它们之间可以通过加权相加的方法发挥各自的优势,使新的指标在各个数据集上都有着较高的预测精度.

本文将该指标用于链路预测算法,为了清晰描述该算法,给出了如下所示的算法1的伪代码:

算法1.一种改进共同邻居的节点遍历的链路预测算法

输入:给定一个含有V个节点和E条边的真实网络G(V,E);

输出:未知连边U-ET在MZCN-CN预测算法中的得分;

a) 将已存在连边按照9:1的比例随机划分训练集ET和测试集EP;

1 TrainNum = 0;

2 U=V(V-1)/2;

3 While(TrainNum<0.1*|E|)do

4 EP= Random selection from E;

5 TrainNum = TrainNum+1;

6 E=E-EP;

7 End;

8 ET=E;/*其余的已存在的连边作为训练集*/

b) 对未知连边U-ET利MZCN-CN指标进行相似性计算;

9 For z=1 to |U-ET| do

10 Edge(x,y)=select from edge(U-ET);

13 edge(U-ET)=edge(U-ET)-edge(x,y);

14 z=z+1;

15 End for z;

16 Output( The Score[z] of edge(U-ET) );

4 实验与分析

4.1 实验数据集

为了证明MZCN-CN指标的优越性以及确定指标中的各项参数,本文选取了来自6个不同领域的具有代表性的数据集进行实验,并与其他传统的预测指标作比较,选取的数据集分别为:a) 科学家合作网络(NS)[18]该网络是由发表过复杂网络为主题的论文作者构成.如果两个作者之间存在合作关系即在节点之间产生一条连边,其中节点代表作者.b) 政治博客网络(PB)[19]该网络的节点代表美国某政治论坛的博客网页,网络的连边的指网页之间存在超链接.c) 蛋白质相互作用网络(Yeast)[20]该网络中的蛋白质代表每个节点,蛋白质之间的相互作用关系表示节点之间的连边.d)线虫的神经网络(CE)[21]该网络中的线虫的神经元代表每个节点,神经元之间的链接代表网络中存在的边.e)食物链网络(FWFB)[22]该网络是由佛罗里达海湾雨季的食物链网络构成,其中节点代表各种生物以及捕食关系代表连边信息.f)路由器网络(Router)[23]该网络是由路由器代表的节点以及节点之间相连直接交换数据包的连边组成的Internet路由器层次网络.用于链路预测实验的6个真实网络的边以及节点等基本统计特性如表1所示.

表1 6个真实网络的基本统计特性
Table 1 Six basic statistical properties of real network

数据NMCrNS3799144．820．7986．04-0．082PB12221671427．360．362．74-0．221Yeast2375116939．850．3885．100．454CE297214814．470．3082．46-0．163FWFB128210632．4220．3551．776-0．112Router502262582．490．0336．45-0．138

其中N=|V|代表网络中存在的总的节点数,M=|E|代表网络中存在的总边数;代表网络的平均度,C代表网络集聚系数,其定义为一个节点的所有相邻节点之间的连边的数目占最大可能连边数目的比例;代表两个节点之间的平均最短距离.r(-1≤r≤1),代表网络连边两个端点度的相关系数(同配系数).

4.2 实验结果评价模型

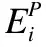
(12)

其中n′和n″的初始值都为0,因此AUC的定义为:

(13)

随机产生的所有连边的分数,AUC约等于0.5,因此AUC大于0.5的幅度体现算法比随机选择的方法的精确程度.

4.3 实验设计

本文利用MATLAB进行仿真实验,将上述的6个数据集分别按照9:1的比例随机划分训练集和测试集,然后利用AUC衡量新的指标在各个数据集上的预测精度.本文利用算法搜索MZCN-CN指标的两个α、β参数的最优解,并通过实验证明求解该参数的算法的可行性,然后通过实验证明该指标相比传统指标的优越性,具体如下所示.

4.3.1 确定α、β个参数的最优解及其可行性分析

为了使新指标在各个数据集都有较好的预测精度,需要解决两个参数的最优化问题,本文采用当β=1时,通过对α在[1,50]的取值范围内依次赋值并分别在6个数据集上进行试验得到对应的AUC,能够使大部分网络都具有较好的预测精度的α值即为最优解αmax,然后当α=αmax时,用同样的方法在[1,50]的范围内搜寻最优的βmax.当α=1时,经过在[1,50]范围内实验搜寻预测精度AUC最优的βmax2,通过对比βmax与βmax2的关系,证明该算法的可行性.

4.3.2 MZCN-CN指标的预测效果分析

将上述算法得到的βmax、βmax最优参数代入到MZCN-CN指标中,然后分别在6个数据集上对传统的CN、LHN、AA、RA、LNB-CN、LNB-RA以及MZCN-CN指标进行100次的随机独立实验,取100次独立实验预测精度AUC的平均值及其方差,最后与传统的预测指标的预测精度进行比较.

4.4 实验结果与分析

基于4.3节中的设计的实验内容进行实验,得到了如下所示的实验结果.

4.4.1 确定α、β两个参数的最优解及其可行性分析

当β=1时,随着自变量参数α在[1:1:50]范围内取不同值时,参数α=2附近6个数据集上的预测精度趋于稳定,为了确定最优值,缩小α的搜索空间为[1:0.1:3],MZCN-CN指标在6个数据集的预测精度AUC的变化曲线如图4所示:

从图中可以看出当α=2.1左右时,FWFB数据集的预测精度开始出现明显的下降,其余五个数据集的预测精度都达到了最好的预测精度而且以后都趋于稳定,所以本文选择参数α的最优解为αmax=2.1.

当α=αmax=2.1时,在6个数据集上的MZCN-CN指标随着参数β在[1:0.1:3]范围内变化的趋势如图5所示,由图可知,在β=1.4之前,MZCN-CN指标在FWFB和CE数据集的预测精度随着β的增加而不断增长,其他数据及的AUC也基本不变,CE数据集在β等于1.4左右时增长趋于平缓,而且1.4以后FWFB的预测精度也大体趋于稳定,所以选取参数βmax=1.4作为最优解.

图4 当β=1时,参数α与AUC的关系Fig.4 When β=1,the relationship between α and AUC

图5 当α=2.1时,参数β与AUC的关系Fig.5 When α=2.1,the relationship between β and AUC

为了证明该算法确定的参数是最优值,选择在α=1的情况下,分析各个数据集的预测精度随着β的变化情况来确定最优的βmax,其变化曲线如图6所示,从图中可以看出当β≈1.4附近时,FWFB数据集取得最高的预测精度的同时其他数据集的预测精度也基本不变.因此取β的最优解为βmax1=1.4,与在α=αmax=2.1的情况下确定的βmax2=1.4对比发现βmax1≈βmax2=1.4;从而证明了该算法的可行性,得到了指标中各个参数的最优解,而且有效避免了全局搜索,降低了算法的复杂度.

图6 当α=1时,参数β与AUC的关系Fig.6 When α=1,the relationship between β and AUC

在α=2.1、β=1.4时该指标在各个数据集上都具有较高的预测精度,因此本文提出MZCN-CN的指标定义为:

(14)

4.4.2 MZCN-CN指标的预测效果分析

传统的CN、LHN、AA、RA、LNB-CN、LNB-RA指标以及MZCN-CN指标在NS、PB、Yeast、CE、FWFB、Router 6个数据集上的预测精度AUC的评价结果如表2所示,而且100次独立实验的AUC方差都稳定在0.0001以内,说明随机抽样的结果具有可靠性.

表2 不同链路预测算法的AUC评价结果
Table 2 AUC results of different link prediction algorithm

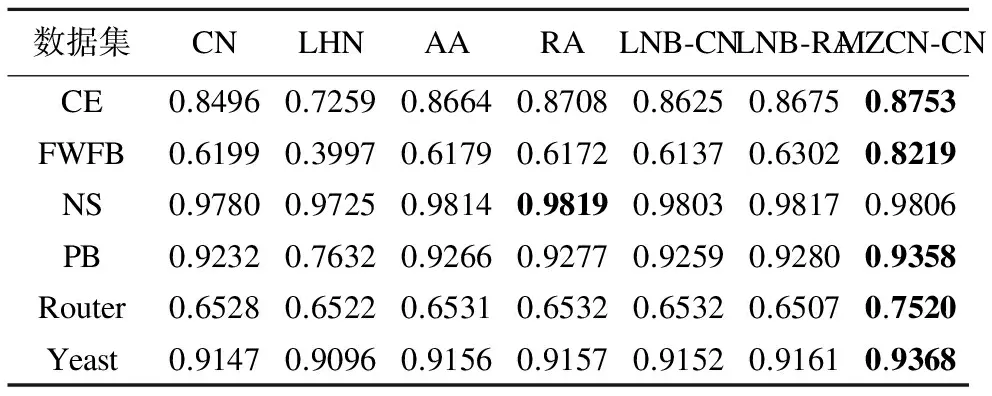
数据集CNLHNAARALNB⁃CNLNB⁃RAMZCN⁃CNCE0．84960．72590．86640．87080．86250．86750．8753FWFB0．61990．39970．61790．61720．61370．63020．8219NS0．97800．97250．98140．98190．98030．98170．9806PB0．92320．76320．92660．92770．92590．92800．9358Router0．65280．65220．65310．65320．65320．65070．7520Yeast0．91470．90960．91560．91570．91520．91610．9368

从表2中可以看出,本文提出的MZCN-CN指标相比传统的预测指标在五个数据集上都具有最高的预测精度,在各个数据集上的预测精度都有显著提升.只有在NS网络上表现不是最好,但相比最优的RA指标也只相差0.0013,而且在FWFB数据集上的预测精度较传统最好的指标AUC提高了约20%,在Router数据集上预测精度提高了10%.结合这两个网络的统计特性进行分析可知,FWFB的网络平均度最大,其仅有128个节点但其平均度达到了32,说明大度节点较多,MZCN-CN指标的大度节点不利作用起到了效果,同时其平均最短距离最小、簇系数较大具有小世界效应,说明该指标对具有小世界效应的网络也有较好的预测效果.Router网络拥有5022个节点的平均度仅为2.49,说明网络中大度节点较少,所以MZCN-CN指标对其精度的提高仅为10%,该网络的集聚系数较小,仅为0.033,该由于共同邻居指标对于集聚系数较低的网络预测精度较差,而MZCN-CN指标对其预测精度却有了提高,在一定程度上克服了集聚系数小对于预测精度的影响,证明该指标的预测精度的优越性,而且计算复杂度较低,适用于大规模的网络.

通过对CN、LHN、AA、RA、LNB-CN、LNB-RA以及MZCN-CN 7个指标分别在NS、PB、Yeast、CE、FWFB、Router六个数据集上进行100次独立实验的AUC取平均值后的分布情况如图7所示,该图表示各个指标的整体性能,可以看出MZCN-CN指标在各个真实网络中的预测精度都高于其他传统的预测指标,说明了该指标预测精度的优越性以及其较强的普适性,尤其在FWFB网络和Router网络上预测精度表现较为突出,而且该指标的计算复杂度较低,因此本文提出的算法可以适用于大部分的网络,应用前景广阔.

5 总 结

本文针对传统链路预测中没有全面考虑影响节点间相似性的因素、网络中的大度节点不利现象,在基于共同邻居指标的基础上,通过对网络中大度节点不利现象的分析,在定义了大度节点对于节点间产生链接的作用的同时,综合考虑了网络中每个节点对于待测节点间产生链接的贡献,综合传统指标的优势,提出了MZCN-CN指标,并通过实验确定新指标的各项参数,使其具有最好的预测效果,该指标通过在6个真实网络与6个传统的预测指标对比AUC结果证明该指标的预测精度高,具有普适性强的优势.

图7 各个指标的整体性能Fig.7 Overall performance of each indicator

今后的研究重点是针对该指标进一步优化,通过引入优化算法,将其预测精度进一步提升,使其在更多的网络上都表现出较好的预测精度,以及研究该指标如何应用到加权或有向网络中.

[1] Lv Lin-yuan,Zhou Tao.Link prediction in complex networks:a survey [J].Physica A Statistical Mechanics & Its Applications,2011,390(6):1150-1170.

[2] Pan Li-ming,Zhou Tao,Lv Lin-yuan,et al.Predicting missing links and identifying spurious links via likelihood analysis [J].Scientific Reports,2016,6(22955):1-24.

[3] Chuang Ma,Zhou Tao,Zhang Hai-feng.Playing the role of weak clique property in link prediction:A friend recommendation model[J].Scientific Reports,2016,6(30098):1-12.

[4] Yu Hai-yuan,Braun Pascal,Yildirim,et al.High-quality binary protein interaction map of the yeast interactome network [J].Science,2008,322(5898):104-110.

[5] Carlo Vittorio-cannistraci,Gregorio Alanis-lobato,Timothy Ravasi.From link-prediction in brain connectomes and protein interactomes to the local-community-paradigm in complex networks [J].Scientific Reports,2015,3(4):1613-1613.

[6] Lv Lin-yuan,Medo Matúš,Chi Ho-yeung,et al.Recommender systems [J].Physics Reports,2012,519(1):1-49.

[7] Guimerà Roger,Marta Sales-pardo,Stanley H E.Missing and spurious interactions and the reconstruction of complex networks [J].Proceedings of the National Academy of Sciences,2009,106(52):22073-22078.

[8] Mark Newman.Clustering and preferential attachment in growing networks [J].Physical Review E Statistical Nonlinear & Soft Matter Physics,2001,64(025102):1-4.

[9] Elizabeth Leich,Petter Holme,Mark Newman.Vertex similarity in networks [J].Physical Review E Statistical Nonlinear & Soft Matter Physics,2006,73(026120):1-10.

[10] Adamic Lada A,Adar Eytan.Friends and neighbors on the Web [J].Social Networks,2003,25(3):211-230.

[11] Lv Lin-yuan,Jin Ci-hang,Zhou Tao.Similarity index based on local paths for link prediction of complex networks [J].Physical Review E Statistical Nonlinear & Soft Matter Physics,2009,80(2):593-598.

[12] Barabasi Albert-laszlo,Albert Reka.Emergence of scaling in random networks [J].Science,1999,286(5439):509-512.

[13] Zhou Tao,Lv Lin-yuan,Zhang Yi-cheng.Predicting missing links via local information [J].The European Physical Journal B,2009,71(4):623-630.

[14] Katz Leo.A new status index derived from sociometric analysis [J].Psychometrika,1953,18(1):39-43.

[15] Liu Zhen,Zhang Qian-ming,Lv Lin-yuan,et al.Link prediction in complex networks:a local naïve Bayes model [J].Europhysics Letters,2011,96(48007):1-6.

[16] Liu Da-wei,Lv Yuan-na,Yu Zhi-hua.An improved link prediction algorithm for complex networks [J].Journal of Chinese Computer Systems,2016,37(5):1071-1074.

[17] Zeng Shan.Link prediction based on local information considering preferential attachment[J].Physica A Statistical Mechanics & Its Applications,2016,443:537-542.

[18] Newman M E J.Finding community structure in networks using the eigenvectors of matrices[J].Physical Review E Statistical Nonlinear & Soft Matter Physics,2006,74(3):92-100.

[19] Adamic L A,Glance N.The political blogosphere and the 2004 U.S.election:divided they blog[C].International Workshop on Link Discovery,ACM,2005:36-43.

[20] Von Mering C,Krause R,Snel B,et al.Comparative assessment of large-scale data sets of protein-protein interactions [J].Nature,2002,417(6887):399-403.

[21] Watts Duncan james,Strogatz Steven H.Collective dynamics of ′small-world′ networks [C].Nature,1998:440-442.

[22] Ulanowicz Robert,Heymans Johanna,Egnotovich.Network analysis of trophic dynamics in south florida ecosystems[J].FY 99:The Graminoid Ecosystem,2000,22(5):112-123.

[23] Spring Neil,Mahajan Ratul,Wetherall David.Measuring ISP topologies with rocketfuel [J].Acm Sigcomm Computer Communication Review,2002,32(4):133-145.

[24] Hanley J A,Mcneil B J.The meaning and use of the area under a receiver operating characteristic (ROC) curve [J].Radiology,1982,143(1):29-36.

附中文参考文献：

[16] 刘大伟,吕元娜,余智华.一种改进的复杂网络链路预测算法[J].小型微型计算机系统,2016,37(5):1071-1074.