无线传感网多多项式密钥分配方案研究

王行甫,吴立涛,苗付友

(中国科学技术大学 计算机科学与技术学院,合肥 230027)

1 引 言

随着无线通信技术和传感器技术的快速发展,无线传感器网络(Wireless Sensor Networks,WSNs)在军事和民用方面得到了广泛的应用.WSNs是由大量的具有无线通信能力的、低功耗、低成本传感器节点组成的网络,节点一般具有有限的计算能力,有限的存储空间,有限的能量,被部署在人类无法长期生存或者人类生存成本过高的区域,用于监控、检测的用途,如军事检测、森林火灾监测[1]、地震监控等领域.

由于传感器节点部署范围广,通常处于无人值守的状态,在某些应用中传感器监控的数据比较敏感,导致传感器的安全性需要极大的重视.且WSNs的特殊性使得其面临很多安全问题,如1)传感器通常使用无线通信的方式进行数据交换,而无线通信的方式很容易使得数据被恶意节点监听、捕获.2)sink节点是用来汇聚传感器数据的节点,由于传感器节点能量有限,而节点一旦部署,就很难再更换能量源,因此移动sink节点的路由算法被众多研究者所青睐.但是由于sink节点的不固定,导致恶意节点可以仿冒sink节点,对传感器网络进行攻击.

为了解决以上两个典型的安全问题,加密方案被引入WSNs设计中.在加密过程中,密钥协商是一个非常重要的步骤,它关系着加密过程是否可靠,加密结果是否有效,如果密钥发生泄露,那么加密就变成了无用功.根据文献[2]所述在通用网络中,密钥协商一般有三种研究方案,分别是1)可信服务器方案,这种方案依赖于一个可相信的服务器,服务器起着中间协商的作用,两个需要进行密钥协商的节点分别与可信服务器进行通信,由服务器分发一个共享密钥进行加密通信.文献[3]设计的Kerberos方案采用了这样的方案,但是在WSNs中,节点受到通信距离的限制,导致这种方案无法实现.2)公钥密码体系方案,这种方案依赖于非对称加密算法,受限于节点的计算能力和在WSNs中可能不存在的公钥基础设施,这种方案在WSNs中也无法实现.3)密钥预分配方案,这种方案在节点部署之前就将密钥配置到节点中,从方案设计和实验结果来看,是最适合于WSNs的,也是研究者研究的最多的一种方案.本文拟提出的密钥分配方案也是基于此设计的.

本文的全文安排如下,在第2章节介绍在密钥分配方案设计中的相关工作,并对方案的优点和不足提出本文的观点.在第3章节介绍本文提出的基于多项式的密钥分配方案设计,并对其进行分析.在第4章节介绍本文提出的分配方案的实验结果,并对实验结果进行分析.第5章节是对本文工作的总结.

2 相关工作

在已有的密钥预分配方案设计中,主要基于两种设计方法,1)基于密钥池的密钥预分配方案;2)基于多项式的密钥预分配方案.

2.1 基于密钥池的密钥预分配方案

密钥池预分配方案是在节点部署前,由服务器生成大量的密钥,节点被随机分配部分密钥,然后进行部署.在密钥协商阶段,两个节点寻找是否具有公共密钥,如果有,则使用公共密钥作为两个节点通信的密钥,否则不能建立通信.文献[4]提出的E-G方案是一种基于概率性的随机密钥分配方案,该方案首先在节点部署前随机分配密钥,这样节点间以一定概率拥有相同密钥,在协商阶段查看是否有相同密钥,如果存在,则将该密钥作为通信加密的密钥,否则寻找中间节点来帮助两个节点建立通信.该方案虽然基于一定的随机性分配密钥,但是由于在密钥协商阶段只需要找到一个相同的密钥即可建立连接,使得节点的抗捕获性较弱.文献[5]针对E-G方案的不足,提出了q-composite方案(q-composite key predistribution scheme),该方案需要任意两个节点至少存在q个共享密钥时,节点才会协商会话密钥K=Hash(k1‖k2‖…‖kq).不难看出,E-G方案是q-composite方案在q=1时的特殊情况,增大q值可以提高节点的抗捕获性,提升系统安全性,但是节点间难以寻找到足够的密钥,导致节点连通性降低.

2.2 基于多项式的密钥预分配方案

多项式预分配方案通常是基于某种数学理论建立的,和密钥池预分配方案相比,它具有网络安全性高、通信和存储负载小等优点[6].比较经典的多项式密钥预分配方案主要是Blom方案[7]和Blundo方案[8].Blom方案是基于对称矩阵建立两节点间的共享密钥,在部署节点前在服务器生成一个基于有限域GF(q)的(λ+1)×N的公共信息矩阵G和(λ+1)×(λ+1)的秘密对称矩阵D,然后由公式获得一个Blom矩阵A,将矩阵A的一行和矩阵G的一列作为密钥存储在每个节点中.节点在密钥协商过程中,分别将各自内存中的种子密钥发送给对方,两节点分别计算密钥,由于矩阵是对称的,两节点计算得到的密钥一定相同,此密钥可以作为节点的会话密钥.该方案存储的密钥信息较少,占用内存较少,同时因为传感器建立会话的密钥是不相关的,所以节点抗捕获性较强,该方案不足的地方在于存在严重的门限λ问题.Blundo方案是基于Blom方案的设计,不过Blundo方案使用的是二元t次对称多项式函数,在有限域GF(q)上生成一个二元t次对称多项式,在节点部署前将多项式保存在节点中,在密钥协商过程中,两个节点交换彼此的身份ID来计算通信密钥,由于多项式是对称的,节点计算结果一定是相同的.Blundo方案每个节点仅需要存储多项式函数的t+1个系数即可,占用内存少,计算代价低.该方案的不足之处在于存在“t-secure”问题[9].

3 多多项式密钥分配方案

由于密钥池分配方案的基本原理是节点各自保存密钥池的一个子集,在密钥协商的过程中,寻找两个节点保存的子集密钥的交集,如果交集为空,则这两个节点没有协商出一致的密钥,无法建立连接,如果交集不为空,则使用交集中的密钥作为两个节点通信的加密密钥,因而密钥池分配方案无法确保网络中的节点一定能建立连通[10].当被捕获的节点达到一定数量的时候,将这些被捕获节点的密钥合并在一起,就可以得到一个很大的密钥池子集,利用这个大子集可以与网络中的其他大部分节点进行合法的通信,造成密钥空间泄露.基于多项式的密钥分配方案存在“t-secure”问题,一旦存在个t+1节点泄露,由于只有单一多项式,如果输入一定,则输出也是一定的.攻击者可以利用一定的输入获得t+1个密钥,进而构建一个至少含有t+1个方程的方程组,使得用于计算密钥的多项式函数的所有系数被计算出来,导致密钥完全泄露.本文拟提出的多多项式密钥分配方案(Multi-PolynomialsKey Distribution Scheme,MPKDS)就是为了解决上述问题,节点在密钥协商阶段,利用各自获得的参数,基于多项式的计算,获得用于加密通信的密钥,进行安全通信,实现100%的连通性.节点间通信密钥独立,即使某一密钥被窃取也不存在密钥空间被泄露的问题,因为使用多个多项式,攻击者几乎不可能构建正确的t+1方程组,解方程求得多项式系数,即不存在“t-secure”问题.

3.1 密钥分配步骤

MPKDS采用的也是基于对称二元t次多项式函数的方案,下面是密钥分配方案具体步骤.

1)选择二元t次对称多项式作为密钥生成函数,选择二元对称多项式的原因在于为了保证两个节点各自控制一个参数,同时计算结果一致.在节点部署前,由服务器端在有限域GF(q)随机生成n个二元t次对称多项式函数,其表达式如下:

(1)

2)每个节点都分配n个完全相同的多项式,按照无线传感器网络构建规则,可以进行随机部署.在网络运行过程中,任意两个节点想要建立会话,必须先要进行密钥协商,得到一致的密钥后,说明节点是可信的,认证成功.接下来的通信过程都要使用该密钥进行加密,保证网络通信的安全性.

3)密钥协商阶段,两个节点首先在节点内各自生成一个随机数,发送到对方节点中,这样每个节点可以得到两个随机数,作为节点内存储的n个多项式的参数,生成n个基于二元t次多项式的密钥,

由于f(x,y)是二元对称多项式函数，有

f(x,y)=f(y,x)

(2)

所以每个节点在得到两个随机数后,生成的密钥是一致的.这些密钥组成密钥空间N.密钥空间N中的密钥作为发送数据时用于加密的密钥,接下来的工作是如何和通信对方节点商量使用一致的密钥.

4)密钥空间N中的n个密钥，对于每一个密钥，都使用密钥空间中的n个密钥进行加密，得到另外一个密钥空间M，密钥空间M的大小记为|M|=n×n=n2，其中每n个空间M中的密钥可以映射到空间N中的一个密钥.

5)节点在通信的时候,首先随机选择密钥空间N中任意一个密钥对通信数据进行加密,假设这里使用的是密钥a,在密钥空间M中存在n个密钥可以映射为密钥a,从这n中任意选择一个密钥,假设这里使用的是密钥b,添加到数据包包头,作为对方节点计算密钥a的参数,这样,数据包的形式可以使用下面的表达式表示:

p={b+F(a,d)|a∈M,b∈N,f(b)→a}

(3)

在上述表达式中,函数F是加密函数,函数f是单向映射函数.表达式p的形式可以理解为,首先任意选择密钥空间M中的密钥a对数据d进行加密,存在密钥空间N,N中的任意密钥可以映射为M中的密钥,现选择N中的密钥b,密钥b可以映射为M中的密钥a,将密钥b作为数据包前导数据发送到对方节点.对方节点在收到数据包后,首先从数据包中分离出b，将b映射到密钥空间N中的密钥a，使用a对数据包中的数据进行解密，得到正确的明文数据.

3.2 MPKDS分析

3.2.1 连通性分析

与密钥池方案不同的是,基于多项式的方案所有节点在部署前都会被分配相同的多项式函数.在本方案中,所有节点会被分配由服务器生成的n个多项式,在密钥商议阶段使用随机数作为多项式的参数,计算得到密钥空间N,再对密钥空间N进行加密得到密钥空间M,所有的计算结果都是确定的,节点虽然是单独计算,但是基于二元对称多项式的特性,计算结果是确定一致的.在密钥商议阶段一定可以计算得到一致的密钥作为会话密钥,所以本方案的连通性是100%,网络内任意两个合法节点都可以建立通信.

3.2.2 安全性分析

当网络中被捕获的节点数量较少时,无论是基于密钥池的分配方案,还是基于多项式的分配方案都可以很好的保证网络的安全性.但是一旦捕获数量多,密钥池分配方案会面临密钥空间被泄露,导致网络安全性被破坏.单一多项式的分配方案面临很严重的“t-secure”问题,本文提出的多多项式分配方案,由于每次使用的都是密钥空间N的随机密钥,密钥之间相互独立,随着多项式个数n的增大,密钥空间大小快速增长,保证了网络空间的安全性.

基于多项式的分配方案,节点在每次通信时都要计算新的密钥,而不是使用密钥池方案中的固定密钥.攻击者如果想要破解网络,只有计算出所有多项式的系数,得到完整的多项式函数方可.为了验证方案的安全性,假设恶意节点可以任意获取节点间通信的数据包,n个二元t次多项式共有系数个,如果要解得所有系数,需要构建个方程组,因为每次节点通信都是从n个密钥中随机选择任意一个密钥,为了获取经过所有密钥加密的数据包,使用概率统计的方法,恶意节点需要获取数据包个数的期望为Pc

(4)

多多项式密钥分配方案伪代码

密钥协商阶段：

r1=generate_one_random_integer()

r2=receive_one_random_integer()

key_space_N=[]

for f in polynomials_pool:

key_space_N.append(f(rl,r2))

key_space_M={}

key_space_map={}

for key_n in key_space_N:

key_space_M[key_n]=[]

for key_m in key_space_N:

key_space_M[key_n].append(crypt(key_m,key_n)) # for crypt

key_space_map[key_m]=key_n # decrypt

发送数据阶段：

key=random_get_key_from(key_space_N)

random_key=random_get_key_from(key_space_M[key])

package_data=crypt(key,data)

package=[random_key,package_data]

send(package)

接收数据阶段：

package=get_package()

rand_key=get_random_key(package)

key=key_space_map[random_key]

crypt_data=get_data(package)

data=decrypt(key,crypt_data)

图1表示了在n个二元t次多项式组成的密钥空间中,获取经过所有密钥加密的数据包,至少需要得到的数据包的个数Pc与n和t的关系.从图中可以看到,即使n和t缓慢增长,Pc的增长速度非常快,因此攻击者想要获取足够多有效的数据包难度大大增大,有效提升了网络的安全性.

假设恶意节点得到经过所有密钥加密的数据包，为了解出所有多项式的系数，需要构建n×(t+1)个方程组.现在假设攻击者得到了Pc个有效数据包，从其中选择任意n×(t+1)个数用来构建方程组，由于节点随机选择密钥的原因，这里Pc应该远远大于n×(t+1)，因为节点可能多次选择了相同的密钥进行加密a进行加密，但是不同的密钥b作为数据包前导数据.根据排列组合的知识共有Pn种不同的方程组

(5)

因此构建正确的方程组,得到全部正确的多项式系数为的概率P为

(6)

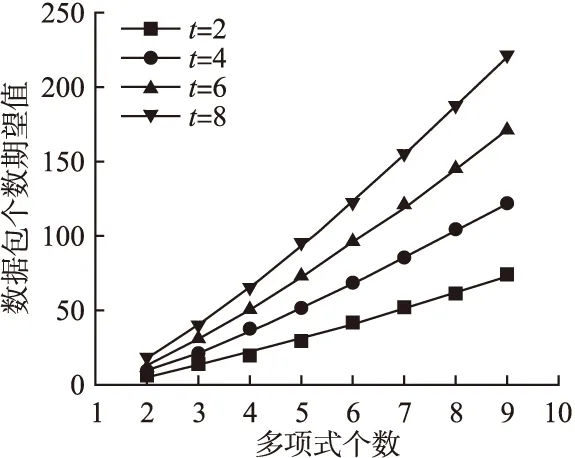
图1 捕获有效数据包期望与t、n的关系Fig.1 Relationship between the expectation of valid captured packets and t and n

表1记录的数据是随着n和t的增长,Pn的变化情况,从表中可以看到,Pn的快速增长使得构建正确方程组的概率几乎为0,有效保证了该密钥分配方案的安全性.

表1 Pn和t、n变化的关系表
Table 1 Relationship between Pnand the variations of t and n.

nt=2t=4t=6t=827．2e+23．6e+68．7e+106．4e+1532．6e+82．2e+172．3e+271．3e+3843．1e+141．8e+286e+432．1e+6053．9e+207．4e+394．4e+609．3e+8261．3e+274．7e+512．4e+787．1e+10675．8e+339．3e+637．9e+962．3e+13186e+405e+764．9e+1153e+15698．1e+476．8e+899．4e+1342．4e+182

4 实验性能分析

无线传感器网络节点最重要的资源就是计算能力、存储能力和能耗问题.由于影响能耗问题的因素诸多,密钥分配方案不是根本原因,本文主要在计算能力和存储能力两个方面将MPKDS与Blundo方案进行对比分析.如今在嵌入式领域使用最广泛的处理器即ARM公司设计的ARM内核CPU,本文基于ARM CortexM3架构的CPU指令集,系统时钟120MHz,进行资源统计.通过统计程序运行时间作为占用计算资源的评价标准,在ARM架构下缺乏精确的内存占用统计工具,本文通过分析反汇编程序,统计占用的寄存器、内存空间作为占用存储能力的评价标准.

表2 MPKDS与Blundo比较结果表(t=4)
Table 2 Comparison results between MPKDS and Blundo(t=4)

算法建立时间(ms)内存占用(Byte)Blundo123928MPKDS(n=1)128960MPKDS(n=2)1531412MPKDS(n=3)1841988MPKDS(n=4)2412428MPKDS(n=5)2982996MPKDS(n=6)3553508MPKDS(n=7)4134116

由表2分析知，MPKDS对节点占用资源总体上处于线性增长的趋势.当n=1时，MPKDS方案就退化为Blundo方案；1

5 结束语

现有的密钥分配方案中,基于密钥池分配的方案存在占用内存过大、抗捕获性不强、概率连通等不足,常规基于多项式的分配方案虽然占用内存小,但是存在严重的“t-secure”问题,本文针对上述不足,提出的基于多多项式的密钥分配方案,保证网络节点的100%连通性,避免了“t-secure”问题,增强网络节点的抗捕获性,网络的安全性.实验表明,MPKDS对节点计算能力要求不高,使用合适的多项式个数参数,可以在存储资源有限的情况下极大的保证了网络的安全性.

[1] Grammalidis N,Cetin E,Dimitropoulos K,et al.A multi-sensor network for the protection of cultural heritage[C].Signal Processing Conference,2011 19th European.IEEE,2011:889-893.

[2] Du Wen-liang,Deng Jing-han,Yunghsiang S,et al.A pairwise key predistribution scheme for wireless sensor networks[J].ACM Transactions on Information and System Security(TISSEC),2005,8(2):228-258.

[3] Clifford Neuman B,Theodore Ts′o.Kerberos:an authentication service for computer networks[J].IEEE Communications Magazine,1994,32(9):33-38.

[4] Laurent Eschenauer,Virgil D.Gligor.A key-management scheme for distributed aensor networks[C].Processding of the 9th ACM Conference on Computer and Communications Security,2002:41-47.

[5] Haowen Chan,Perrig A,song D.Random key predistribution schemes for sensor networks[C].Security and Privacy,Proceedings,2003 Symposium on.IEEE,2003:197-213.

[6] Saahira Banu Ahmed,Ananthi Shesasayee.To enhance security in wireless sensor networks with mobile sink[C].Current Trends in Engineering and Technology(ICCTET),2014 2nd International Conference on.IEEE,2014:547-550.

[7] Rolf Blom.An optimal class of symmetric key generation systems[C].Workshop on the Theory and Application of Cryptographic Techniques.Springer Berlin Heidelberg,1984:335-338.

[8] Blundo C,De Santis A,Herzberg A,et al.Perfectly-secure key distribution for dynamic conferences[C].Annual International Cryptology Conference.Springer Berlin Heidelberg,1992:471-486.

[9] Chen Yan,Wu Wen-kang,Liang Jun-bin.High safety scheme of key pre-distribution with a mobile sink in wireless sensor network[J].Journal of Guangxi Normal Universite:Natural Science Edition,2013,31(3):164-168.

[10] Liao Dong-ping.A key management research based on polynomial for WSN[D].Changsha:Central South University,2014.

附中文参考文献：

[9] 陈 燕,吴文康,梁俊斌.Sink移动无线传感网中高安全性密钥预分配方案[J].广西师范大学学报(自然科学版),2013,31(3):164-168.

[10] 廖东平.基于多项式的WSN密钥管理方案研究[D].长沙:中南大学,2014.