基于逆矩阵法的汽车关键点振动传递路径分析

, ,，,

(1.上海工程技术大学 汽车工程学院,上海 201620; 2.广州汽车集团股份有限公司 汽车工程研究院,广州 )

0 引言

汽车作为一个复杂的系统，往往受到多种振动和噪声源的激励。诸如方向盘、座椅、动力系统等部位的振动直接影响驾驶舒适性和平顺性，可以将这些部位看作是汽车振动的关键点，为了研究这些关键点之间的振动传递关系，对这些关键点进行载荷识别、传递路径分析(TPA)和路径贡献量分析非常有必要。

传递路径分析可以快速准确分辨出目标点位置NVH(noise, vibration and harness)问题的影响根源[1]。早先，Vecchio[2]等人针对混合动力公交车应用传递路径法对噪声和振动源进行了载荷识别，并且测试激励源与目标点的传递函数，预测了车内NVH水平。Schuhmacher[3]等人通过体积声源和激振器激励车身，研究了时域传递路径分析方法在结构噪声和空气噪声识别和路径贡献量分析中的应用。Tandogan[4]等测试并分析了车内结构路径和空气路径的噪声源及其噪声传递函数，对比了车内噪声的预测与测试结果。Zheng[5]等将工况传递路径法扩展到时域，研究多个运动声源的瞬态特性及其贡献量，并对某重型卡车的通过噪声的声源贡献量进行了分析。同济大学的慕乐和周鋐等[6]针对某商用车怠速时转向盘振动问题进行研究，建立了传递路径模型，基于该模型进行主要贡献路径识别。侯锁军等[7]针对某国产样车存在的怠速时方向盘抖动的问题，采用传递路径分析方法寻找定位方向盘抖动的具体原因。可见，依据传递路径分析的结果可以诊断出并有针对性地改善或者解决NVH问题。

对汽车关键点振动进行传递路径分析时，激励点的载荷识别是一项重要工作，是对各传递路径贡献量分析的前提。激励点载荷识别方法有直接法和间接法[8]。直接法就是用力传感器在激励点位置直接测量载荷力的大小；而间接法则是通过计算的方法间接得到激励点载荷。载荷识别的间接方法主要有悬置刚度法和逆矩阵法。Melo[9]等对比了分别应用载荷力直接测试法和逆矩阵法的传递路径分析结果，结果表明两种方法可获得同样的路径贡献量结果。但是直接测试法过程安装力传感器极为不方便。Padilha[10]等对比研究了悬置刚度法和逆矩阵法，发现在移除振动或者噪声源时，悬置刚度法识别的结构更为精确，源存在的情况下逆矩阵法更为可取。Dom[11]等研究了悬置刚度法和逆矩阵法预测激励点载荷的效果，提出使用采用运行工况法弥补预测中的缺陷。MaartenV[12]等人也指出了用直接测试获得载荷存在缺乏安装空间和不能测量到全部的自由度的弊端。虽然传递路径分析中使用逆矩阵法识别载荷的过程中往往需要大量的测试，存在矩阵病态问题，但是相比较于悬置刚度法，不用测试弹性元件的动刚度，测试过程中受空间约束较小。除此之外，逆矩阵法由于考虑各个路径之间的耦合，且对于非方阵存在的病态问题可使用奇异值分解求得载荷识别方程的最小二乘解[13]，载荷识别的精度较高。

因此，本文采用矩阵求逆识别激励点载荷力，引入参考点工况响应数据，对实际的传递函数矩阵进行构建，完成激励点载荷力的识别，对识别的载荷进行验证并将识别的载荷用于各条路径对目标点的贡献量分析，找到振动传递的关键路径，对关键路径进行载荷力和传递函数分析，判断振动产生的原因是激励点载荷过大的原因还是结构传递函数的原因，为针对性的提出改进措施提供依据。

1 基本理论

1.1 传递函数逆矩阵

系统在外界激励作用下会产生一定的响应，在激振力f(t)的作用下，系统的运动微分方程为：

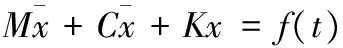
(1)

式中，M、C和K分别表示系统的质量矩阵、阻尼矩阵和刚度矩阵，对运动微分方程进行快速傅里叶变换，在频域中可以得到：

(2)

式中，H(ω)即为频率响应函数(FRF)或称为系统的传递函数。传递函数是系统的一种固有特性，它可以表征系统在受到单位激励后沿着某一条传递路径在某处产生振动的大小[14]。根据式(2)，如果已知系统的传递函数，就可以通过输入信号求出输出信号，反之，也可通过输出信号求出输入信号。

对线性系统，当有激励力F1、F2、F3,…,Fn时，系统存在响应X1、X2、X3,…,Xm，由系统的运动方程可得：

(3)

式中，Hmn为激励点Fn到响应点Xm的传递函数。

式(3)两边同乘以传递函数逆矩阵可得载荷力计算公式：

(4)

由式(4)可知，激励点载荷力等于激励点到响应点组成的传递函数逆矩阵与响应信号相乘得到。为得到激励点载荷力只需测得传递函数并构建传递函数矩阵，对矩阵进行求逆计算。但往往传递函数矩阵不是方阵的形式，无法直接求其逆矩阵，可使用奇异值分解求得载荷识别方程(4)的最小二乘解。

1.2 传递路径分析

传递路径分析法是研究系统的传递特性，假设汽车是线性时不变系统，车内目标点的振动大小等于车身各个激励点的载荷通过不同的路径传递到目标点的振动的叠加[15]。激励点的每一个自由度到目标点均形成一条传递路径，通常只考虑X,Y和Z向3个方向平动自由度。如果已知激励点i上的载荷和激励点i到目标点t的传递函数，则n条路径上激励点对目标点位置振动贡献量可以表示为[16]：

(5)

式中，Tit为激励点i到目标点t的贡献响应，可以是加速度信号或者力信号。Fi为路径点i的载荷，分析振动载荷时一般为载荷力，由传递函数逆矩阵法(4)计算得出。

根据式(4)和(5)可得目标点贡献量计算矩阵：

(6)

2 关键点振动传递路径模型的建立

方向盘和座椅导轨的振动激励来自发动机以及排气系统，两者分别通过发动机前后悬置和排气管前后悬挂点与车身连接。因此在建模的过程中，考虑发动机悬置点和排气管悬挂点作为激励点，通过不同的路径把振动传递到方向盘和座椅导轨处。发动机前后两个悬置点和排气管前后悬挂处的传递路径，每个激励点有X,Y和Z三个方向,共有4×3=12条路径。

2.1 分析模型的建立

2.1.1 坐标系的选定

选定汽车前进方向的方向为整车坐标的正X方向；汽车前进左手方向为整车坐标的正Y方向；垂直向上作为整车坐标的正Z方向。测试过程中传感器布置方向与整车坐标统一。

2.1.2 关键点的定义

汽车方向盘、座椅、动力系统等部位的振动直接影响驾驶员的驾驶舒适性和乘客的乘坐舒适性，这些部位的振动可以用一些关键点的振动来衡量。因此，将车内振动的目标点、激励点和参考点统统定义为汽车振动的关键点。本文选取的目标点位置为方向盘十二点X、Y、Z三个方向和座椅导轨X、Y、Z三个方向。激励点的位置为发动机前后悬置点与车身的连接点X、Y、Z三个方向和排气管与车身前后的悬挂点X、Y、Z三个方向。

参考点的位置选择激励点附近，要求参考信号的数目是激励点数目的2倍及以上[17]，在每个激励点附近选择两个参考点，共8个参考点。表1为关键点的位置及名称，测试过程中在每个关键点位置均布置加速度传感器。

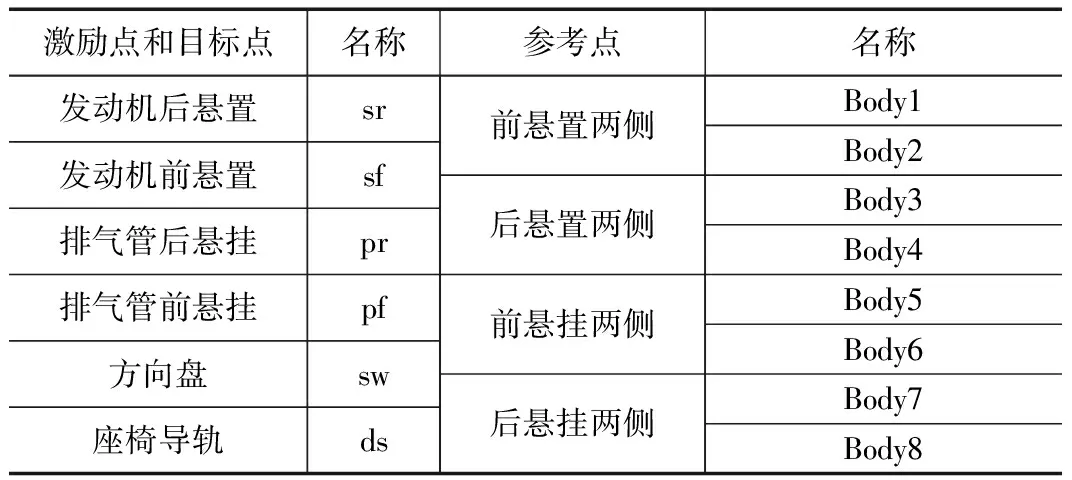
表1 技术指标及测试要求关键点位置及名称

2.2 计算模型的建立

2.2.1 激励点载荷的计算

表2 激励点的载荷和参考点响应

根据定义的关键点和公式(3)，构建激励点载荷计算的传递函数矩阵：

(7)

式中,Fij表示第i激励点j方向的载荷(i=sf,sr…pr;j=X,Y,Z)

Anj表示第n个参考点j方向加速度信号(n=1,2…8;j=X,Y,Z)

由公式(7)传递函数矩阵求逆矩阵，对激励点载荷进行识别：

(8)

2.2.2 目标点贡献量的计算

由公式(6)目标点贡献量计算矩阵可以得到各条路径在目标点各个方向的贡献量：

(9)

式中,TswZ,TdsZ分别表示方向盘和座椅导轨Z向的贡献量。

2.3 关键点振动传递路径试验

根据公式(7)可知，试验包括两个部分，采集传递函数和工况响应数据，试验设备包括计算机、LMS数据采集前端、力锤、三向加速度传感器、转速传感器。图1为试验设备和部分传感器布置。

图1 试验设备和传感器布置

2.3.1 传递函数的获取

传递函数的获取方法一般通过外界激励系统给物理结构一个外部激励，然后测量某点的响应信号，对激励信号和响应信号在频域上进行处理最后得到传递函数。可以用激振器和力锤两种方法对激励点施加激励。本文在获取频响函数时，使用LMS.test.lab 测试软件Impact Testing模块测试各关键点间X,Y和Z三个方向的传递函数，使用力锤对发动机前后悬置点和排气管前后悬挂点进行敲击测得激励点到参考点，激励点到激励点以及激励点到目标点之间的传递函数。在使用锤击法测量传递函数时，为了减少测量误差，得到更为准确的传递函数，进行多次敲击然后取平均值。图2为部分传递函数测试结果。

2.3.2 关键点响应的获取

在使用传递函数逆矩阵法识别激励点载荷时，不仅需要获取各关键点之间的传递函数，还需获取各关键点位置的响应数据。测试过程中在各个关键点布置三向加速度传感器。响应目标点工况状态下振动加速度,启动发动机，利用LMS.test.lab测试软件中LMS.signature模块测试各关键点振动加速度随转速变化的振动响应信号。对采集的振动信号进行频谱和阶次分析，选取四缸发动机2阶为特征信号进行载荷的识别和传递路径贡献量的分析。

3 激励点载荷识别结果及验证

根据载荷计算公式(9)对4个激励点12条传递路径载荷进行计算，图3为各激励点XYZ三个方向载荷力大小。可以看出，排气管前悬挂Z向振动载荷最大，排气管后悬挂3个方向载荷力较小。

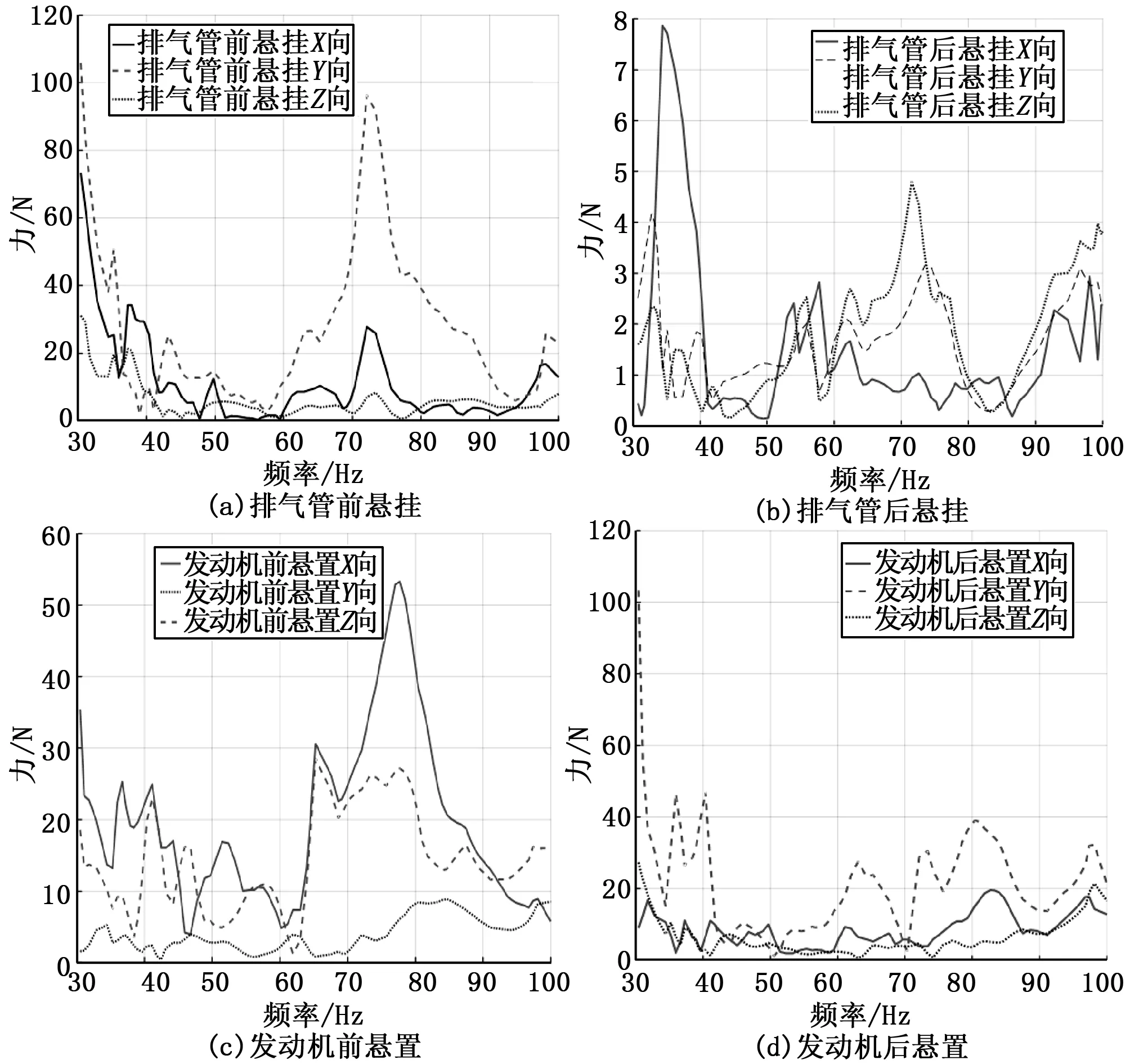
图3 发动机前后悬置XYZ方向载荷

为对逆矩阵法识别的载荷结果进行验证，以座椅导轨和方向盘Z向的振动为例，用识别到的发动机后悬置Z向载荷力结合发动机后悬置Z向到座椅导轨和方向盘Z向的传递函数计算得到座椅导轨和方向盘Z向振动加速度，并于实际测试的结果进行对比，由图4可以看出座椅导轨和方向盘Z向振动计算值与实测值吻合度较高，从而说明利用传递函数逆矩阵法构建的载荷识别模型是可靠的。

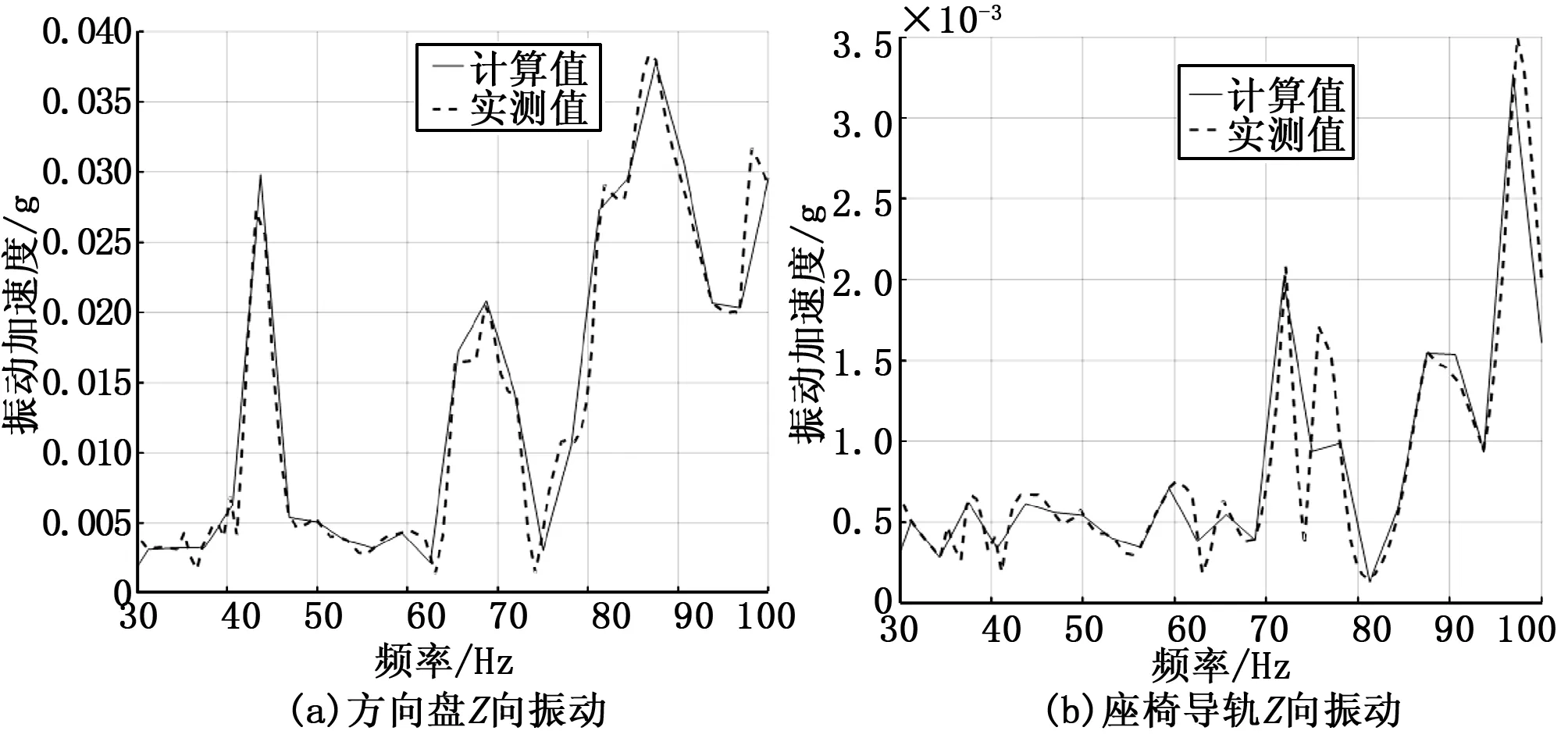
图4方向盘和座椅导轨Z方向振动计算值与实测值的对比

4 振动传递路径贡献量分析

利用识别的激励点的载荷对各传递路径进行贡献量分析，根据公式(9)计算出12条路径对目标点振动的贡献量，图5(a)、(b)分别为各路径对方向盘Z向和座椅导轨Z向贡献量大小的排序，可以看出发动机后悬置点的X向、排气管前悬挂点X向及排气管前悬挂点Y向对方向盘Z向振动贡献量最大，为主要的传递路径；而排气管后悬挂点X向、排气管后悬挂点Y向及排气管后悬挂点Z向的贡献量最小；发动机后悬置点的X向、排气管前悬挂点Y向及发动机后悬置点的Y向对座椅导轨Z向振动贡献量最大，为主要的传递路径，而排气管后悬挂点XY和Z向对座椅导轨Z向振动贡献量最小。

图5 方向盘和座椅导轨Z向各路径贡献量排序

对目标点贡献量分析以后，可以进一步对目标点贡献量较大的关键路径进行传递函数与载荷力的分析，由此可以判断引起目标点的振动是车身结构的传递函数问题还是激励点载荷大小的问题[18]。以方向盘Z向振动为例。

由图6(a)、(b)可以看出在25 Hz和75.5 Hz左右方向

盘有明显的振动峰值，但是激励点到方向盘的传递函数在25 Hz和75.5 Hz左右没有明显峰值，可以得出激励点载荷过大是引起方向盘振动的主要原因。

5 结论

通过构建传递函数逆矩阵对激励点载荷进行识别，并利用识别的载荷计算目标点的振动贡献量，可以得到如下结论：传递函数逆矩阵法识别的载荷计算值与实测值对比结果表明两者的吻合度高，验证了构建的传递函数逆矩阵模型的可靠性；传递路径贡献量分析可以快速准确的诊断汽车关键点振动的原因，并找出影响的目标点振动的关键传递路径；对各路径进行传递函数和载荷力的分析可以诊断出引起目标点振动的原因是的激励点载荷力过大还是所在路径结构传递函数造成的。通过试验测试并基于逆矩阵法的汽车关键点的传递路径分析可以为汽车振动原因的诊断和改进提供理论依据。

[1]Gajdátsy, Péter ákos.Advanced Transfer Path Analysis Methods[D].Katholieke Unversiteit Leuven, 2011.

[2]Vecchio A, Herman VDA, Janssens K, et al. Experimental transfer path analysis of a hybrid bus[J]. SAE Paper, 2005(1):23-35.

[3]Schuhmacher A, Tcherniak D.Engine contribution analysis using a noise and vibration simulator[J]. Sound and Vibration, 2009, 43(1): 16-21.

[4]Tandogan F.O，Gueney A. Vehicle interior noise source contribution and transfer path analysis[J]. International Journal of Vehicle Design, 2010, 52(1-4): 252-267.

[5]Zheng S, Hao P, Lian X, et al.Time-domain transfer path analysis of multiple moving noise sources[J]. Noise Control Engineering Journal, 2011, 59(5): 541-548.

[6]慕 乐,周 鋐.基于传递路径分析的怠速工况下转向盘振动路径识别及改进[J].汽车技术,2011, (4):15-21.

[7]侯锁军,史文库,毛 阳.应用传递路径分析方法对方向盘抖动贡献量的研究[J].西安交通大学学报, 2013, 47(3):132-136.

[8]刘东明,项 党,罗 清，等.传递路径分析技术在车内噪声与振动研究与分析中的应用 [J].噪声与振动控制,2007, 27(4):73-77.

[9]F.X. de Melo, L.P. R. de Oliveira. Development of a test bench for vibro-acoustic studies: TPA study case[A]. International Conference on Noise and Vibration Engineering (ISMA)[C]. Leuven, Belgium, 2012.

[10]Padilha P.E.F，Arruda J.R.D.F.Comparison of Estimation Techniques or Vibro-Acoustic Transfer Path Analysis[J].Shock and Vibration, 2006(13) : 459-467.

[11]Dom S,Geluk T, Janssens K.Transfer Path Analysis: Accurate Load Prediction beyond the Traditional Mount Stiffness and Matrix Inversion Methods. [J] SAE Technical Paper, 2014, 70(2):12-16.

[12]MaartenV，Dennis，Daniel.General framework for transfer path analysis [J].Mechanical Systems and Signal Processing, 2016, 68-69(2):217-244.

[13]宋海生.基于扩展OPAX传递路径方法的轻型客车振动控制研究[D].长春：吉林大学,2012.

[14]龙 岩，史文库，梁天也，等.基于改进传递路径分析法的动力总成悬置系统优化及评价[J].汽车工程, 2009, 31(10):958-962.

[15]Plunt J.Finding and fixing vehicle NVH problems with transfer path analysis[J].Sound and Vibration, 2005, 39(11):12-17.

[16]郭 荣,万 钢,左曙光.燃料电池轿车车内噪声传递路径分析研究[J].汽车工程, 2007, 29(8):635-641.

[17]郭世辉,刘振国,臧秀敏,等.工况载荷下传递路径分析方法[J].噪声与振动控制, 2016, 36(2):105-109.

[18]齐 全，周以齐，崔文玲.传递基于OTPA方法的挖掘机驾驶室结构噪声源识别[J].噪声与振动控制, 2017, 37(2):80-84.