基于面结构光的机械工件三维扫描系统设计

， ，

(华南理工大学 自动化科学与工程学院， 广州 510641)

0 引言

机器人结合机器视觉的技术方案在国内机械制造业中的使用越来越广泛。在机械工件装配过程中，二维机器视觉检测技术存在一定的局限性，使用单一相机只能在平面上获取工件的位置，无法获取深度信息，需人工调整机械工件为固定的位姿，才能实现机器人的抓取操作。而三维机器视觉不仅能够获取到机械工件的平面信息，还能获取到机械工件的深度信息和位姿[1]。

三维扫描技术在国内制造业的模具成型、造型设计方面已经有较广泛的应用，但在国内自动化机械工件拾取和装配属于起步阶段。随着三维扫描技术的应用与发展，其精度、适应性、可靠性等方面已经能够满足自动化机械工件拾取和装配的要求，三维扫描技术在该领域的应用研究也越发热门[2]。

本文设计了基于面结构光的机械工件三维扫描系统。标定策略设计了40%灰度值棋盘格标定板结合100%灰度值棋盘格标定图案技术对工业相机和投影仪进行标定；编码解码策略设计了100%灰度正反格雷码结构光栅结合相移技术对机械工件进行扫描，机械工件调制后的光栅图像由工业相机同步获取，对条纹进行亚像素精度提取；重构策略利用标定的系统内外参数和解码的条纹对应的像素坐标，设计了三角检测算法并结合反复迭代逼近的原则获取机械工件点云，并对背景平面多余点云随机迭代分割，最后在计算机得到机械工件的三维点云模型[3-4]。

1 标定策略

在标定投影仪时，需要投影棋盘格图案到标定板上，同时标定板上也有打印的棋盘格，可能会造成亚像素角点的误检测，导致标定结果和实际值较大的偏差。解决的办法可以采用彩色的棋盘格标定板和投射彩色的棋盘格标定图案，通过研究彩色图案叠加在彩色棋盘格标定板上的颜色特性可以实现两者的部分区分，但是仍然存在角点误检测的状况[5-6]。

本文设计了40%灰度值棋盘格标定板结合100%灰度值棋盘格标定图案的相机-投影仪标定策略。标定策略分为两个部分：相机标定和投影仪标定。其中投影仪的标定需要使用相机标定的结果和参数。以相机模型和张正友标定理论为基础，把棋盘格标定板参考坐标系转换到照片参考坐标系上，通过坐标变换和扭曲形变等计算，得到相机的模型为：

(1)

由于可以把投影仪的模型看作是相机模型的逆变换，因此投影仪的模型表示为：

(2)

设计的标定策略的具体步骤为：调整相机、投影仪、棋盘格标定板之间的位置关系，三者整体呈现一个三角形的方位，使得标定板棋盘格上的角点在相机图像上能够清晰成像，并且投影仪投射在棋盘格标定板上的图案能够完全进入相机的视野内。首先投影仪投射白光，相机拍摄一张棋盘格标定板的图像，需保证棋盘格的角点都在视野范围内；保持棋盘格标定板的位姿不变，投影仪投射棋盘格图案，图案覆盖住标定板上面的棋盘格，此时相机同步拍摄一张叠加有棋盘格图案的棋盘格标定板的图像；改变棋盘格标定板的位姿，重复上面的步骤10次，过程要保持相机和投影仪的相对位置不变，也不能改变相机的焦距。利用拍摄的20张图片通过寻找对应角点的方式标定出相机和投影仪的内外参数。图1所示为相机和投影仪标定图像及检测的投射棋盘格图案。

图1 标定图像及检测的投射棋盘格

系统标定结果如下：

1)相机标定结果：内参:

畸变系数:

kc=[-0.094 0.48 -0.00 080 -0.00 024 -1.49]

2)投影仪标定结果：内参:

畸变系数:

kp=[0.065 -0.20 0.0 012 0.00 043 0.10]

3)投影仪-相机：旋转角度向量:

VR=(-0.023 0.052 -0.0 050)

平移距离向量VT=(-4.607 9.682 24.18)。

标定结果表明采用40%灰度值棋盘格标定板结合100%灰度值棋盘格标定图案的相机-投影仪标定策略能够准确地提取棋盘格的角点，设计合理。

2 解码编码策略

基于比较二进值编码、格雷码编码、相移法等编码解码策略的优点和不足，设计了100%灰度正反格雷码结合相移法的编码解码策略，该策略综合了各编码方案的优点，互相弥补了各编码方案的不足，使得投影图案和拍摄图像像素的误匹配大大降低[7-8]；同时采用亚像素检测算法优化大大提高了像素匹配的准确性[9]。

2.1 100%灰度正反格雷码结合相移法

以5位编码为例，二进制编码是采用5幅投影图案形成25=32个条纹设计的。格雷码由二进制编码改进而来。设有一个二进制编码格式为BnBn-1···B1B0,对应的格雷码编码格式为GnGn-1···G1G0,转换规则为：Gn=Bn且Gi=Bi⊕Bi+1(i≠n)。图2为5位二进制编码和正反格雷码示意图。

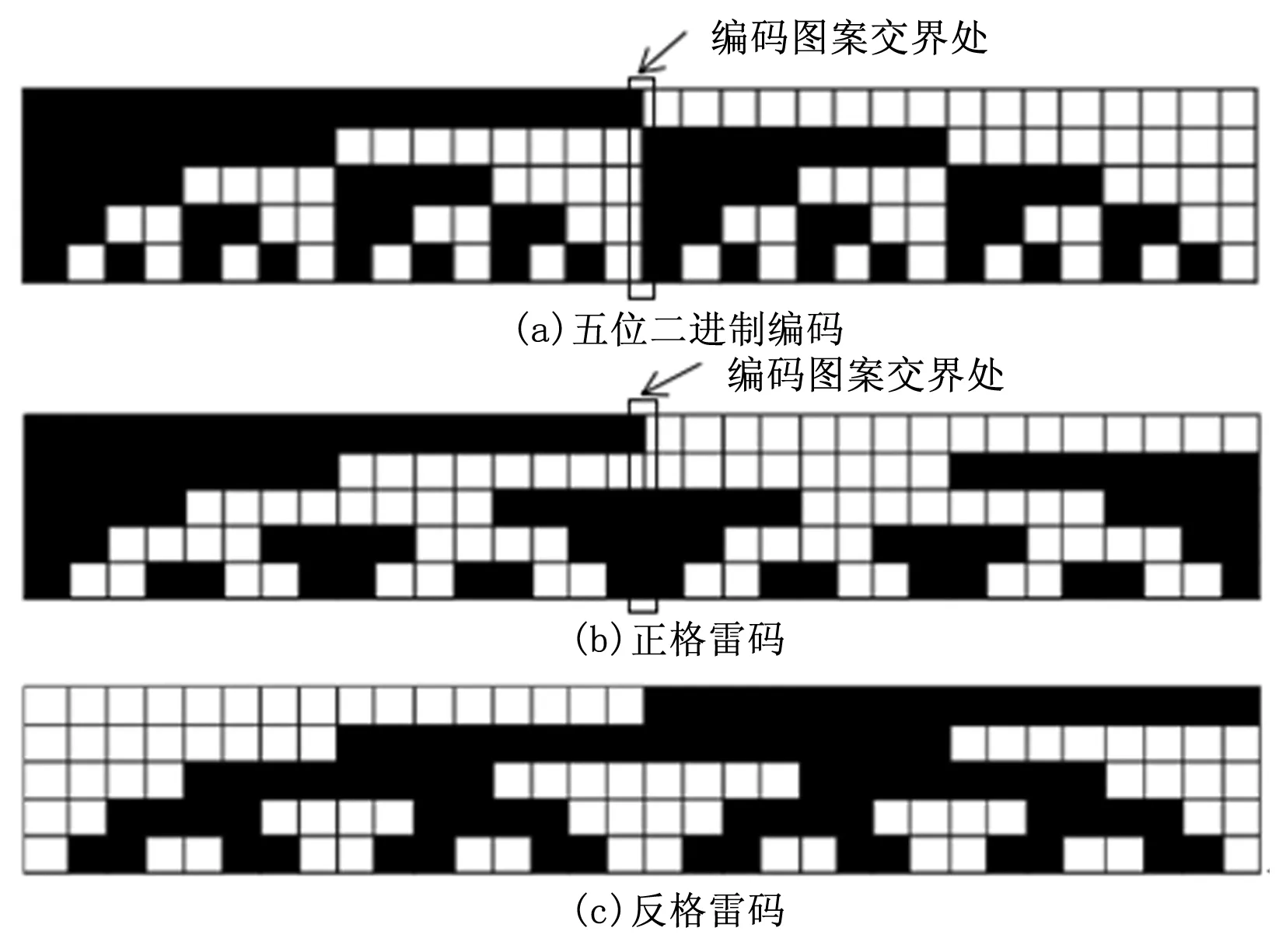
图2 5位二进制编码和正反格雷码示意图

在识别编码图案交界处，二进制编码每一幅都可能造成误识别，而格雷码只有在第1幅可能会造成误识别，后面投射的4幅图案都不会有二义性的问题，因此最大限度地降低了边缘提取和解码的错误率。

理论上格雷码在像素对应条纹的识别上做到了在保持特征区别的基础上把错误率降到了最低，但是在投影仪投射光栅条纹的过程中，格雷码图案会受到扫描系统所处环境和机械工件自身特性的影响，包括系统环境自然光的强弱、光传播的介质、机械工件的反射特性等，导致格雷码的明暗条纹的相互渗透，使得像素的识别结果出现偏差。设计了100%正反灰度格雷码的编码方案，即向机械工件投射n幅100%正向灰度格雷码后，紧接着向该工件投射n幅100%反向灰度格雷码。识别时把对应的100%正反灰度图案作差分运算，能够降低环境因素导致的误识别。

扫描系统同时投射纵向和横向的结构光栅，才能唯一确定二维平面的各个像素点。投影仪分辨率为1 024*960，若仅采用100%正反格雷码的编码方案，横向结构光栅图案个数为log(1 024)=10，纵向结构光栅图案个数为log(960)≈10，理论上能够区分二维平面上每一个像素点。但是条纹宽度只有一个像素对识别算法的实现比较困难，识别结果容易出错。因此最终设计了100%灰度正反格雷码结合相移法的编码解码策略。

相移法是向机械工件表面投射一系列余弦光栅图案，工业相机同步拍摄经过机械工件表面深度调制后的光栅图案，计算出调制后光栅图案中各个像素的相位值，根据该相位值找到投影仪中未调制的余弦光栅图案对应的像素坐标值。调制后的光栅图像灰度值为：

I(x,y)=A(x,y)+B(x,y)cos[φ(x,y)+η]

(3)

其中:I(x,y)为光栅图案像素(x,y)的灰度值，A(x,y)为光栅图案背景灰度值，B(x,y)为光栅图案的调制灰度值，φ(x,y)为调制后的光栅图案像素(x,y)的相位值，η是各幅余弦光栅图案的相位偏移值。

Ii(x,y)=A(x,y)+B(x,y)cos[φ(x,y)+π*i/2]

(i=0,1,2,3)

(4)

解得相位主值为：

(-π≤φ≤π)

(5)

为了区分整个光栅图案的相位值，需要对相位主值展开。本文设计了100%灰度正反格雷码结合相移法的编码解码策略。策略思路就是利用100%正反灰度格雷码光栅对整个投影图案进行粗分，格雷码光栅条纹的个数等于相移法周期的个数，解码时先把格雷码数值转化为二进制数值，该数值为相位主值的周期次数；在每个周期内，像素的相位主值是唯一的，利用相移法对处于同一个周期内的像素进行区分。设计综合了100%灰度正反格雷码编码范围广和相移法编码分辨率高的优点，满足机械工件对三维扫描系统的精度要求。对于整个光栅图案每个像素的绝对相位值表示为：

θ(x,y)=φ(x,y)+2π*k(k为周期次数)

(6)

图3为4位相移法示意图、3位格雷码结合4位相移法示意图。

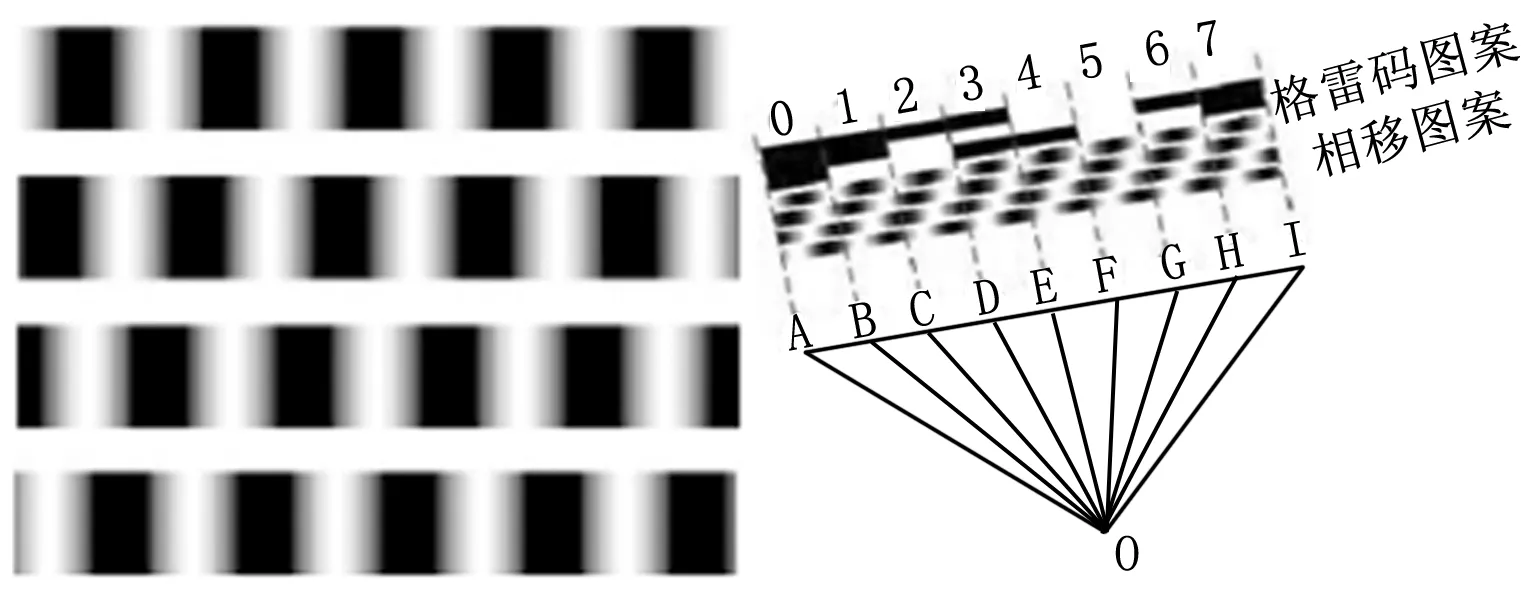
图3 四位相移法(左)和三位格雷码结合四位相移法(右)

图4～6为机械工件扫描实验图。

图4 纵向正反格雷码结构光栅

图5 横向正反格雷码结构光栅

图6 四位相移光栅

2.2 亚像素精度处理

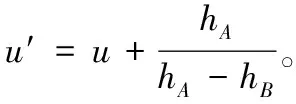
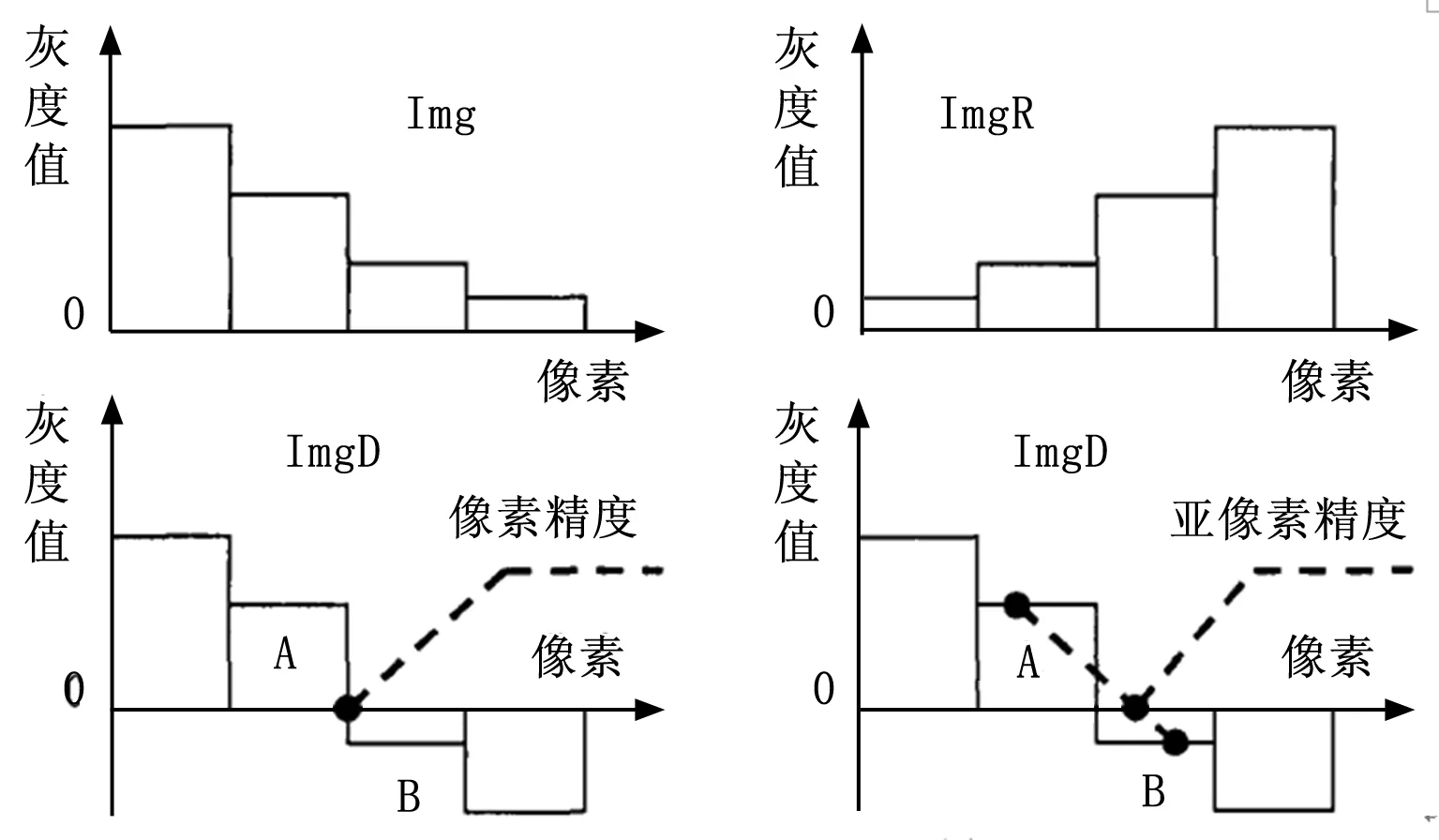
图7 亚像素精度处理

3 重构策略

3.1 三维点云重构

根据相机、投影仪、机械工件在空间中的几何位置关系，设计了基于三角检测算法的点云重构策略[10-11]。以投射纵向的100%灰度正反格雷码结合相移法的结构光栅为例，三维点云重构策略的设计思路如下：获取照片坐标系上被结构光栅覆盖的各点的像素坐标值Ci=(ui,vi)，通过投射的纵向结构光栅可以计算出在投影仪图案参考坐标系中各点对应的像素横坐标值Pui=xi；以及计算得到相机和投影仪的内外部标定参数值。从像素坐标系转化到相机和投影仪成像坐标系时需要进行标准化操作，包括缩放偏移反变换、斜交反变换和畸变反变换。设fc1和fc2分别为相机模型中u轴和v轴方向上的焦距，(u0,v0)为像素坐标系中成像中心的坐标。缩放偏移反变换是把像素单位pixel转化为距离单位mm，同时补偿成像中心的偏移值。缩放偏移反变换后对应点的坐标为：

(7)

斜交反变换是补偿光轴和成像平面斜交导致的坐标偏移，设αc为斜交参数，斜交反变换后对应后点的坐标为：

(8)

畸变反变换是补偿镜头成像时在径向和切向上的坐标偏移，设畸变系数为kc1、kc2、kc3、kc4和kc5，且：

(9)

ki=1+kc1*ri2+kc2*ri4+kc5*ri6

(10)

(11)

畸变反变换后对应点在相机成像坐标系中坐标值为：

(12)

另外对投影仪图案参考坐标系中各点对应的像素横坐标值Pui进行缩放偏移反变换后得到的横坐标值为：

(13)

设相机参考坐标系中坐标Xci到投影仪参考坐标系中坐标Xpi的旋转矩阵和平移矩阵分别为R和T，则：

Xpi=R*Xci+T

(14)

展开得：

(15)

联立上式可得机械工件表面各个点在相机坐标系中的三维坐标为:[uoi*zcivoi*zcizci]T，其中：

(r11*uoi+r12*voi+r13)

(16)

3.2 背景点云去除

重构后的机械工件的点云包括一部分背景平面无关点云[12]，需要去除此部分的点云。根据无关点云位于同一平面内的特点，设计了随机选取点云并反复迭代构造背景平面实现分割的方法。首先从点云集中随机选取部分点计算假定平面的参数，设置一个距离阈值，计算其余点与该平面的距离，大于阈值设为外点，小于阈值设为内点；若内点的个数大于期望的点数，则用内点重新计算平面模型参数作为最终参数，所有的内点即为分割的平面背景；若小于，则与先前最大内点数比较，保留最大内点数对应的平面背景参数。上述步骤反复迭代，直到找到满足条件的平面背景为止。

4 扫描结果与分析

图8是设计的三维扫描系统对3个不同机械工件表面的扫描结果，以棋盘格标定板作为背景。可以看出，扫描出的各机械工件的点云和背景平面点云实现了完全分割，同时能够识别出各工件的表面纹理特征。根据机械工件的实际测量值，本系统重构的点云密度满足精度要求，相邻点云间隔在0.05 mm以内。同时根据点云的三维坐标，可以确定各工件的空间几何信息，包括工件在相机坐标系的位置信息和深度信息。

图8 机械工件点云重构

5 结论

针对制造业中机械工件拾取对三维扫描技术的应用需求，设计了能够重构机械工件表面点云的三维扫描系统。对系统的标定、编码解码、重构过程设计了有效合理的策略，检验了重构的三维点云数据满足精度要求，可以作为机器人运动控制系统的输入信息实现对机械工件的抓取操作。

[1] Liu MY, Tuzel O, A Veeraraghavan. Fast object localization and pose estimation in heavy clutter for robotic bin picking[J]. International Journal of Robotics Research, 2012, 31(8):951-973.

[2] 王厚勇, 张文佳, 辛磊磊.机器人与自动化技术在生产线智能化改造中的应用[J]. 汽车工艺师，2017,3:24-27.

[3] 胡爱玲, 江秀红.基于机械手的结构光视觉测量系统建模[J]. 控制工程，2016,23(3)：449-452.

[4] 胡法荣.基于结构光的三维轮廓测量系统研究[D].杭州：浙江大学,2013.

[5] 申心兰，王 仲，刘常杰，等.一种基于棋盘格的高精度分区域相机标定方法[J].测试科学与仪器，2016,7(4):342-349.

[6] Sun J, Chen X, Gong Z. Accurate camera calibration with distortion models using sphere images[J].Optics & Laser Technology, 2015, 65(65):83-87.

[7] Lilienblum E, Al-Hamadi A. A structured light approach for 3d surface reconstruction with a stereo line-scan system[A].Instrumentation &Measurement Technology Conference[C]. 2015, 64(5):1171-1176.

[8] 赵必玉. 高精度面结构光三维测量方法研究[D].成都：电子科技大学，2015.

[9] 夏阳阳，林 菁.无粗定位亚像素边缘检测算法研究[J].上海师范大学学报，2016,45(4):434-440.

[10] Nagai Y, Ohtake Y, Suzuki H. Tomograghic surface reconstruction from point cloud[J]. Computers & Graphics, 2015, 46:55-63.

[11] Liu C, Yuan D, Zhao H. 3D point cloud denoising and normal estimation for 3D surface reconstruction[A]. IEEE International Conference on Robotics & Biomimetics[C]. 2015:820-825.

[12] Beksi W J, Papannikolopoulos N. 3D point cloud segmentation using topological persistence[A]. IEEE International Conference on Robotics & Automation[C]. 2016:5046-5051.