五轴转向车辆输出反馈鲁棒稳定控制系统设计＊

满绪民 王吉华 李超 梁鹏云 郭栋

（山东理工大学，淄博 255049）

1 前言

随着社会与经济的不断发展，人们对大功率车辆载重能力的要求越来越高，考虑到国家标准对车辆外廓尺寸、质量及轴载的限制，一味地提高每个轴的载重能力，或者降低整车质量已经没有较明显的作用，针对这种情况，增加车轴数量的方法被提出，多轴汽车随之出现[1]。

迄今为止，国内在多轴转向控制策略方面进展较为迅速。王吉华研制了遥控驾驶四轴转向模型车半物理仿真试验系统，建立了车辆模型和控制算法的仿真试验验证平台[2]；庞文杰证明了CMAC-PID控制的多轴转向系统有较高的响应精度和较快的响应速度[3]；叶俊等利用粒子群算法设计了H∞鲁棒控制器[4]；王菁通过仿真试验验证了约束H∞控制方法可以有效提高4WS汽车的操纵稳定性，基于干扰观测器（DOBC）控制的4WS汽车都可以保持汽车的稳定性并降低驾驶员的操纵难度[5]；高峰着重介绍了某五轴双前轴转向重型汽车的建模过程[6]；黄丽杰讨论了不确定模糊时滞系统的鲁棒性能分析和控制器设计问题[7]。这些控制算法也可应用到控制多轴车辆转向[8-9]中去。

本文根据五轴车辆在行驶中受到路面状况、质心高度等参数影响的特点设计了输出反馈鲁棒稳定控制系统。对该系统进行仿真分析表明，五轴转向车辆在行驶过程中可适应参数的变化，从而达到转向稳定。

2 五轴转向汽车二自由度模型

假定在驱动力不大的情况下，不计空气阻力、载荷的变化，忽略地面切向力对轮胎侧偏特性影响效果的前提下，将实际五轴转向汽车简化为单侧的五轮模型。其线性二自由度模型如图1所示，样车部分参数如表1所示。

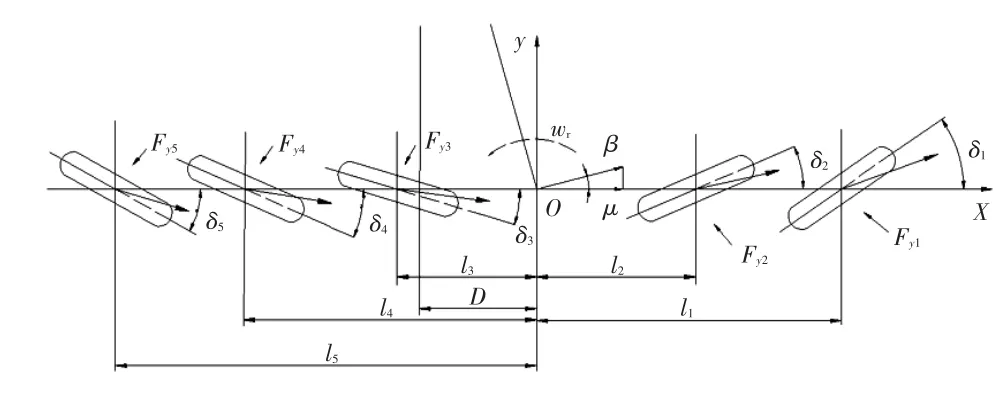
图1 五轴转向汽车二自由度模型

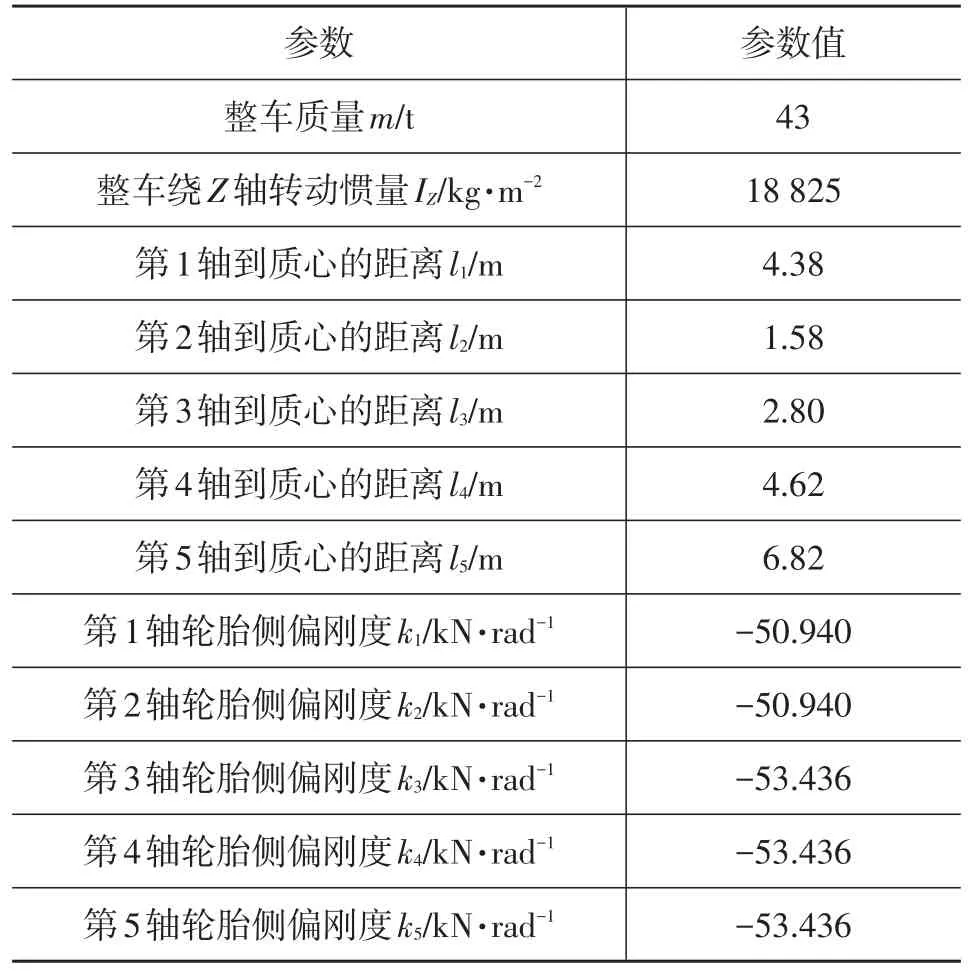
表1 五轴汽车部分参数

根据五轴转向汽车运动参数关系式[10]，推导出二自由度运动微分方程：

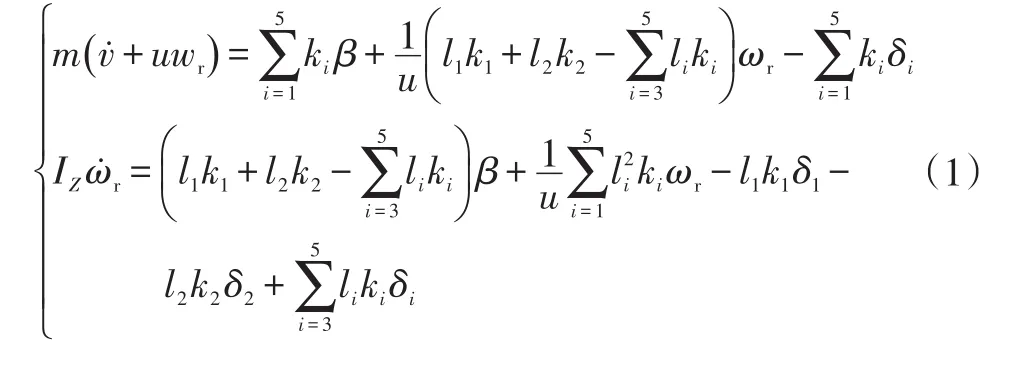
式中，β为质心侧偏角；u为质心前进速度；ωr为横摆角速度；δi为第i轴转向轮转角；v为质心速度。

把多轴车辆动力学模型简化为线性二自由度汽车模型，状态变量x=[βωr]T，输入变量u=[δ1δ2δ3δ4δ5]，输出变量为y，A、B、C为系数矩阵，其状态空间表达式为：

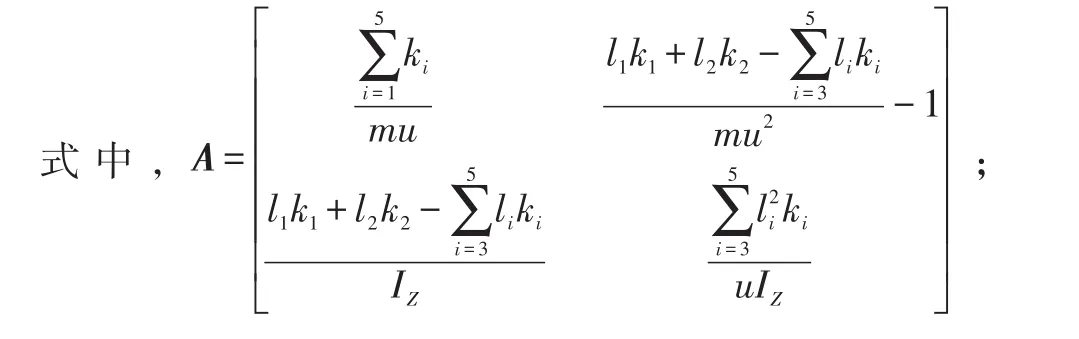
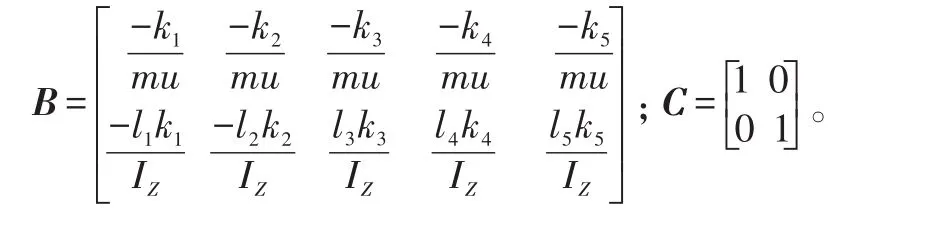
各轴等效转角与前轴转角的比例系数定义为Ki：

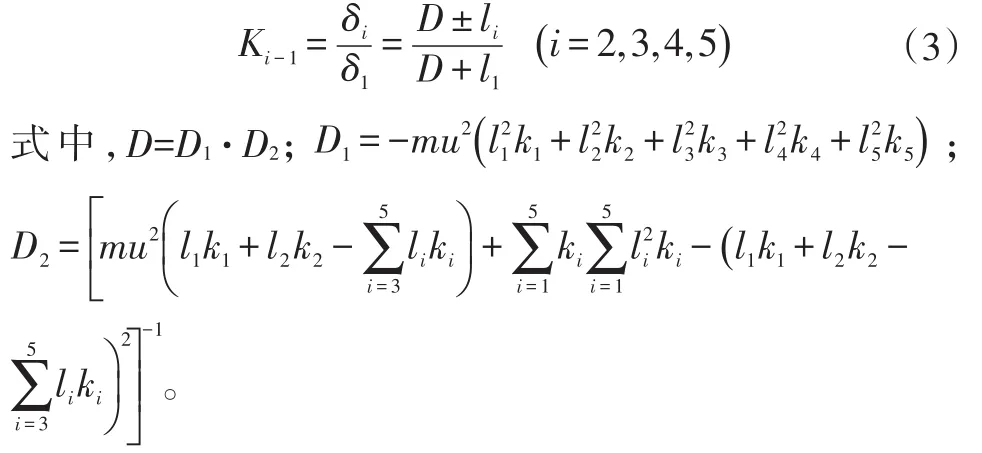
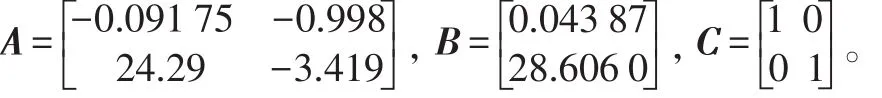
3 具有参数不确定性的鲁棒稳定控制系统设计

3.1 闭环控制系统描述

考虑如下具有参数不确定的多变量系统[11]：

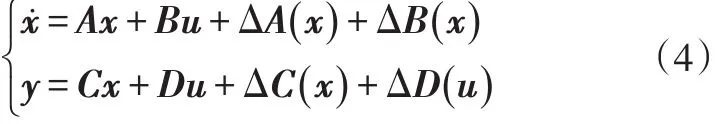
设系统（A、B、C、D）完全可控、可观，且系统的参数不确定为范数有界，记

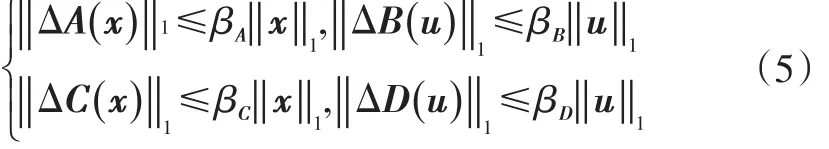
取动态反馈控制器构成如图2所示的闭环系统，动态反馈控制器的方程为：

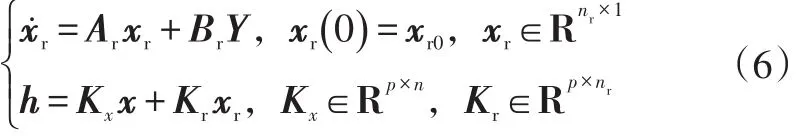
式中，Ar、Br、Kx、Kr为所设计的动态状态反馈控制器的系数矩阵；Y为该控制器的输入变量；xr为该控制器的状态变量；h为该控制器的输出变量。

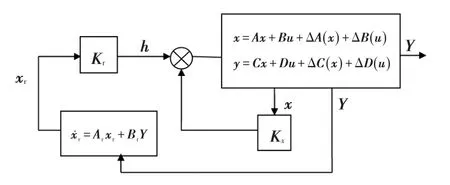
图2 具有参数不确定的闭环系统

设计控制器（Ar、Br、Kx、Kr）的目的是使闭环系统稳定，称此控制器为鲁棒稳定控制器，同时称该系统为鲁棒稳定控制系统[9]。根据图2和式（4）、式（6），可得闭环系统的动态方程，即

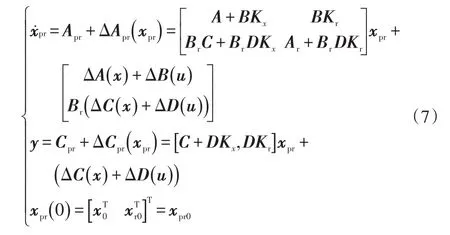
3.2 鲁棒稳定性控制器设计原理

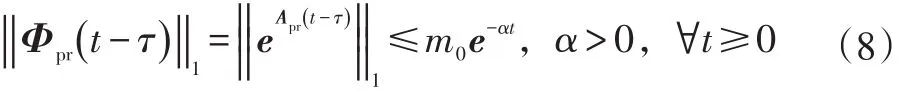
式中，α为区间系统的鲁棒稳定度；m0为可取小于1的常数；为状态空间中的状态转移矩阵，(t-τ)为时间的偏差。

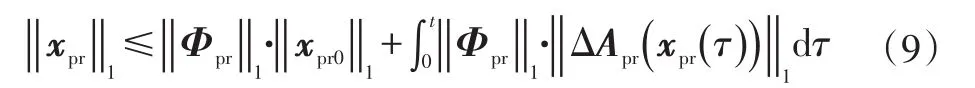
根据式（5）～式（7）可得：

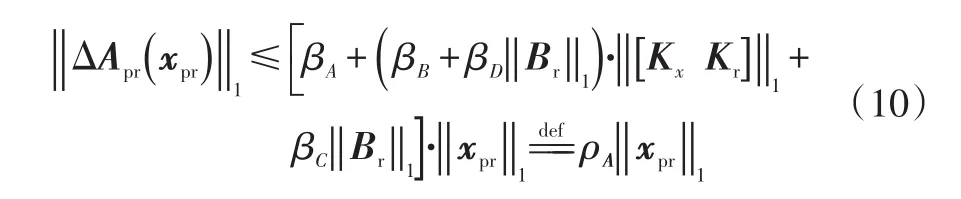
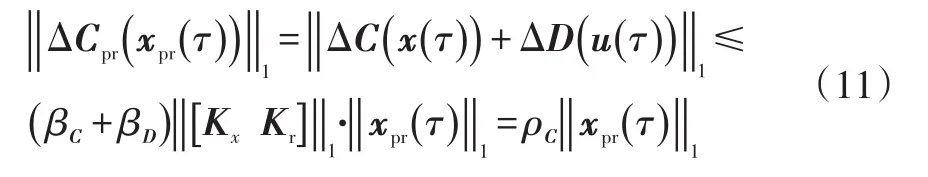
将式（8）和（10）代入式（9），可得：

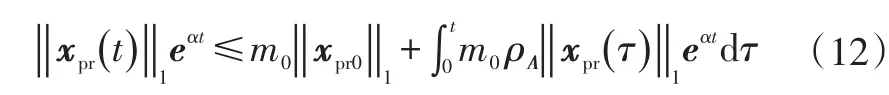
根据Bellman-Gronwall引理将式（12）可整理得：

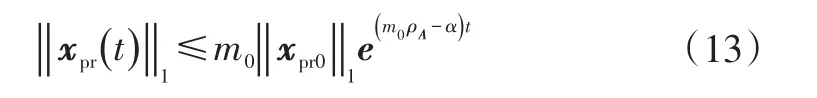
根据式（5）、式（9）、式（11）得：

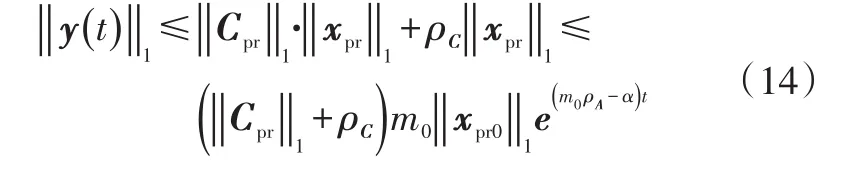
由式（7）和式（14）、式（15）可知，如果闭环系统是鲁棒渐进稳定的，所设计的动态状态反馈控制器（Ar、Br、Kx、Kr）要满足[9]：

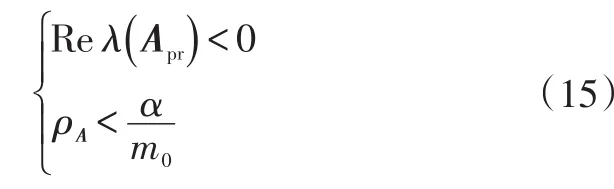
式中，Re表示取复数的实部。

3.3 样车鲁棒控制器设计

针对五轴转向样车，以第1轴转向角度为输入，采用高速（80km/h）工况进行转向稳定性分析，五轴重型样车的部分参数值如表1所示。

按照图2来设计鲁棒控制器，然后根据式（6），针对其不确定性确定控制器参数，通过MATLAB编程计算得到式（7）中矩阵Apr的特征值，如果控制器满足式（15），该条件下的闭环系统一定是鲁棒渐进稳定的。将A、B、C各矩阵代入式（2）得：

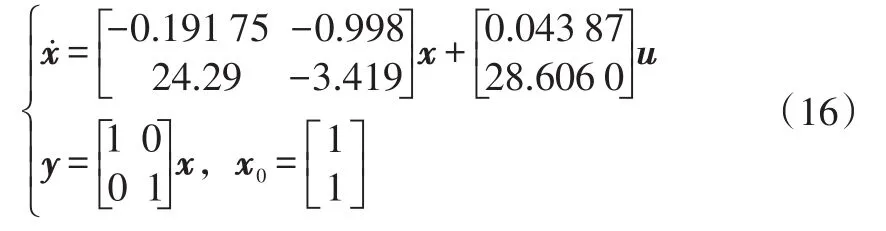
设该线性可变的有界函数为sin(x)，假定该系统经非线性参数摄动后的动态方程为：

按图2设计鲁棒控制器，使摄动系统稳定。根据式（10），有，即βA=1.5，βB=0.2，βC=0，βD=0。下面依次取不确定参数情况1、2、3下的动态控制器，判断所设计的动态状态反馈控制器（Ar、Br、Kx、Kr）是否满足式（15），如满足则可以使控制系统达到较稳定状态。

a. 取不确定参数情况1控制器，令Kx=[-11]，Kr=[10]，可得：

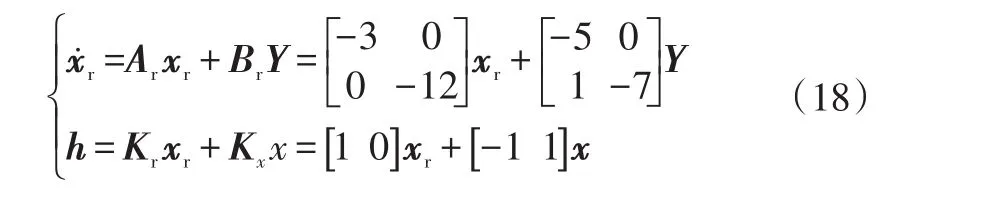
根据式（7）可得闭环系统为：

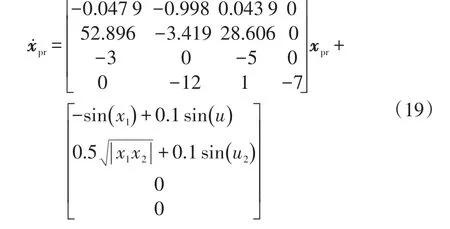
通过MATLAB编程可求得式（19）中矩阵Apr的特征值分别为-7.0000、-2.5469+6.8375i、-2.5469-6.8375i、-3.3730。即得式（8）中的α=2.5469。

b. 取不确定参数情况2控制器，Kx=[1-2]，Kr=[-10]，可得特征值-7.0000、-0.3439+2.8755i、-0.3439-2.8755i、-7.8668。

因ρA=1.9；Reλ(Apr)＜0；α=0.3439，ρA与0.3439/m0的大小不确定，故不确定参数情况2控制器系统稳定性不确定。

c. 取不确定参数情况3控制器，再令Kx=[-22]，Kr=[10]，可得特征值为-3.0000、-2.2673+7.1885i、-2.2673-7.1885i、0.0677。因其中一个特征值的实部大于零，故不确定参数情况3控制器系统不稳定。

4 闭环控制系统仿真

首先，根据能使摄动系统稳定所满足的条件，对该系统进行MATLAB参数计算来设计鲁棒控制器，然后分别建立样车的仿真模型，闭环控制系统的仿真模型和加入前轮转角输入的控制系统的仿真模型，进行Simulink仿真调试，得到并分析各个控制器的输出变量波形，实现了动态控制器对摄动系统的稳定。

4.1 样车开环仿真

据式（19）可建立样车MATLAB/Simulink仿真模型，将第1轴转向轮的转角即前轮转角10°作为输入量，将横摆角速度和质心侧偏角作为输出量，其仿真结果如图3所示。

由图3可知，初始时刻输出变量横摆角速度和质心侧偏角响应值均为0，随着仿真时间的增加，加入前轮转角10°后，两者的阶跃响应值均有明显变化，横摆角速度趋于1.25(°)/s，质心侧偏角趋于1.08°，系统稳定，但操纵稳定性较差。

4.2 不确定参数情况1、2闭环控制系统仿真

将样车模型作为一个子系统，建立闭环控制系统仿真模型，并带入前2组设计的控制器得到不确定参数情况1、2闭环控制系统模型的仿真波形如图4所示。

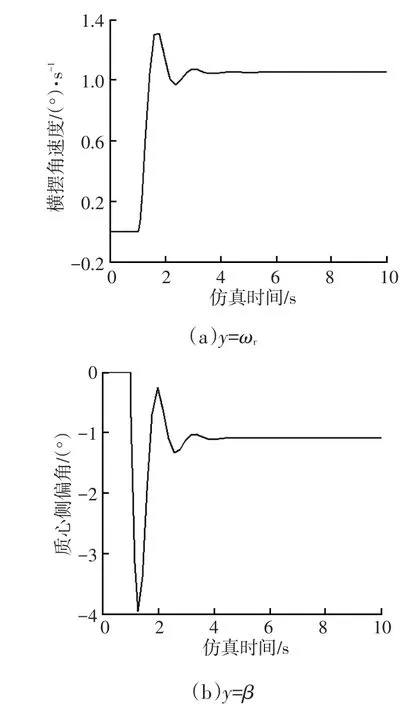
图3 输出变量y=ωr和y=β的波形

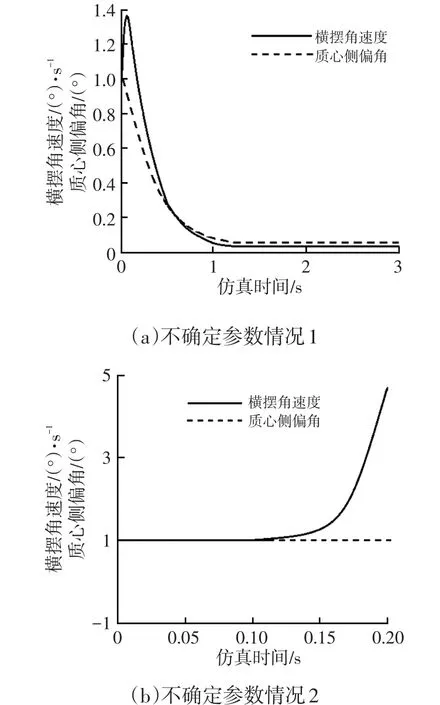
图4 不确定参数情况1、2的仿真波形

由图4可知，在没有控制时，初始时输出变量横摆角速度趋于1.25(°)/s，输出变量质心侧偏角趋于1.08°，随着仿真时间的增加，经过控制后，横摆角速度的响应值趋于0.1(°)/s，质心侧偏角的响应值趋于0.13°，控制系统鲁棒稳定且具有操纵稳定性。在t=0.2s时，不确定参数情况2控制系统输出反馈量极为不稳定，因此，不确定参数情况1控制器最优化。

4.3 加入前轮转角输入的不确定参数情况1控制系统的仿真

为了进一步验证本文的控制算法，样车在不确定参数情况1下，对于图4a中的样车闭环控制响应1s时，在前轮已偏转10°的基础上继续偏转7°，进行闭环控制系统仿真，其仿真结果波形如图5所示。

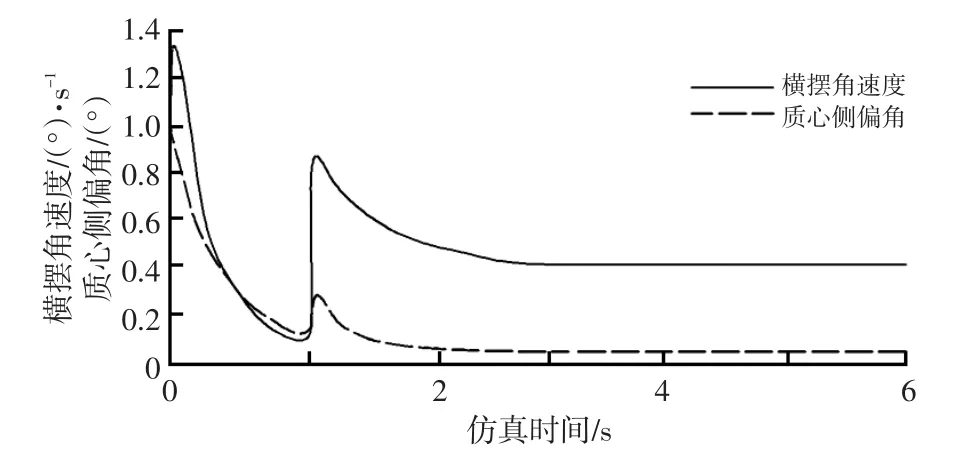
图5 6秒过程的输出波形

由图5可知，初始时输出变量横摆角速度和质心侧偏角初始值分别在1(°)/s和1°附近，在t=1s时，加入前轮转角输入时，横摆角速度和质心侧偏角波形瞬间均发生跳动，随后两者响应波形均逐渐趋于稳定。在t=3s时，横摆角速度的响应值趋于0.4(°)/s，质心侧偏角的响应值趋于0.06°，经仿真验证了不确定参数情况1闭环控制系统的控制器设计可行，系统在3秒时得到了稳定控制而且具有较好的操纵稳定性。

5 结束语

本文首先建立了五轴转向二自由度汽车模型，将汽车模型的微分方程转化为状态空间进行描述，由输入和输出建立出具有参数不确定性的鲁棒稳定闭环控制系统，并对该系统进行MATLAB/Simulink仿真分析，设计的控制系统在五轴转向过程中，鲁棒适应参数的变化，达到转向稳定。

[1]张小江，高秀华，赵建国，等.多轴转向车辆零质心侧偏角控制策略研究[J].农业装备与车辆工程，2008（6）：13-15.

[2]王吉华.多轴转向车辆状态估计与控制研究[D].南京：南京航空航天大学，2013.

[3]庞文杰，王云超，叶存达，等.多轴车辆转向系统神经网络控制算法研究[J].计算机仿真，2015（6）：172-176.

[4]叶俊，黄勇，闫杰.基于粒子群算法的H∞鲁棒控制器设计研究[J].科学技术与工程，2012，12（14）：3411-3414.

[5]王菁.线控四轮转向汽车的鲁棒控制研究[D].长春：吉林大学，2016.

[6]高峰.多轴汽车的操纵稳定性研究及转向机构优化[D].锦州：辽宁工业大学，2015.

[7]黄丽杰.基于T-S模糊模型的时变时滞系统的鲁棒控制研究[D].大庆：东北石油大学，2015.

[8] Watanabe K， Yama kawa J， Tanaka M， et al. Turningcharacteristics of Multi- axle vehicles[J]. Journal of TerraMechanics，2007，44（1）：81-87.

[9] Huh K， Kim J， Hong J. Handling and driving characteristicsfor six wheel vehicles[J]. Journal of Automobile Engineering，2000，214（2）：159-170.

[10]王吉华，魏民祥，杜言利，等.基于T-S模糊模型的多轴转向车辆H∞鲁棒控制[J].交通运输工程学报，2012，12（4）：42-49.

[11]姜长生，吴庆宪，陈文华，等.现代鲁棒控制基础[M].哈尔滨：哈尔滨工业大学出版社，2005.