正碰中假人小腿y向弯矩与x向剪切力间的关联性研究

商恩义 韩刚 柳惠君 张毅

（浙江吉利汽车研究院有限公司，浙江省汽车安全技术研究重点实验室，杭州 311228）

1 前言

中国新车评价规程（C-NCAP）中规定有正面全宽碰撞试验。试验中，试验车上安放假人，该假人小腿上端和下端分别装有传感器。对于碰撞过程中传感器采集到的数据，由于假人脚下运动复杂，小腿与仪表板接触方式千变万化，加上可能发生的仪表板变形、防火墙侵入等影响，各数据的变化规律性差，如果分别独立分析，对小腿伤害过程及造成伤害的原因很难作出明确判断。

另外，C-NCAP中，对假人小腿伤害的评价通过小腿轴向力Fz和小腿胫骨性能指标TI确定，其中，TI通过小腿的x向和y向弯矩计算得到[1]。评价过程中，在小腿上、下2个传感器位置分别评分，选取得分最低者作为最终结果。相关研究表明，正面碰撞试验中，在脚掌未发生背屈崴脚的情况下，假人小腿上端TI大于小腿下端TI，造成小腿上端TI偏大的主要原因是上端y向弯矩偏大[2]。在脚掌发生背屈崴脚的情况下，假人小腿下端TI偏大，原因是下端y向弯矩偏大[3]。

基于此，本文针对脚下结构无明显变形、脚掌未发生背屈和脚下结构发生向后侵入变形、脚掌发生背屈两种工况，分别研究了小腿上端y向弯矩和下端x向剪切力、下端y向弯矩和上端x向剪切力之间的关联性，以此降低假人小腿试验数据的复杂性，提升小腿伤害原因分析的准确性，为仿真分析明确优化方向。

2 假人小腿数据间关系式

假人小腿结构如图1所示，为钢结构，踝关节为球节。在假人小腿上端和下端分别嵌有载荷传感器，传感器之间的距离约为0.24m[4]。试验中，通常测量x向剪切力（上端剪切力为Fxv，下端剪切力为Fxl，脚踝向前、膝盖向后为正）、z向力（轴向力，向下为正）及x向弯矩（上端弯矩为Mxv，下端弯矩为Mxl，膝盖不动、脚踝向左为正）和y向弯矩（上端弯矩为Myv，下端弯矩为Myl，膝盖向后、脚踝向前为正）[5]。

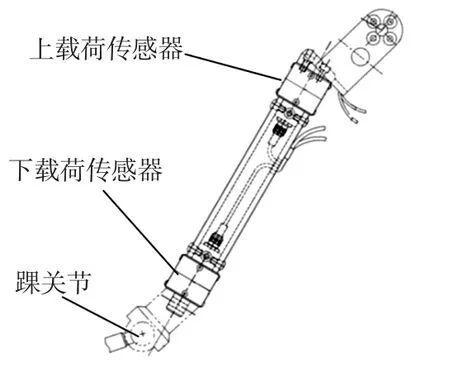
图1 假人小腿内部结构及传感器布置

碰撞过程中，当将上端传感器所采集载荷Myv作为输入时，对应下端传感器位置除产生y向弯矩外，x向也应产生一定剪切力与之平衡。同理，当将下端传感器所采集载荷Myl作为输入时，对应上端，x向也应产生与之平衡的剪切力。换言之，Myv与Fxl、Myl与Fxv之间应存在一定联系[6-7]，建立关系式：

式中，dl和dv为力臂。

接下来，研究式（1）和式（2）成立的可能性及条件。

3 脚掌无背屈条件下Myv与Fxl的关联性

在脚下结构无变形侵入、脚掌无背屈的情况下，可视大腿为力的输入端，脚掌仅受阻止约束，因此，可将歇脚板固定，大腿作为力的输入端进行静压试验、线性冲击试验。鉴于台车试验车身前端不变形，也可通过台车试验进行脚掌无背屈情况下的Myv与Fxl关联性研究。

统计分析了14款车驾驶员假人左小腿的摆放角度，其中，最小角度为34°，最大角度为58°，平均角度为49.4°。前排乘员在乘车过程中，大腿与地板近似平行，因此，当小腿与地板成49.4°时，大腿与小腿之间的夹角近似为130.6°。依据此分析结果，后续研究中主要分析大腿与小腿之间的夹角在120°～150°，即小腿的摆放角度在30°～60°之间的情况。

3.1 静压试验

在万能材料试验机上，对假人小腿进行了2次静压试验。试验中，假人小腿的安装方式如图2所示，为便于固定，在大腿与小腿连接过程中将大腿旋转了180°。

图2 静压试验中假人小腿摆放姿态

3.1.1 第1次静压试验

将小腿与大腿之间夹角调整至120°，即小腿与水平面成30°，进行第1次试验。试验后，根据式（1）试取dl建立Myv与Fxl之间的关系，当取dl=0.21m，接近小腿上、下传感器间的距离0.24m时，Myv与dlFxl曲线基本重合，如图3所示。

图3 静压试验中dl=0.21m时小腿Myv与dlFxl的关系

3.1.2 第2次静压试验

将小腿与大腿间夹角调整至135°，即小腿与水平面成45°，设置压头的下压速度和最大压力与第1次试验相同。第2次试验后，根据式（1），试取dl建立Myv与Fxl之间的关系。最终，dl取值近似为0.15m，接近小腿上、下传感器间距离的一半时，曲线近似重合。

3.1.3 小结

静压试验结果表明，在静压下，上端输入的弯矩几乎完全由下端产生的剪切力平衡，剪切力力臂长度与假人小腿和大腿之间的夹角有关，夹角越大力臂越小：当夹角处于135°（小腿与地面成45°）时，力臂的长度接近上、下传感器间距离的一半，小腿产生对折的趋势明显；当夹角处于120°（小腿与地面成30°）时，力臂增大，更接近上、下传感器之间的距离。

3.2 动态冲击试验

利用线性冲击试验设备对假人小腿进行动态冲击试验研究。假人小腿摆放如图4a所示，小腿与地面成60°。实际碰撞试验中，大腿由于惯性前冲，可以绕臀部关节转动，因此，为了尽可能地模拟实际碰撞中大腿的运动姿态，将推动装置与大腿连接处采用近似球节（在空间上有约20°的自由活动角度）的连结方式。试验时，将推杆推出的最高速度设定为1.5m/s，设定冲击推杆的推动行程为200mm。

试验后，假人小腿姿态如图4b所示，假人脚部未发生任何移动。实车碰撞中，假人脚部将随着小腿向前窜动，动态冲击试验结果表明，该试验未能完全真实地反映整个碰撞过程中假人小腿的运动及受到的伤害，但反映了脚掌被约束后的试验过程，试验结果能够用来进行小腿伤害研究。另外，动态试验与实车碰撞试验之间的差异也反映了实车碰撞中假人小腿及脚部向前运动是由于其自身的惯性，而非大腿对其向前推动的结果。

图4 动态冲击试验前、后假人小腿姿态

根据式（1）试取dl建立Myv与Fxl之间的关系，当取dl=4.3m时，整个过程中曲线近似重合，如图5所示。该结果表明，虽然dl的取值不小于0.24m，与静压试验表现不同，但式（1）适用，对于dl偏大，应和推杆与大腿连接方式与实际不符和推杆角度不可调有关。

图5 动态试验中dl=4.3m时小腿Myv与dlFxl的关系

3.3 台车试验

借助台车试验对假人小腿Myv与Fxl间的关联性做进一步研究。为了降低小腿在运动过程中的复杂性，选取一款SUV的台车开展研究。试验中，驾驶员假人左小腿的摆放角度为58°，碰撞过程不同时刻状态如图6所示。

图6a中，碰撞后前14ms，大腿与小腿保持相对静止状态。比较图6a与图6b，约第14ms后，大腿和小腿整体向前平动。比较图6d与图6c中假人小腿和大腿角度，约第34ms时，脚掌不再向前窜动，随后，膝部开始产生弯曲，大腿绕小腿向上转动，约第40ms时，膝部接触仪表板。与图6c相比，图6d中假人小腿角度略大，表明第40～45ms期间，膝部撞击仪表板后仪表板发生快速变形。第45ms后，小腿受仪表板约束中止向前运动。

根据式（1），取dl=0.12m，建立驾驶员假人小腿Myv和Fxl间对比关系如图7所示。

图6 碰撞过程驾驶员侧假人不同时刻状态

图7 dl=0.12m时假人小腿Myv与dlFxl的关系

图7中，约第45ms之前，Myv与dlFxl曲线重合较好；其后，两曲线重合性较差，但形状相似，表明取dl=0.12m对后续阶段不适合。考虑到第45ms之后膝部与仪表板发生挤压后相对静止，另外，两次静压试验中，随着大腿和小腿间夹角减小，即小腿角度增大，dl取值应越大，以及随着膝部与仪表板的挤压僵持，小腿角度已经很大，故取dl=0.15m，再次建立小腿Myv和Fxl间关系如图8所示。图8中，约50～70ms区间重合较好。

图8 dl=0.15m时假人小腿Myv与dlFxl的关系

图7和图8中，dl分别取0.12m和0.15m，使式（1）分阶段成立，很好地反映了动态冲击中系数关系存在，以及静压试验中当小腿和大腿之间的夹角小于135°时对折点上移的特性。

台车试验结果表明：碰撞过程中式（1）分阶段成立。

3.4 实车试验符合性检验

随机检验了11次实车正面全宽碰撞试验结果，经三坐标测量数据分析、试验前、后假人脚下位置照片对比分析，确认10次碰撞试验中驾驶员假人脚下结构无后侵变形，其中，包括1次56km/h正面全宽碰撞、1次64km/h正面全宽碰撞和1次带膝部气囊的50km/h正面全宽碰撞试验的试验数据。以某车56km/h正面碰撞试验结果为例，检验驾驶员侧假人左小腿数据对式（1）的符合性。

根据式（1），分别取dl=0.12m和dl=0.15m，建立假人左小腿Myv和Fxl间对比关系如图9所示。

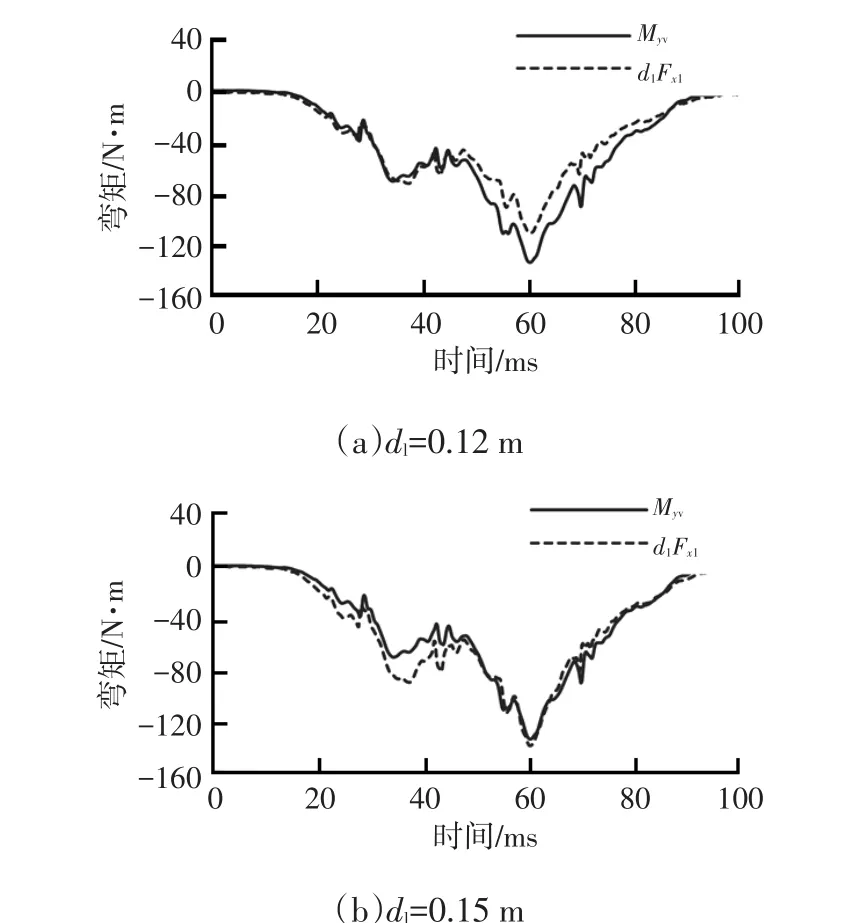
图9 dl不同取值条件下假人小腿Myv与dlFxl的关系

图9a中，约第45ms之前，Myv与dlFxl曲线重合较好。图9b中，约第45ms之后，Myv与dlFxl重合较好。该结果表明式（1）分阶段成立。整个碰撞过程中，驾驶员假人左小腿表现为对折趋势明显，碰撞后期Myv值较大，为失分点。Myv值后期较大的主要原因非力臂突然上升所致，而是Fxl迅速增强造成，因此，后续优化过程应从降低小腿Fxl入手，如调整歇脚板的角度、基础刚度来减弱脚掌的受阻止强度，增强安全带腰带的约束作用来缓解臀部的前冲程度进而缓解小腿的前挤强度等。式（1）在此试验结果中的运用使造成小腿Myv偏大的原因分析一目了然，使后期优化点的确定更加集中。

分析式（1）成立的普遍性。针对假人脚下无后侵变形的其它9次试验，依次试取dl，分析结果是各试验中式（1）均成立，但个别试验中dl的取值并不稳定，如起步阶段和与仪表板碰撞过程中均取dl=0.15m，而两个阶段之间却出现取dl=0.12m的情况；起步阶段取dl=0.12m，与仪表板碰撞过程中取dl=0.16m，而后再次出现取dl=0.14m的情况。造成dl取值发生前述变化的原因，通常为小腿起步阶段运动速度的差异、大腿与小腿之间角度的差异，碰撞过程中仪表板刚度的大小差异、小腿与仪表板接触时角度不同的影响等等。因此，利用式（1）进行约束系统优化时，确认dl取值变化的影响因素，恰好是分析的目的所在，可以为后续CAE工作明确方向。

4 脚掌背屈条件下小腿Myl与Fxv的关联性

脚掌在发生背屈时可视为力的输入端，因此，利用假人足部标定装置固定大腿，用推力计推前脚掌中心，模拟歇脚板或脚踏板后侵情况下小腿Myl与Fxv的关系。

4.1 脚掌摆正静推试验

如图10所示，将大腿前端固定，摆正脚掌，使大腿轴线、小腿轴线与脚掌中截面处于同一平面内，并将脚掌推向小腿消除自由转动角度，而后，用40N左右的推力向斜向下方推前脚掌中心位置。试验后，依据式（2），试取dv建立Myl与Fxv之间的关系如图11所示。图11中，当取dv=0.23m时，两曲线吻合较好。

图10 脚掌摆正静推试验

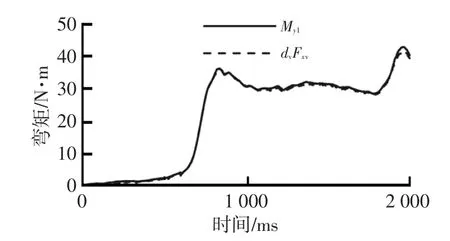
图11 dv=0.23m时假人小腿Myl与dvFxv的关系

4.2 脚掌侧扭静推试验

如图12所示，将大腿前端固定，摆正大腿和小腿，并侧扭脚掌，使脚掌的中截面与大腿和小腿轴线所处的平面成30°，同时，将脚掌推向小腿消除自由转动角度，而后，用40N左右的推力向斜向（如图12所示）推前脚掌中心位置。试验后，试取dv建立Myl与Fxv之间的关系，当取dv=0.2m时，两曲线吻合较好，如图13所示。

图12 脚掌侧扭静推试验

脚掌静推试验表明，当歇脚板或脚踏板后侵导致脚掌发生背屈时，小腿Myl与Fxv间存在稳定的关系，式（2）成立，式中，dv取值接近上、下传感器之间的距离0.24m。

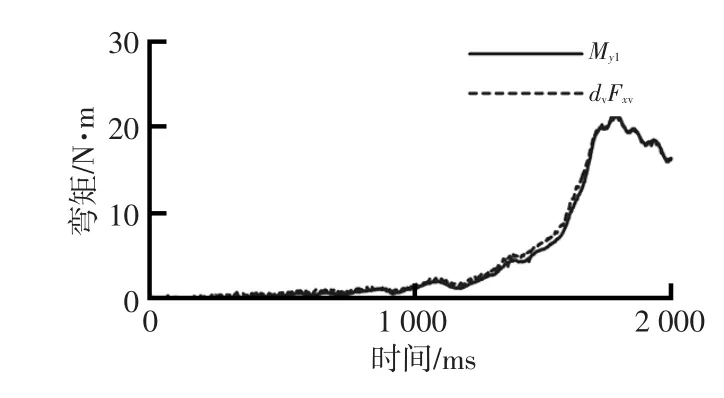
图13 dv=0.2m时假人小腿Myl与dvFxv的关系

4.3 实车试验符合性检验

某款车50km/h正面碰撞试验三坐标测量结果为脚掌位置侵入15mm，脚后跟位置侵入5mm，歇脚板发生内翻式侵入，试验后歇脚板位置如图14所示，歇脚板向后侵入明显，也反映试验中前脚掌发生了背屈。

图14 试验后驾驶员假人左脚位置

检验式（1）的符合性。取dl=0.12m时，驾驶员假人小腿Myv和dlFxl的关系如图15所示，在第53ms后，曲线不再重合，且其趋势完全不同，不存在简单的dl值能使其重合的可能性。另外，第53ms后若要取dl值，与通常式（1）中dl后期取值应增大的趋势将完全相反，dl的取值将减小。因此，此试验中式（1）不成立。

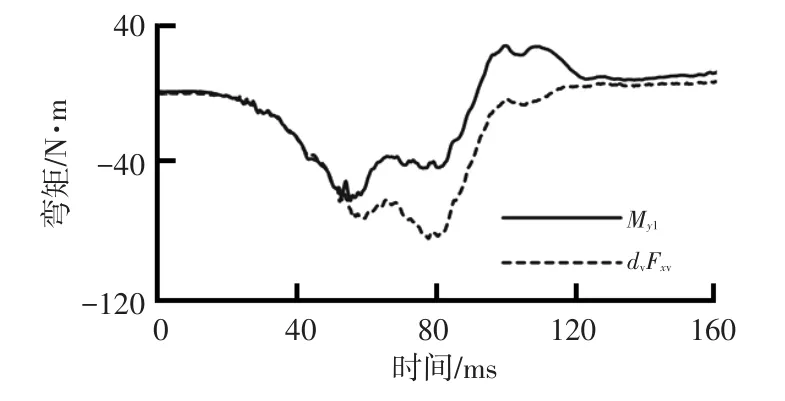
图15 dl=0.12m时假人小腿Myv与dlFxl的关系

依据式（2）建立小腿Myl和Fxv间的比较关系，取dv=0.24m时曲线全程接近吻合，如图16所示。该结果表明，碰撞试验中，当防火墙、歇脚板向后侵入时，假人脚部将成为力和力矩的输入端，此种情况下Myv和Fxl间的关联关系不完全成立，而Myl和Fxv间的关联关系成立。再次分析图16，第53ms之后，小腿下端y向弯矩由负转向正向，且最大值达到91N·m，该值直接导致左下TI达到0.47，超标失分（TI=0.4为满分点，TI=1.3为零分点）。小腿下端Myl正向表明脚掌受力，正向值导致失分则表明歇脚板上端内侵较大，假人脚掌背屈严重[8-9]。

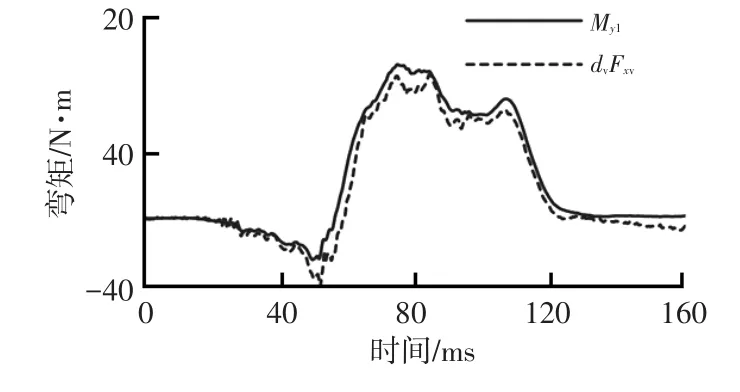
图16 dv=0.24m时假人小腿Myl与dvFxv的关系

5 结束语

研究表明，在正面全宽碰撞试验中，有以下结论：

a.脚下结构无侵入时，假人小腿上端y向弯矩几乎完全由下端x向剪切力平衡。小腿运动时，剪切力力臂约为上、下载荷传感器距离的一半，即0.12m，小腿对折趋势明显；小腿与仪表板挤压相对静止时，对折点上移，力臂增大，通常为0.15m；

b.脚下结构后侵导致脚掌发生背屈时，假人小腿下端y向弯矩几乎完全由上端x向剪切力平衡，剪切力力臂约为上、下载荷传感器距离0.24m。

[1]中国汽车技术研究中心.中国新车评价规程（C-NCAP）[S/OL].[2018-02-08].http://www.c-ncap.org/upload/201707/03181009g2ci.pdf.

[2]孙振东，朱海涛，刘玉光.正面碰撞试验中乘员小腿伤害特性研究[C]//中国汽车工程学会.第五届国际汽车交通安全学术会议论文集，2007.

[3]商恩义，岳国辉，刘珍海，等.偏置碰撞中驾驶员假人脚掌翻转对小腿伤害的影响[J].汽车技术，2016（1）：47-51.

[4] USA Society of Automotive Engineers. User's Manual for the50thPercentile Male Hybrid Ⅲ Test Dummy[S]，1998.

[[5] USA Society of Automotive Engineers. Instrumentation forImpact Test – Part1 – Electronic Instrumentation， REV.MAR95: SAE J211-1[S]，2003.

[6]商恩义，高劲松.A级车正面全宽碰撞试验中假人小腿伤害研究[J].汽车技术，2012（7）：5-9.

[7]张春林，崔来友，谈诚，等.人体足底受力测试及其分析[J].北京理工大学学报，2004（7）：567-570.

[8]商恩义.正面偏置碰撞中座椅刚度低对假人小腿伤害的影响[J].汽车技术，2016（10）：28-32.

[9]商恩义，刘卫国，周大永，等.正面碰撞试验中坐垫刚度无效性对乘员伤害影响研究[J].汽车技术，2017（7）：19-23.