机载光电转塔系统轴系误差数值分析

余 驰

(庆安集团有限公司航空设备研究所,西安 710077)

0 引言

机载光电转塔系统是一种广泛应用于无人机、固定翼飞机和旋翼机等载机平台的高精度光电探测设备[1],它随着精密传动技术、随动控制技术、光学技术、传感器技术和图像处理技术的发展和应用，朝着高精度和高分辨率的方向发展[2-3]。机载光电转塔系统一般通过多轴运动合成实现对一定空域目标和区域的探测和监控，轴线的指向精度是实现高精度探测、态势感知和环境监控的基础。在高精度的机载光电转塔系统中，加工误差、结构变形误差、配合与安装误差、成件精度等均会通过几何关系耦合到方位轴和俯仰轴，最终表现为产生相应的合成轴系误差。因此在不同的应用领域对轴系误差的控制研究备受关注[4-11]，也是决定随动跟踪精度的重要因素之一。

这些误差可以通过系统设计控制和降低，但却是不可避免的存在。为了消除误差、提高精度，本文建立了机载光电转塔系统轴系误差的数学模型，推导出了因轴系误差在方位和俯仰方向产生随动跟踪误差的影响关系，并进行了仿真与分析，提出了将误差角度作为位置环的补偿引入到随动控制中，消除误差，提高随动精度的解决方法。

1 轴系误差数学模型建立与分析

机载光电转塔系统轴系关系见图1，Y框为方位框，P框为俯仰框，以实现在方位和俯仰两个自由度的随动。建立载体坐标系OXaYaZa、机载光电转塔系统方位框坐标系OXyYyZy和俯仰框坐标系OXpYpZp。α，β分别为方位框坐标系OXyYyZy和俯仰框坐标系OXpYpZp绕OZa和OXy旋转的方位角和俯仰角。

图1 机载光电转塔系统轴系关系图Fig.1 Shafting relationship of airborne optical-electronic turret system

OXaYaZa坐标系中向量R，分解到OXaYaZa坐标系中3个轴的分量分别为Rax,Ray,Raz。在不考虑轴系误差时，Rax,Ray,Raz通过OZa轴的摩擦和几何约束耦合到方位框中，可以得到Rax,Ray,Raz分解到方位框坐标系3个轴的分量分别为Ryx,Ryy,Ryz，如图2、图3所示,其算式见式(1)。

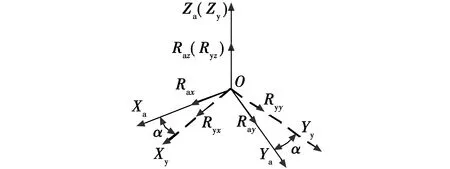
图2 方位与载体坐标系的关系图Fig.2 Relationship between yawing and aircraft coordinate system

(1)

式中：

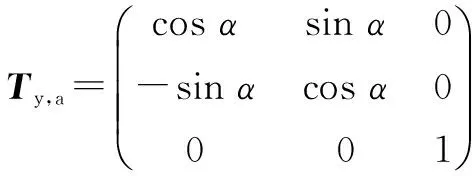
(2)

图3 俯仰与方位坐标系的关系图Fig.3 Relationship between pitching and yawing coordinate system

Ryx，Ryy，Ryz通过OXp轴的摩擦和几何约束耦合到俯仰框中，可以得到Ryx,Ryy,Ryz分解到俯仰框坐标系3个轴的分量分别为Rpx,Rpy,Rpz。即

(3)

式中：

(4)

Tp,a=Tp,yTy,a

(5)

(6)

在考虑轴系误差时，设θ为方位轴误差角度，γ为俯仰轴误差角度，如图4所示。

图4 机载光电转塔系统轴系误差关系图Fig.4 Relationship of axial system error of airborne optical-electronic turret system

因为轴系误差的存在等效于OXaYaZa坐标系绕OZa和OXa1旋转了一个θ和γ的旋转角，OXaYaZa坐标系绕OZa旋转θ角形成了OXa1Ya1Za1坐标系，OXa1Ya1Za1坐标系绕OXa1旋转γ角形成了OXa2Ya2Za2坐标系。则OXaYaZa坐标系中的向量R，3个轴的分量为Rax，Ray，Raz在OXa1Ya1Za1坐标系和OXa2Ya2Za2新坐标系的分量分别为Rax1，Ray1，Raz1和Rax2，Ray2，Raz2。

(7)

式中：

(8)

Rax1，Ray1，Raz1通过OXa1轴旋转γ角，可以得到Rax1，Ray1，Raz1在OXa2Ya2Za2坐标系3个轴的分量分别为Rpx2，Rpy2，Rpz2，即

(9)

式中:

(10)

(11)

(12)

因为轴系误差θ和γ的存在，在OXaYaZa坐标系中的向量R，分解到OXa2Ya2Za2坐标系中3个轴的分量分别为Rax2，Ray2，Raz2,如图5所示。

图5 轴系误差随动状态关系图Fig.5 Relationshop diagram when axial system erroris in servo state

当方位框坐标系OXyYyZy和俯仰框坐标系OXpYpZp绕OZa2和OXy旋转的方位角和俯仰角分别为α,β时，Rax2,Ray2,Raz2变化为Rpxe,Rpye,Rpze，即表示为OXaYaZa坐标系中的向量R，因轴系误差θ和γ的存在，同样经过α,β时分别变换为Rpxe,Rpye,Rpze。根据式(1)～式(6)可得

(13)

(14)

整理后可得

(15)

在OXaYaZa坐标系中的向量R，即Rax,Ray,Raz在理想轴系和有轴系误差引起的随动误差值为

(16)

(17)

式中：I为3×3的单位矩阵，即

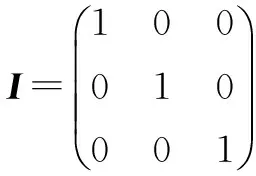
(18)

将式(6)、式(12)和式(18)代入式(17)后整理可得

(19)

在OXaYaZa坐标系中的向量R，分解到OXaYaZa坐标系中3个轴的分量分别为Rax，Ray，Raz。机载光电转塔系统的视轴一般与OYa重合或平行，在此取与OYa重合，并将向量R单位化，则有

(20)

将式(20)代入式(19)，可将式(19)简化为

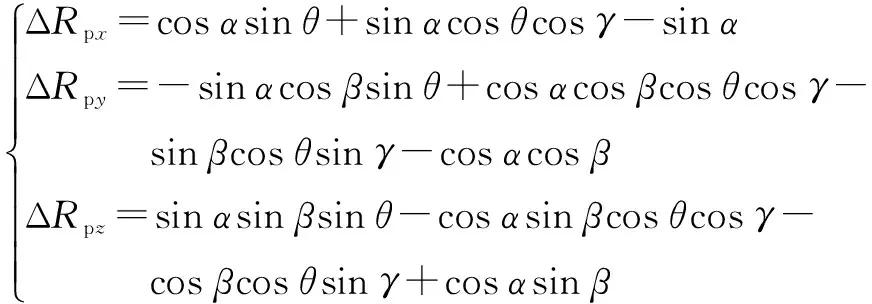
(21)

2 仿真与结果分析

由于安装与配合误差、结构变形误差、加工误差、成件误差等因素的存在，折合到输出轴不可避免会产生机载光电转塔系统在方位轴和俯仰轴的轴系误差。按照系统误差合成的原理，考虑到未定系统误差的不确定性及项数较多，采用平方根求和平均法。设机载光电转塔系统轴系在方位轴和俯仰轴的系统合成误差角度分别为θ，γ时，为了跟踪空间范围的某一个目标或监控某一个区域时，机载光电转塔系统方位和俯仰需要随动的角度分别为α，β，将式(21)中ΔRpx和ΔRpz线位移误差转换为对应的角位移误差，按照表1给出了几组合成误差和随动跟踪范围的参数算例，利用软件编程，可以得出不同轴系误差情况下在方位、俯仰和两自由度合成的误差仿真曲线，结果见图6～图8。

表1 随动角度和轴系误差参数表

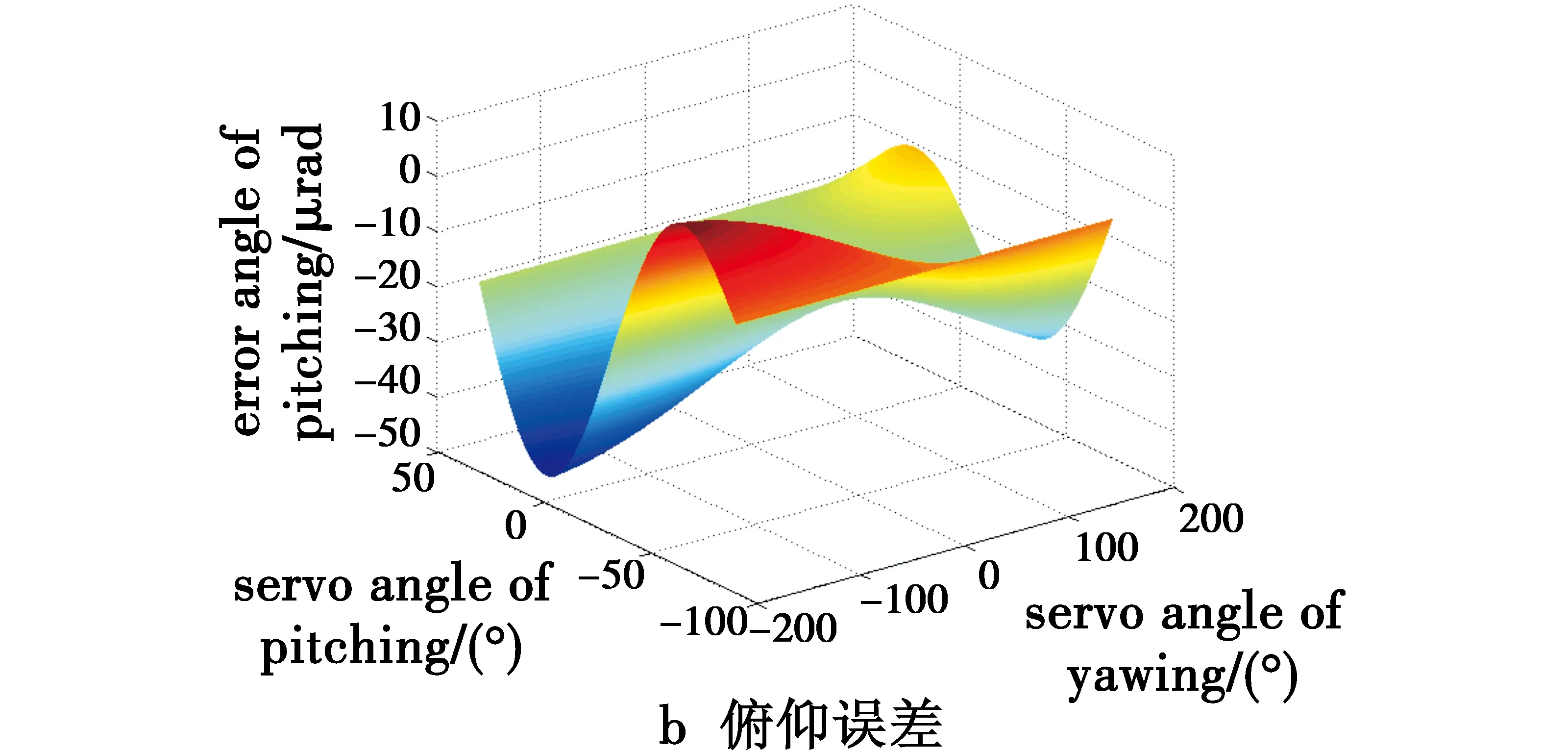
图6 轴系误差参数Ⅰ的误差曲线Fig.6 Error curves with axial system error parameter Ⅰ

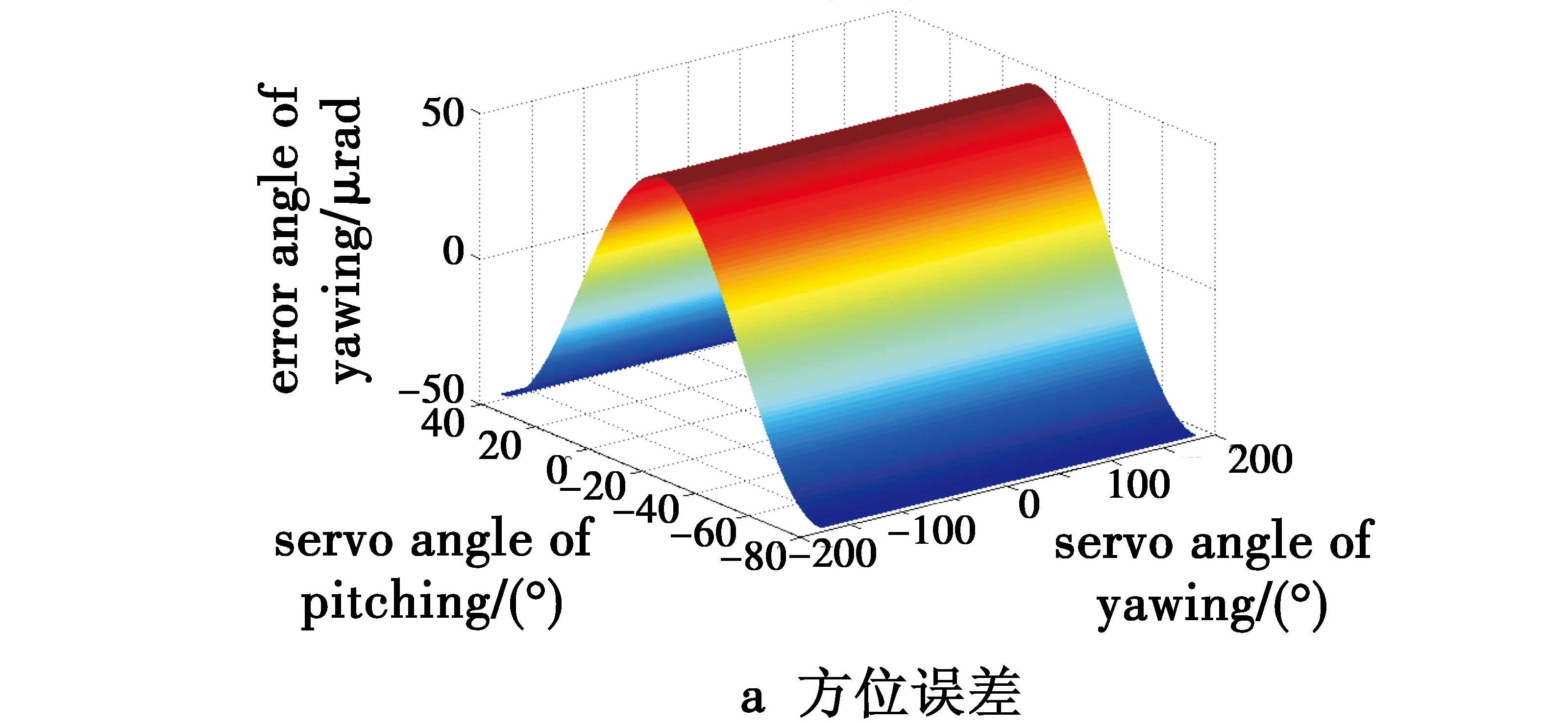
图7 轴系误差参数Ⅱ的误差曲线Fig.7 Error curves with axial system error parameter Ⅱ

当存在5″的方位轴和俯仰轴误差时，在不同的方位和俯仰随动角度跟踪下,由图6a可知，在方位随动角度为0°和俯仰随动的负向极限角度为-80°时，误差最大，绝对值约为20 μrad;由图6b可知，在俯仰随动角度为0°和方位随动极限角度为-180°时，误差最大，绝对值约为45 μrad;由图6c可知，在机载光电转塔系统探测和监控时，合成的误差最大值出现在方位角度-180°和俯仰角度+20°范围附近，其误差最大值的绝对值约为50 μrad。当分别存在10″和20″的方位轴和俯仰轴误差时，在不同的方位和俯仰随动角度跟踪下,由图7和图8可以得出，误差绝对值最大的随动角度是基本相同的，只是10″,20″的方位方向误差绝对值变大，分别约为40 μrad和80 μrad；10″,20″的俯仰方向误差绝对值变大，分别约为90 μrad和180 μrad；10″,20″的两个自由度合成误差绝对值变大，合成的误差最大值出现在方位角度-180°和俯仰角度+20°范围附近，合成误差最大的绝对值分别约为110 μrad和200 μrad。上述分析表明，在不同随动使用范围和精度要求的机载光电转塔系统中，轴系误差的存在会对不同随动跟踪位置的目标探测和监控产生不同的精度影响。因此在系统设计时，需要根据随动范围和实际精度使用的需求，按照建立的数学模型和仿真结果进行精度分配、轴系误差控制和评估，以支撑系统设计和满足使用需求。

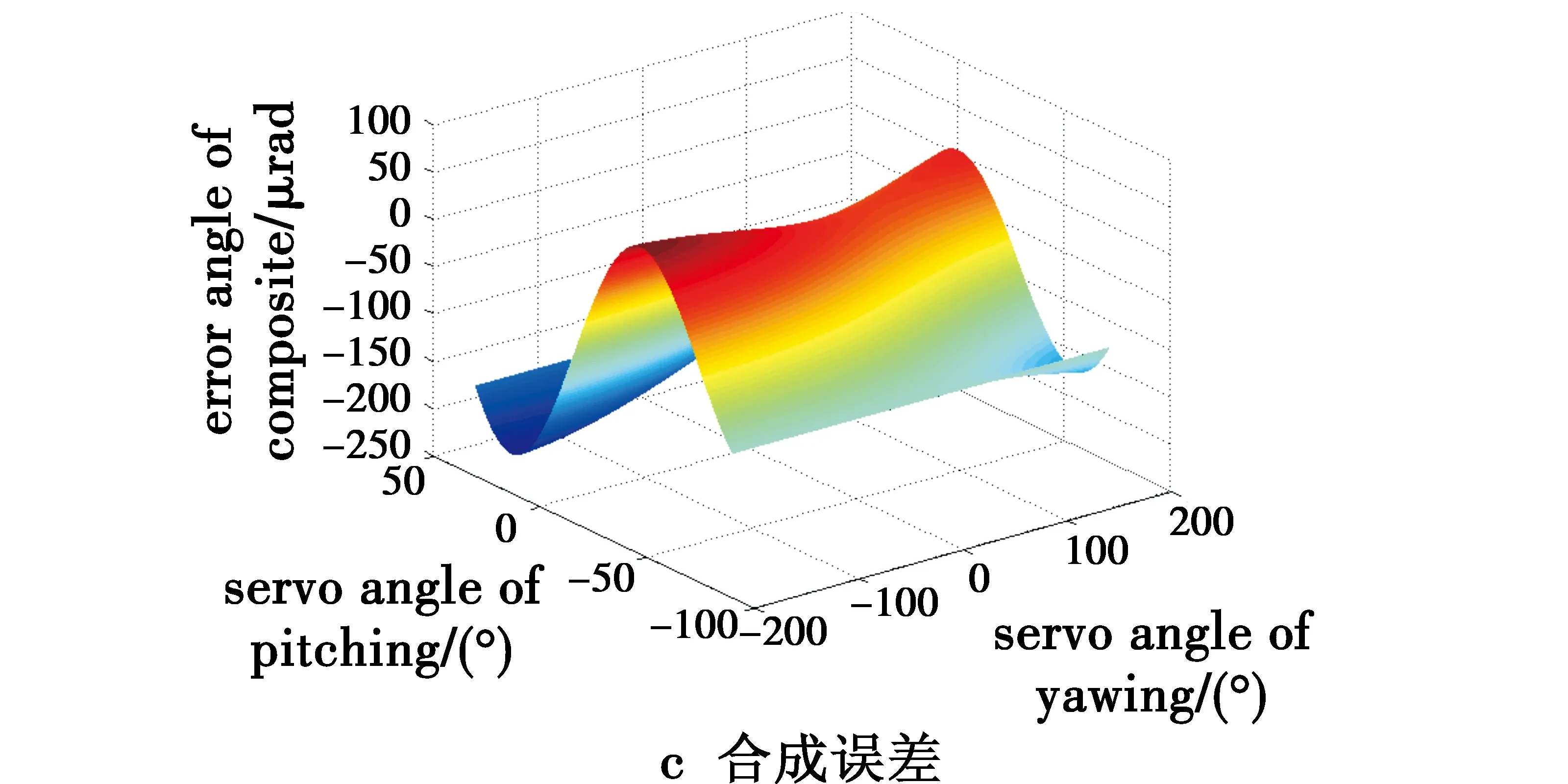
图8 轴系误差参数Ⅲ的误差曲线Fig.8 Error curves with axial system error parameter Ⅲ

在高精度的机载光电转塔系统中，加工误差、结构变形误差、配合与安装误差、成件精度等均会通过几何关系耦合到方位轴和俯仰轴，即会产生相应的轴系误差,这些误差可以通过系统设计控制和降低，但却是不可避免的存在。因此,对精度要求较高的机载光电转塔系统，就需要通过一些措施进行消除和补偿。本文建立了轴系误差数学模型，推导出因轴系误差在方位和俯仰方向随动跟踪误差公式。对特定的系统，可以通过方位轴和俯仰轴误差检测，获得轴系误差参数。在实际应用时，可以将误差角度作为位置环的补偿引入到随动控制中。当方位和俯仰随动角度变化时，补偿的值也随之实时变化，通过系统闭环控制达到实时消除误差，提高随动精度的效果。

3 结束语

机载光电转塔系统随着精密传动技术、随动控制技术、光学技术、传感器技术和图像处理技术的发展和应用,会朝着高精度和高分辨率的方向发展。为了提高精度，建立了轴系误差对随动精度影响的数学模型，推导出轴系误差在不同随动角度时对随动跟踪精度的影响关系。通过仿真对轴系误差在不同随动角度的变化特性进行了分析，给出了将误差角度反馈到随动控制系统位置环进行补偿、实时消除误差和提高精度的解决方法,可用于机载光电转塔系统设计分析和误差控制，具有工程应用参考价值。

[1] 刘洵，王国华，毛大鹏，等.军用飞机光电平台的研发趋势与技术剖析[J].中国光学与应用光学，2009,12(4):269-288.

[2] 王涛，朱明超，訚胜利，等.稳定平台轴系精度对视轴指向误差的影响分析[J].红外与激光工程，2011,40(11):2265-2269.

[3] 许照东，陈松灿，李辛.稳定平台动态精度分析及改进[J].红外与激光工程，2006,35(s1):454-458.

[4] 李岩，范大鹏.光电稳定机构指向误差建模与敏感度分析[J].国防科技大学学报，2008,30(1):104-109.

[5] 陈兆兵，郭劲，时魁，等.某复合告警系统的轴系精度分析[J].机械设计与制造，2013(3):214-216.

[6] 贾琛斐，刘建东，张健，等.舰载光电指向器多轴系耦合精度分析[J].光学与光电技术，2013,11(1):71-75.

[7] 江波，周泗忠，姜凯，等.车载经纬仪的垂轴系误差分析[J].红外与激光工程，2015,44(5):1623-1627.

[8] 张峰，丁洪生，付铁，等.星载天线指向机构误差分析与建模[J].电子机械工程，2010,26(1):41-44.

[9] 曲智勇，姚郁.仿真转台误差分析及误差建模[J].计算机仿真，2006,23(3):301-304.

[10] 贾建援，柴伟，于大林，等.方位俯仰转台误差参数辨识与指向精度分析[J].仪器仪表学报，2016,37(7):1500-1508.

[11] 叶建华，高诚辉，江吉彬.旋转台集合误差的在机测量与辨识[J].仪器仪表学报，2015,36(12):2804-2811.